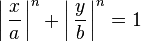Gabriel Lamé - Définition

Introduction

Gabriel Lamé
Portrait de Gabriel Lamé
Naissance	(22 juillet 1795 Tours
Décès	1er mai 1870 Paris
Profession(s)	ingénieur des mines
Formation	École Polytechnique Paris
Compléments
Mathématicien de renom Pionnier des chemins de fer

Gabriel Lamé (22 juillet 1795, Tours - 1^er mai 1870, Paris) est un mathématicien français qui apporta des contributions essentielles à la théorie des équations aux dérivées partielles par l'emploi des coordonnées curvilignes, et à la théorie mathématique de l'élasticité. Les coefficients h_i des coordonnées curvilignes sont encore actuellement dénommés "coefficients de Lamé". Ses travaux seront magistralement poursuivis par Riemann, Darboux, Poincaré et Ricci et Levi-Civita (entre autres).

Biographie

Après des études à Paris au lycée Louis-le-Grand, Lamé entre à l'École Polytechnique (X1815) puis à l'École des Mines de Paris (1818-20) comme élève-ingénieur des mines. Condisciple et ami de Clapeyron, Lamé est détaché avec lui pour Saint-Pétersbourg (1820) pour y former les élèves de l'École des voies de communications, créée en 1809 et dirigée par Augustin Bétancourt. Ils y enseignent pendant onze ans le calcul différentiel et intégral, la mécanique rationnelle, la physique, la mécanique appliquée, la physique appliquée et l'art des constructions. Le gouvernement tsariste confia en outre aux deux jeunes Français la conception de ponts suspendus.

Avec Clapeyron, Lamé rédigea un « Mémoire sur l'équilibre intérieur des solides homogènes » destiné à l'Académie des Sciences de Paris, et qui fut publié en 1833. C'est dans ce texte qu'apparaît pour la première fois la notion d'ellipsoïde des contraintes. Après les événements de juillet 1830, la tension diplomatique s'aggrava subitement entre la couronne de France et le gouvernement tsariste, et les deux ingénieurs des mines durent rentrer en France.

Trois mois après son retour, il est nommé professeur à l'École Polytechnique, succédant à César Despretz dans la chaire de physique, de 1832 à 1843 (il est ensuite examinateur jusqu'en 1862), puis à la Faculté des sciences de Paris à partir de 1851, succédant à Guillaume Libri dans la chaire de Calcul des probabilités puis Physique mathématique jusqu'en 1863, où il doit être suppléé par Marcel Verdet à cause de sa surdité.

En 1836, tout en étant toujours professeur à l'École Polytechnique, il va entrer dans la Compagnie du Chemin de fer de Paris à Saint-Germain des Frères Pereire pour participer à l'étude du tracé de la ligne de chemin de fer avec trafic voyageurs Paris-Le Pecq, avec Flachat, Clapeyron et Mony, tous Saint-Simonien. Il s'occupe plus particulièrement des machines.

Saint-Simonien convaincu, il fait partie de cette génération de polytechniciens qui, persuadés de la nécessité d'un enseignement scientifique de qualité, participeront au développement de la Physique Mathématique Rationnelle ( citons Poisson, Navier, Coriolis, Saint-Venant, Darcy, etc. ). "Ecartez à tout jamais la division de la science en mathématiques pures et en mathématiques appliquées". Dans son esquisse d'une réforme pour l'enseignement des sciences (Ed Gauthier-Villars, 1867), il définit trois "buts" : le but "rationnel" est celui d'exercer et de nourrir la faculté du raisonnement ; le but pratique est de faire connaître les formules et les règles dans les sciences d'applications ; le but "progressif" propose d'inspirer le goût de la recherche pour faire accélérer les progrès...L'influence d'un programme d'enseignement est un levier dont les gouvernements peuvent se servir pour transformer l'esprit et l'allure d'une nation : par le but pratique, elle sera active mais routinière ; par l'enseignement "progressiste", son activité sera constamment créatrice.

Lamé se fit connaître particulièrement par ses travaux sur les coordonnées curvilignes, pour lesquelles il imagina des notations toujours utilisées dans le contexte du calcul tensoriel. Parmi ces systèmes curvilignes, il y a lieu de mentionner les quadriques homofocales. La recherche des solutions de l'équation de Laplace sur des géométries particulières (cylindres, triangles, etc.) l'amena à l'étude de certaines courbes ressemblant à des ellipses, appelées maintenant courbes de Lamé :

où n est un nombre réel positif.

Lamé étudia également les modes propres et introduisit de nouvelles fonctions, comme les fonctions de Lamé dont font partie les harmoniques ellipsoidales. Les fonctions, A,B,C qu'il introduira seront analogues aux fonction elliptique de Jacobi introduites par Jacobi(1827), sn(x,k), cn(x,k) et dn(x,k). En physique mathématique, on retrouve selon les cas, l'une ou l'autre des notations. Son élève Émile Mathieu, poursuivant ce travail, décrira l'équation de Mathieu.

Lamé est aussi connu pour son analyse de la complexité algorithmique de l'algorithme d'Euclide. En utilisant la suite de Fibonacci, il a démontré que cet algorithme trouve le PGCD des entiers a et b en moins de 5k étapes, où k est le nombre de chiffres décimaux de b. Il a aussi obtenu un cas particulier (n=7) du dernier théorème de Fermat. Il pensait avoir obtenu une preuve complète, mais il se trompait.

Gabriel Lamé était l'oncle du physicien Alfred Potier. Sa fille épousa Michel-Eugène Lefébure de Fourcy.