Géométrie - Définition

Géométrie classique

Pour Henri Poincaré, l’espace géométrique possède les propriétés suivantes:

1. Il est continu
2. Il est infini
3. Il a trois dimensions
4. Il est homogène, c’est-à-dire que tous ses points sont identiques entre eux
5. Il est isotrope, c’est-à-dire que toutes les droites qui passent par un même point sont identiques entre elles.

Les géométries euclidienne et non euclidienne correspondent à cette définition stricto sensu de l'espace. Construire une telle géométrie consiste à énoncer les règles d'agencement des quatre objets fondamentaux le point, la droite, le plan et l'espace. Ce travail reste l'apanage de la géométrie pure qui est la seule à travailler ex nihilo.

Géométrie plane

La géométrie plane repose d'abord sur une axiomatique qui définit l'espace ; puis sur des méthodes d'intersections, de transformations et de constructions de figures (triangle, parallélogramme, cercle, sphère, etc.).

La géométrie projective est la plus minimaliste, ce qui en fait un tronc commun pour les autres géométries. Elle est fondée sur des axiomes

1. d'incidence (ou d'appartenance) dont la caractéristique la plus notable (et la plus singulière) est : « Deux droites coplanaires possèdent un unique point commun. »
2. d'ordre : permet notamment d'ordonner les points d'une droite. De ce point de vue, une droite projective s'apparente à un cercle car deux points définissent deux segments.
3. de continuité : Ainsi, dans tout espace géométrique, l'on peut joindre un point à un autre par un cheminement continu. En géométrie euclidienne, cette axiome est l'axiome d'Archimède.

Parallélisme 

Distinguer dans la géométrie projective des éléments impropres caractérise la géométrie arguésienne. Puis la géométrie affine nait de l'élimination de ces éléments impropres. Cette suppression de points crèe la notion de parallélisme puisque désormais certaines paires de droites coplanaires cessent d'intersecter. Le point impropre supprimé est assimilable à la direction ces droites. De plus, deux points ne définissent plus qu'un segment (celui des deux qui ne contient pas le point impropre) et rend familière la notion de sens ou orientation (c'est-à-dire, cela permet de distinguer de ).

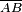
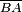
Congruence 

Géométries euclidienne et non-euclidiennes

Le cinquième axiome ou « postulat de parallèles » de la géométrie d'Euclide fonde la géométrie euclidienne :

Par un point extérieur à une droite, il passe toujours une parallèle à cette droite, et une seule.

Voir l'axiomatique de Hilbert ou les Éléments d'Euclide pour des énoncés plus complet de la géométrie euclidienne.

La réfutation de ce postulat à conduit à l'élaboration de deux géométries non euclidiennes : la géométrie hyperbolique par Gauss, Lobatchevski, Bolyai et la géométrie elliptique par Riemann.

Géométrie analytique

La géométrie analytique est la plus familière. Elle repose sur le principe de base que toute droite est assimilable à une représentation (une image) de l'ensemble des réels (ou plus largement, d'un corps. L'espace est alors décomposable en sous-espaces et un point est définissable par des coordonnées. Il s'ensuit que toute figure est déterminée par un système d'équations et/ou d'inéquations. Par exemple, une courbe est la représentation d'une fonction. L'on voit ainsi que cette approche, issue de l'algèbre linéaire et basée sur la notion d'espace vectoriel, est à un pont entre la géométrie et l'analyse.

Cette géométrique est conforme à la géométrie pure dans le sens où l'espace vectoriel permet de construire des modèles de géométries (en tant qu'objets mathématiques).

Programme d'Erlangen

Dans la conception de Felix Klein (auteur de programme d'Erlangen), la géométrie est l'étude des espaces de points sur lesquels opèrent des groupes de transformations (appelées aussi symétries) et des quantités et des propriétés qui sont invariantes pour ces groupes.

Parmi les transformations les plus connues, on retrouve les isométries, les similitudes, les rotations, les réflexions, les translations et les homothéties.

Il ne s'agit donc pas d'une discipline mais d'un important travail de synthèse qui a permis une vision claire des particularités de chaque géométrie. Ce programme caractérise donc plus la géométrie qu'il ne la fonde. Il eut un rôle médiateur dans le débat sur la nature des géométries non-euclidiennes et la controverse entre géométries analytique et synthétique.

Géométrie des groupes classiques

Il y a en géométrie différentielle et en géométrie algébrique des groupes de Lie et des groupes algébriques, qui eux on des espaces homogènes, et la géométrie classique se remène souvent à l'étude des ces espaces homogènes. Les géométries affine et projective sont liées aux groupes linéaires, et les géométries euclidienne, sphérique, elliptique et hyperbolique sont liées aux groupes orthogonaux.

Lorsqu'il y a des classifications explicites des groupes de Lie ou algébriques ou des leurs espaces homogènes vérifiant certaines hypothèses (groupes de Lie ou algébriques simples, espaces symétriques, variétés de drapeaux généralisées, espaces de courbure constante, par exemples), les principaux éléments de ces classifications sont parfois issus de la géométrie classique, et les groupes auxquels sont associés ses géométrie classique sont liés aux groupes dits classiques (groupes linéaires, orthogonaux, symplectiques, par exemples).

La plupart des géométries classiques sont liées aux groupes de Lie ou algébriques simples, dit classiques (ils sont issus de l'algèbre linéaire). Il y d'autres groupes de Lie ou algébriques simples, et ils sont dits « exceptionnels » et ils donnent lieu à la géométrie exceptionnelle, avec certaines analogies avec la géométrie classique. Cette distiction est due au fait que les groupes simple sont (sous certaines hypothèses) classés en plusieurs séries infinies (souvent quatre) et en un nombre fini d'autres groupes (souvent cinq), et c'est ces derniers groupes qui sont exceptionnels, et ils ne relèvent pas de l'algèbre linéaire (du moins pas de la même manière): ils sont souvent liés à des structures algébriques non associatives (algèbres d'octonions, algèbres de Jordan exceptionnelles, par exemple).

Aux groupes de Lie ou algébriques simples sont associés des diagrammes de Dynkin (des sortes de graphes), et certaines propriétés de ces géométries peuvent se lirent dans ces diagrammes.