Géométrie - Définition
La liste des auteurs de cet article est disponible ici.
Applications de la géométrie
Longtemps, géométrie et astronomie ont été liées. À un niveau élémentaire, le calcul des tailles de la lune, du Soleil et de leurs distances respectives à la Terre fait appel au théorème de Thalès. Dans les premiers modèles du système solaire, à chaque planète était associé un solide platonicien. Depuis les observations astronomiques de Kepler, confirmées par les travaux de Newton, il est prouvé que les planètes suivent une orbite elliptique dont le Soleil constitue un des foyers. De telles considérations de nature géométrique peuvent intervenir couramment en mécanique classique pour décrire qualitativement les trajectoires.
En ce sens, la géométrie intervient en ingénierie dans l'étude de la stabilité d'un système mécanique. Mais elle intervient encore plus naturellement dans le dessin industriel. Le dessin industriel montre les coupes ou les projections d'un objet tridimensionnel, et est annoté des longueurs et angles. C'est la première étape de la mise en place d'un projet de conception industrielle. Récemment, le mariage de la géométrie avec l'informatique a permis l'arrivée de la conception assistée par ordinateur (CAO), des calculs par éléments finis et de l'infographie.
La trigonométrie euclidienne intervient en optique pour traiter par exemple de la diffraction de la lumière. Elle est également à l'origine du développement de la navigation : navigation maritime aux étoiles (avec les sextants), cartographie, navigation aérienne (pilotage aux instruments à partir des signaux des balises).
Les nouvelles avancées en géométrie au XIXe siècle trouvent des échos en physique. Il est souvent dit que la géométrie riemannienne a été initialement motivée par les interrogations de Gauss sur la cartographie de la Terre. Elle rend compte en particulier de la géométrie des surfaces dans l'espace. Une de ses extensions, la géométrie lorentzienne, a fourni le formalisme idéal pour formuler les lois de la relativité générale. La géométrie différentielle trouve de nouvelles applications dans la physique post-newtonienne avec la théorie des cordes ou des membranes.
La géométrie non commutative, inventée par Alain Connes, tend à s'imposer pour présenter les bonnes structures mathématiques avec lesquelles travailler pour mettre en place de nouvelles théories physiques.
Domaines de recherche relevant de la géométrie
Géométrie riemannienne
La géométrie riemannienne peut être vue comme une extension de la géométrie euclidienne. Son étude porte sur les propriétés géométriques d'espaces (variétés) présentant une notion de vecteurs tangents, et équipés d'une métrique (métrique riemannienne) permettant de mesurer ces vecteurs. Les premiers exemples rencontrés sont les surfaces de l'espace euclidien de dimension 3 dont les propriétés métriques ont été étudiées par Gauss dans les années 1820. Le produit euclidien induit une métrique sur la surface étudiée par restriction aux différents plans tangents. La définition intrinsèque de métrique fut formalisée en dimension supérieure par Riemann. La notion de transport parallèle autorise la comparaison des espaces tangents en deux points distincts de la variété : elle vise à transporter de manière cohérente un vecteur le long d'une courbe tracée sur la variété riemannienne. La courbure d'une variété riemannienne mesure par définition la dépendance éventuelle du transport parallèle d'un point à un autre par rapport à la courbe les reliant.
La métrique donne lieu à la définition de la longueur des courbes, d'où dérive la définition de la distance riemannienne. Mais les propriétés métriques des triangles peuvent différer de la trigonométrie euclidienne. Cette différence est en partie étudiée à travers le théorème de comparaison de Toponogov, qui permet de comparer du moins localement la variété riemannienne étudiée à des espaces modèles, selon des inégalités supposées connues sur la courbure sectionnelle. Parmi les espaces modèles :
- L'espace euclidien est une variété riemannienne de courbure nulle ;
- La sphère de dimension n sont une variété riemannienne de courbure positive constante 1 ;
- L'espace hyperbolique de dimension n est une variété riemannienne de courbure négative -1.
Géométrie complexe
La géométrie complexe porte sur les propriétés d'espaces pouvant localement s'identifier à 
. Ces objets (variété complexe) présentent une certaine rigidité, découlant de l'unicité d'un prolongement analytique d'une fonction à plusieurs variables.
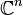
Géométries symplectique et de contact
La géométrie symplectique est une branche de la géométrie différentielle et peut être introduite comme une généralisation en dimension supérieure de la notion d'aire orientées rencontrée en dimension 2. Elle est liée aux formes bilinéaires alternées. Les objets de cette géométrie sont les variétés symplectiques, qui sont des variétés différentielles munie d'un champs de formes bilinéaires alternées. Par exemple, un espace affine attaché à un espace vectoriel muni d'une forme bilinéaire alternée non dégénérée est une variété symplectique.
La géométrie de contact est une branche de la géométrie différentielle qui étudie les variétés de contact, qui sont des variétés différentielles munies d'un champs d'hyperplans des espaces tangents vérifiant certaines propriétés. Par exemple, l'espace projectif déduit un espace vectoriel muni d'une forme bilinéaire alternée non dégénérée est une variété de contact.