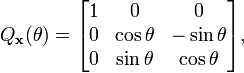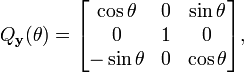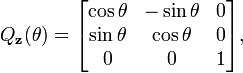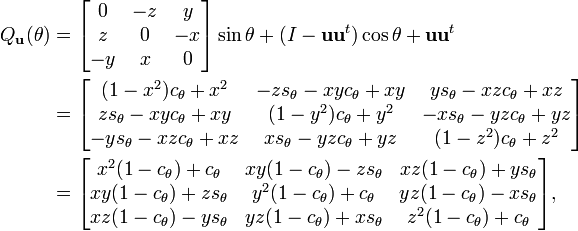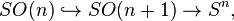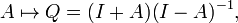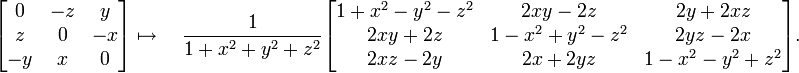Matrice de rotation - Définition
La liste des auteurs de cet article est disponible ici.
Multiplication
L'inverse d'une matrice de rotation est sa transposée, qui est aussi une matrice de rotation :
Le produit de deux matrices de rotation est une matrice de rotation :
Pour n plus grand que 2, la multiplication de matrices de rotation n×n n'est pas commutative.
Remarquant que toute matrice unité est une matrice de rotation, et que la multiplication des matrices est associative, on peut résumer ces propriétés en disant que les matrices de rotation n×n forment un groupe, qui pour n > 2 est non abélien. Appelé le groupe spécial orthogonal, et noté SO(n), SO(n, R), SOn, ou SOn(R), le groupe des matrices de rotation n×n est isomorphe au groupe des rotations d'un espace à n dimensions, ce qui veut dire. que la multiplication des matrices de rotation correspond à la composition des rotations, appliquée dans le même ordre (de la gauche vers la droite) que celui des matrices correspondantes.
Exemples
|
|
Décompositions
Plans indépendants
Considérons la matrice de rotation 3×3
Si, dans une certaine direction v, Q agit comme une multiplication par un facteur λ (autrement dit si v est un vecteur propre, de valeur propre associée λ), nous aurons
donc
Ainsi λ est une racine du polynôme caractéristique de Q,
On remarquera deux propriétés importantes. D'une part, l'une des racines est 1, ce qui nous dit qu'une certaine direction est laissée fixe par la matrice. Pour les rotations en trois dimensions, c'est l'axe de la rotation (un concept qui se généralise uniquement aux dimensions impaires). D'autre part, les deux autres racines sont complexes conjuguées, de produit 1 (le terme constant du polynôme du second degré), et dont la somme est 2 cos θ (l'opposé du terme de degré 1). Le même phénomène se produit pour toutes les matrices de rotation 3×3 (avec deux cas particuliers : pour une rotation nulle les "valeurs complexes conjuguées " valent en fait toutes deux 1, et pour une rotation de 180°, toutes deux valent −1). En fait, une factorisation analogue existe pour n'importe quelle matrice de rotation n×n. Si la dimension, n, est impaire, il y aura une valeur propre supplémentaire valant 1, et en toute dimension le reste du polynôme se factorisera en termes du second degré comme celui que nous avons vu (avec les deux cas particuliers déjà mentionnés). Le polynôme caractéristique sera toujours de degré n ; il y aura donc n valeurs propres ; et comme une matrice de rotation commute toujours avec sa transposée, c'est une matrice normale, et elle peut donc être diagonalisée. En conclusion, toute matrice de rotation, exprimée dans une base convenable, se décompose en rotations indépendantes de sous-espaces de dimension 2 (des plans vectoriels); au plus n⁄2 d'entre eux.
La somme des termes de la diagonale principale d'une matrice est appelée sa trace; elle ne dépend pas de la base, et vaut toujours la somme des valeurs propres. Cela a l'intéressante conséquence pratique de donner directement l'angle de rotation θ (dans un (sous)-espace de dimension 2) pour les matrices de rotation 2×2 et 3×3 : pour une matrice 2×2 la trace est 2 cos(θ) (ce qui est en fait évident, comme on va le voir), et pour une matrice 3×3 , elle vaut 1+2 cos(θ). En dimension 3, le sous-espace est formé des vecteurs orthogonaux à l'axe de rotation (la direction propre de valeur propre 1). Ainsi, à partir de n'importe quelle matrice de rotation 3×3, nous pouvons déterminer un axe et un angle, et ceux-ci déterminent complètement la rotation (à l'orientation près).
Suites d'angles
Une matrice de rotation 2×2 a nécessairement la forme suivante :
avec a2+b2 = 1. Nous pouvons donc poser a = cos θ et b = sin θ, pour un certain angle θ. Pour déterminer θ, il ne suffit pas de connaître a ou b seulement ; nous devons utiliser les deux nombres pour obtenir le quadrant correct, à l'aide d'une fonction arctangente à deux variables (notée atan2 dans beaucoup de langages de programmation).
Considérons à présent la première colonne d'une matrice de rotation 3×3,
Bien que a2+b2 ne soit pas en général égal à 1, mais à une certaine valeur r2 < 1, nous pouvons utiliser une variante du calcul précédent pour obtenir ce qu'on appelle une rotation de Givens, transformant la colonne en
annulant le coefficient b. Cette rotation agit sur le plan des axes x et y. Nous pouvons ensuite recommencer dans le plan xz, pour annuler c. Opérant sur la matrice entière, ces deux rotations la mettent sous la forme.
Nous intéressant à présent à la deuxième colonne, une rotation de Givens dans le plan yz permet d'annuler la valeur z. La matrice complète devient alors
c'est-à-dire la matrice identité. Ainsi, nous avons décomposé Q en
Une matrice de rotation n×n aura (n−1)+(n−2)+⋯+2+1 = n(n-1)/2 termes en dessous de la diagonale qui devront être annulés. Cela peut se faire en généralisant la même idée, parcourant les colonnes avec une série de rotations dans une succession de plans. On en déduit que l'ensemble des matrices de rotation n×n, qui ont chacune n2 termes, peut être paramétré par n(n−1)/2 angles.
| xzxw | xzyw | xyxw | xyzw |
| yxyw | yxzw | yzyw | yzxw |
| zyzw | zyxw | zxzw | zxyw |
| xzxb | yzxb | xyxb | zyxb |
| yxyb | zxyb | yzyb | xzyb |
| zyzb | xyzb | zxzb | yxzb |
En trois dimensions, cela reformule dans le langage des matrices une observation faite par Euler, aussi les mathématiciens appellent-ils les trois angles obtenus des angles d'Euler. Cependant, la situation est un peu plus compliquée que ce que nous avons vu jusqu'ici : en dépit du petit nombre de dimensions, nous avons un choix considérable de séquences de paires d'axes, et aussi une certaine liberté dans le choix des angles. Ainsi, de nombreuses conventions différentes sont employées pour paramétrer les rotations tridimensionnelles en physique, en médecine, en chimie, ou dans d'autres disciplines. En tenant compte de la possibilité de prendre des repères fixes ou mobiles, 24 séquences différentes sont possibles. Et alors que certaines disciplines appellent toutes ces séquences des angles d'Euler, d'autres donnent des noms différents (Euler, Cardan, Tait-Byan, lacet-roulis-tangage) à des séquences différentes.
Une des raisons de ce grand nombre d'options est que, comme remarqué précédemment, les rotations en trois dimensions (et plus) ne commutent pas. Si nous permutons une suite donnée de rotations, nous n'obtenons pas (en général) le même résultat. Cela a également pour conséquence que nous ne pouvons pas composer des rotations (d'axes distincts) en additionnant leurs angles. Ainsi, les angles d'Euler ne sont pas des vecteurs, en dépit d'une ressemblance superficielle en tant que triplets de nombres.
Dimensions emboîtées
Une matrice de rotation 3×3 telle que
donne l'impression qu'une matrice de rotation 2×2,
est incrite dans le coin supérieur gauche:
Ce n'est pas une illusion ; on trouve de nombreuses copies de rotations n-dimensionnelles au sein des rotations (n+1)-dimensionnelles, en tant que sous-groupes. Chaque plongement laisse une direction fixe, qui dans le cas des matrices 3×3 est l'axe de rotation. Par exemple, nous avons
fixant respectivement l'axe des x, l'axe des y et l'axe des z. L'axe de rotation n'a pas besoin d'être un axe de coordonnées ; si u = (x, y, z) est un vecteur unité de la direction souhaitée, alors
où cθ = cos θ, sθ = sin θ, est une rotation d'angle θ laissant l'axe u fixé.
Une direction dans l'espace à (n+1) dimensions sera un vecteur unité, que l'on peut considérer comme un point sur une sphère généralisée, Sn. Il est ainsi naturel de décrire le groupe des rotations SO(n+1) come composé de SO(n) et de Sn. Un formalisme adapté est celui des espaces fibrés,
où pour chaque direction dans l'« espace de base », Sn, la « fibre » au-dessus d'elle dans l'« espace total », SO(n+1), est une copie de SO(n), représentant les rotations qui gardent cette direction fixée.
Nous pouvons ainsi construire une matrice de rotation n×n en partant d'une matrice 2×2, plaçant un axe de rotation sur S2 (la sphère ordinaire de l'espace à trois dimensions), orientant la rotation résultante en ajoutant un axe de rotation sur S3, et ainsi de suite jusqu'à Sn−1. Un point sur Sn possède n « coordonnées sphériques » (en d'autres termes, Sn est une variété de dimension n), ainsi nous avons à nouveau besoin de n(n−1)/2 nombres pour décrire toutes les matrices de rotation n×n.
En fait, la décomposition angulaire séquentielle discutée précédemment peut être vue comme le même processus dans l'autre sens. La composition des n−1 rotations de Givens amène la première colonne (et la première ligne) à (1,0,…, 0), et le reste de la matrice est une matrice de rotation ayant une dimension de moins, plongée de telle sorte que (1,0,…, 0) reste fixé.
Paramétrages antisymétriques
Quand Q, une matrice de rotation n×n, n'admet pas −1 comme valeur propre, et donc qu'aucune des rotations planes qui la composent n'est une rotation de 180°, Q+I est une matrice inversible. C'est le cas de presque toutes les matrices de rotation, et on peut alors montrer que (Q−I)(Q+I)−1 est une matrice antisymétrique, A. Ainsi, AT = −A; comme la diagonale de A est nécessairement nulle, et que les termes du triangle supérieur déterminent les autres , A contient n(n−1)/2 coefficients indépendants. Heureusement, I−A est inversible si A est antisymétrique ; ainsi nous pouvons retrouver la matrice initiale Q à l'aide de la transformation de Cayley :
qui envoie n'importe quelle matrice antisymétrique A vers une matrice de rotation. En fait, en dehors des exceptions déjà mentionnées, on peut produire n'importe quelle matrice de rotation de cette manière. Bien que pour des applications pratiques, on puisse rarement se permettre de négliger le cas des rotations de 180°, la transformation de Cayley reste un outil utile, donnant une paramétrisation n'utilisant pas les fonctions trigonométriques de la plupart des matrices de rotation.
En trois dimensions, par exemple, nous avons
Si nous notons les termes antisymétriques comme un vecteur, v= (x, y, z), ceci construit une rotation de 90° autour de l'axe des x pour v=(1,0,0), autour de l'axe des y pour v=(0,1,0), et autour de l'axe des z pour v=(0,0,1). Les rotations de 180° sont tout juste inatteignables, car, à la limite quand x tend vers l'infini, la matrice correspondant à v=(x, 0,0) tend vers une rotation de 180° autour de l'axe des x, et il en va de même dans les autres directions.
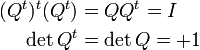
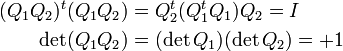
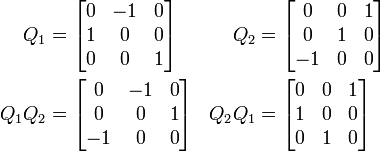
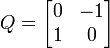
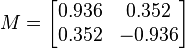
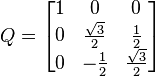
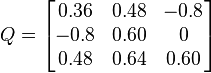
![\overrightarrow u\begin{pmatrix} -\frac{1}{3} \\[3pt] \frac{2}{3} \\[3pt] \frac{2}{3} \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/2/2c6eca6c05480410e375da5093131aca_d43f0bffd1b8b69145ad3876fb63cf40.png)
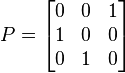
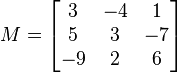
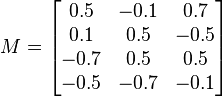
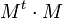
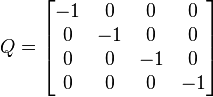
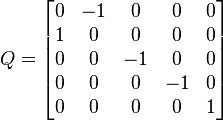
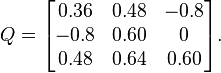
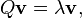
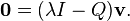
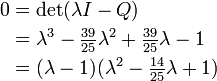
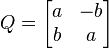
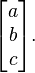
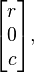
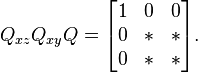
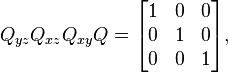
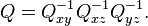
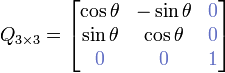
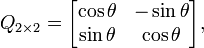
![Q_{3 \times 3} = \left[ \begin{matrix} Q_{2 \times 2} & \bold{0} \\ \bold{0}^t & 1 \end{matrix} \right] .](https://static.techno-science.net/illustration/Definitions/autres/7/759b6679e6cf3f98beddd0fc6b85e08f_d5b6f73087097924e9694a7ff8d2c11b.png)