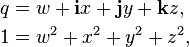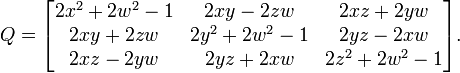Matrice de rotation - Définition
La liste des auteurs de cet article est disponible ici.
Ambigüités de la représentation matricielle
L'interprétation d'une matrice de rotation peut donner naissance à plusieurs ambigüités :
- Changement de repère ou déplacement
- La modification des coordonnées d'un vecteur peut correspondre à une rotation de ce vecteur (alibi), ou à une rotation du repère (alias).
- Repère direct ou inverse
- La matrice peut représenter la rotation dans un repère orienté positivement ou négativement.
- Référentiel fixe ou mobile
- Les axes de coordonnées peuvent être fixés ou tourner avec un solide.
- Vecteurs ou formes linéaires
- L' espace vectoriel admet un espace dual constitué des formes linéaires sur cet espace, et la matrice peut agir sur les vecteurs ou sur les formes
Dans la plupart des cas, l'autre interprétation correspondrait à la matrice transposée (donc inverse).
Rotations infinitésimales
Les matrices de l'algèbre de Lie ne sont pas elles-mêmes des rotations ; ces matrices antisymétriques sont des dérivées, proportionnelles à des différences de rotations. Une véritable "rotation différentielle", ou encore une matrice de rotation infinitésimale a la forme
où dθ est infiniment petit. Ces matrices n'ont pas toutes les propriétés des matrices de rotation (finies) usuelles. Pour le comprendre, considérons
La condition d'orthogonalité, QtQ = I n'est pas vérifiée, puisque le produit
diffère de la matrice unité par des infiniments petits du second ordre ; nous les négligeons donc, et nous dirons qu'au premier ordre, une matrice infinitésimale de rotation est orthogonale. Regardonc à présent le carré de la matrice
Négligeant à nouveau les termes du second ordre, nous voyons que l'angle a simplement doublé. La différence principale de comportement, nous demandera une seconde rotation infinitésimale,
Comparons les produits dAxdAy et dAydAx.
Comme dθ dφ est du second ordre, nous le négligeons; ainsi, au premier ordre, la multiplication des matrices de rotation infinitésimales est commutative. En fait,
toujours au premier ordre.
Il faut donc toujours soigneusement distinguer (le traitement au premier ordre de) ces matrices infinitésimales à la fois des matrices de rotation finies, et des dérivées de ces matrices (qui sont antisymétriques). Ainsi, le comportement des matrices finies dans la formule BCH contraste avec celui des matrices infinitésimales, car tous les termes des commutateurs seront des infiniments petits du second ordre, et donc ces matrices formeront bien un espace vectoriel dans ce cas.
Topologie du groupe des rotations : théorie de Lie
Groupes de Lie
On a vu que les matrices de rotation n×n forment un groupe, le groupe spécial orthogonal, SO(n). Cette structure algébrique se double d'une structure topologique, car les opérations de multiplication et d'inversion (qui ici est simplement la transposition) sont des fonctions continues des coefficients des matrices. Ainsi SO(n)est un exemple classique de groupe topologique (d'un point de vue purement topologique, c'est une variété compacte). De plus, les opérations sont non seulement continues, mais lisses (de classe
La plupart des propriétés des matrices de rotation dépendent fort peu de la dimension n; mais envisagé comme un groupe de Lie, on rencontre une différence systématique entre les dimensions paires et impaires. De plus, pour les petites valeurs de n, certaines irrégularités se produisent ; par exemple, contrairement au cas général, SO(4) n'est pas un groupe de Lie simple, mais est isomorphe au produit direct de S3 et de SO(3).
Algèbres de Lie
Associé à chaque groupe de Lie, on définit une algèbre de Lie, un espace vectoriel muni d'une forme bilinéaire alternée appelée un crochet (de Lie). L'algèbre correspondant à SO(n) est notée
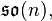
Pour les matrices de rotation 2×2, l'algèbre de Lie est une droite vectorielle, formée des multiples de
Dans ce cas, le crochet est toujours nul, ce qui nous dit qu'en dimension 2, les rotations commutent. Ce n'est pas le cas en dimensions supérieures. Ainsi, pour les matrices de rotation 3×3, nous obtenons un espace de dimension 3 pour lequel une base commode (de générateurs) est
Le crochet étant
On peut naturellement identifier chaque matrice de cette algèbre de Lie avec un vecteur de R3,
Avec cette identification, le crochet de SO(3) s'identifie au produit vectoriel,
De même, la correspondance entre une matrice et le vecteur v qui la représente correspond à
-
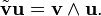
ce qui implique que v est dans le noyau de l'endomorphisme associé à la matrice avec laquelle on l'a identifié, puisque v
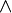
L'application exponentielle
L'application exponentielle relie l'algèbre de Lie au groupe de Lie ; on la définit à l'aide de la série entière bien connue pour ex:
Pour toute matrice antisymétrique A, exp(A) est toujours une matrice de rotation.
Un important exemple pratique est le cas 3×3, où nous venons de voir qu'on peut identifier chaque matrice antisymétrique avec un vecteur ω = uθ, où u = (x, y, z) est un vecteur unitaire. Rappelons que u est dans le noyau de la matrice associée à ω, et donc que si l'on utilise une base dont u est l'axe des z, la dernière ligne et la dernière colonne seront nulles. Nous savons ainsi déjà que la matrice exponentielle laisse u fixé. Il n'est pas réellement possible de donner une formule pour une telle base en fonction de u (l'existence d'une formule continue contredirait le théorème de la boule chevelue), mais on peut exponentier directement dans la base initiale, obtenant
où c = cos θ⁄2, s = sin θ⁄2. On reconnait la matrice d'une rotation d'angle θ autour de l'axe u. Il faut remarquer également que cette transformation de matrices antisymétriques est tout à fait distincte de la ransformation de Cayley discutée plus haut.
Quelle que soit la dimension, si nous choisissons une matrice non nulle A et considérons ses multiples (tA, où t est un scalaire), l'exponentiation donne une famille de matrices de rotation etA situées le long d'une géodésique du groupe de Lie (en tant que variété), formant un sous-groupe à un paramètre. Plus généralement, l'exponentielle est un homéomorphisme entre un voisinage de 0 dans l'algèbre de Lie et un voisinage de l'identité du groupe de Lie. En fait, on peut construire n'importe quelle matrice de rotation comme exponentielle d'une matrice antisymétrique, donc pour ces groupes l'application exponentielle est une surjection.
La formule de Baker–Campbell–Hausdorff
Soit deux matrices A et B de l'algèbre de Lie. Leurs exponentielles, exp(A) et exp(B), sont des matrices de rotation, que nous pouvons multiplier. Comme l'application exponentielle est surjective, nous savons qu'il existe C dans l'algèbre de Lie telle que exp(A)exp(B) = exp(C), ce que nous noterons
Quand exp(A) and exp(B) commutent (ce qui est toujours le cas pour les matrices 2×2, mais pas en général en dimension supérieure ), on a C =A+B, comme pour l'exponentiation commplexe. Le cas général est donné par la formule de Baker–Campbell–Hausdorff (dite formule BCH), un développement en série en termes de crochets, qui pour des matrices sont les commutateurs, détectant le défaut de commutativité de la multiplication. La formule générale est assez complexe, mais dans le cas des matrices, elle se simplifie en
 , dont les premiers termes peuvent aussi s'écrire
, dont les premiers termes peuvent aussi s'écrire
La représentation d'une matrice de rotation par sa décomposition angulaire, comme dans le cas des angles d'Euler, peut amener à la tentation de considérer les rotations comme formant un espace vectoriel, mais la présencec des termes d'ordre supérieur dans la formule BCH montre que cela serait une erreur.
Revenons au cas 3×3, où [A, B] est égal au produit vectoriel,
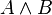
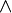
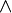
Le groupe Spin
Le groupe de Lie des matrices de rotation n×n, SO(n), est une variété compacte et connexe par arcs. Mais il n'est pas simplement connexe, aussi la théorie de Lie nous dit que c'est l'« ombre » (l'image par une application continue) d'un groupe de revêtement universel. Le groupe de revêtement, qui dans ce cas est le groupe Spin (ou groupe de spins, ou groupe des spineurs), noté Spin(n), est en général plus simple et il est plus naturel de s'y placer.
Dans le cas des rotations planes, SO(2) est topologiquement un cercle, la sphère S1. Son groupe de revêtement universel, Spin(2), est isomorphe à la droite réelle, R, munie de l'addition. En d'autres termes, chaque fois que nous utilisons des angles de valeur arbitraire, ce que nous faisons souvent, nous profitons de la simplicité des nombres réels, dont les angles sont les « ombres ». Toute matrice de rotation 2×2 correspond à une infinité dénombrable d'angles, séparés par des multiples entiers de 2π ; cela correspond à ce que le groupe fondamental de SO(2) est isomorphe aux entiers relatifs, Z.
Dans le cas des rotations de l'espace, SO(3) est topologiquement équivalent à l'espace projectif réel de dimension 3, P3(R). Son revêtement universel, Spin(3), est isomorphe à la 3-sphère, S3 ; et chaque matrice de rotation 3×3 correspond à deux points opposés de la sphère. Par conséquent, le groupe fondamental de SO(3) est isomorphe au groupe à deux éléments, Z2. Nous pouvons aussi décrire Spin(3) comme isomorphe au groupe multiplicatif des quaternions de norme 1, ou à un certain ensemble de matrices réelles 4×4, ou de matrices complexes 2×2.
Concrètement, un quaternion unité, q, avec
correspond à la matrice de rotation
C'est notre troisième version de cette matrice, ici représentant une rotation d'angle 2θ autour du vecteur non-unitaire (x, y, z), où cos θ = w et |sin θ| = ||(x, y, z)|| (le signe de sin θ dépend des signes des composantes de l'axe).
En dimension supérieure, beaucoup des propriéés de ce cas se généralisent. Les recouvrements ont tous une fibre de deux éléments, et SO(n), n > 2, a toujours pour groupe fondamental Z2. Le cadre naturel pour étudier ces groupes est celui des algèbres de Clifford. Et l'action des rotations est donnée par une sorte de "sandwich", noté qvq∗.
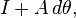
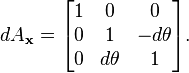
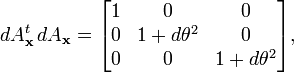
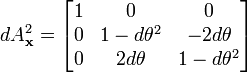
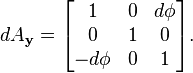
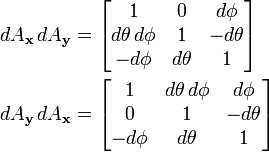
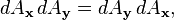
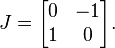
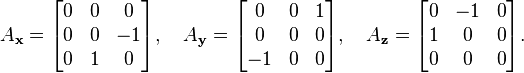
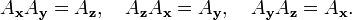
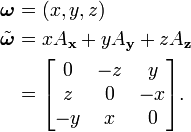
![[\tilde{\bold{u}},\tilde{\bold{v}}] = (\bold{u} \wedge \bold{v})^{\sim} . \,\!](https://static.techno-science.net/illustration/Definitions/autres/7/793dde13c851f8dc8cfe8d10772269c2_50eed1e5df096d161ffeae7656fa0b75.png)
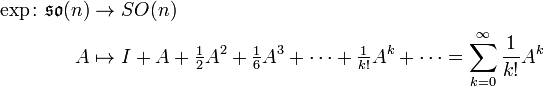
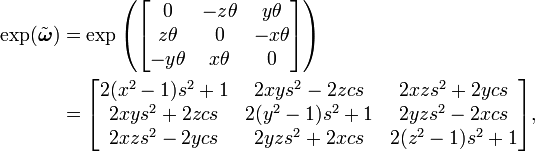
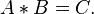
![A \ast B = A + B + \tfrac12 [A,B] + \tfrac{1}{12} [A,[A,B]] - \tfrac{1}{12} [B,[A,B]] - \cdots \,\!](https://static.techno-science.net/illustration/Definitions/autres/2/22d492d59d88b1219aa7a58a065ceccc_a52bc1fca0b00055bd0a20615d82a7c1.png)