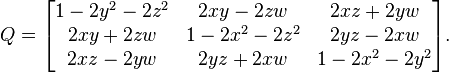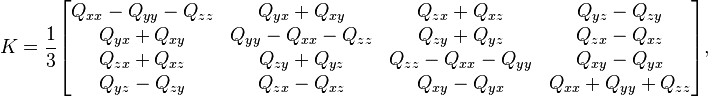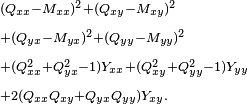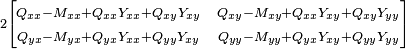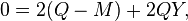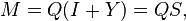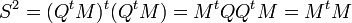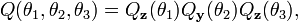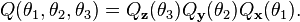Matrice de rotation - Définition
La liste des auteurs de cet article est disponible ici.
Matrices de rotation aléatoires
Il est parfois nécessaire de construire une matrice de rotation aléatoire (avec une distribution uniforme). Intuitivement, il semble clair en dimension 2 que cela implique que l'angle de rotation soit uniformément distribué entre 0 et 2π. Cette intuition est correcte, mais ne s'étend pas aux dimensions supérieures. Ainsi, si nous considérons les matrices de rotation 3×3 sous la forme axe-angle, l'angle ne doit pas être uniformément distribué ; la probabilité que la mesure de l'angle soit au plus θ devrait être1⁄π(θ − sin θ), pour 0 ≤ θ ≤ π.
Comme SO(n) est un groupe de Lie connexe et localement compact, nous avons un critère simple de distribution uniforme, à savoir que la distribution soit invariante par rotation (les "translations" du groupe) ; cette définition correspond à la mesure de Haar. Il est possible d'utiliser la transformation de Cayley pour engendrer et tester des matrice selon ce critère.
On peut également engendrer une distribution uniforme en toute dimension à l'aide de l'algorithme du sous-groupe de Diaconis et Shashani, lequel exploite récursivement la structure des groupes emboîtés de SO(n), de la manière suivante : engendrer un angle au hasard entre 0 et 2π et construire la matrice de rotation 2×2 correspondante. Pour passer de n à n+1, engendrer un vecteur v uniformément distribué sur la n-sphère, Sn, prolonger la n×n matrice en ajoutant comme dernière colonne et dernière ligne (0,…,0,1), et composer par une rotation cette nouvelle matrice pour que la dernière colonne devienne v.
Comme d'habitude, des méthodes plus spécialisées existent pour le cas 3×3. Dans chaque cas, on commence par choisir trois nombres indépendants uniformément distribués entre 0 et 1. Arvo part d'une transformation de Householder et exploite la dimension impaire pour en tirer une rotation en la multipliant par -1, puis pour déterminer l'axe d'une rotation uniformément distribuée.
Une autre méthode part de quaternions de norme 1. La multiplication des matrices est homéomorphe à celle des quaternions, et multiplier par un quaternion unitaire revient à faire tourner la sphère unité. Comme cet homéomorphisme est localement une isométrie, on en conclut qu'on obtiendra une distribution uniforme sur SO(3) en partant d'une distribution uniforme sur S3.
Il est également possible d'utiliser les angles d'Euler, mais avec une distribution non uniforme.
Enfin, sous la forme axe-angle, l'axe doit être uniformément distribué, mais l'angle de rotation a la distribution non-uniforme notée précédemment.
Conversions
Nous avons vu l'existence de plusieurs décompositions et constructions progressives s'appliquant en toutes dimensions. Nous allons à présent nous intéresser de plus près au cas des rotations en dimension 3.
Quaternions
Réécrivons à nouveau la matrice générale de rotation 3×3 sous la forme
À présent, chaque composante d'un quaternion apparaît (doublée) dans un terme de degré 2, et si tous ces termes sont nuls, nous obtenons une matrice identité. Ceci permet une conversion efficace et robuste d'un quaternion quelconque (unitaire ou non, et même nul) vers une matrice de rotation 3×3.
Puisqu'il n'est plus nécessaire que les quaternions utilisés soient unitaires, nous pouvons utiliser les quaternions non nuls comme des coordonnées homogènes pour les matrices de rotation 3×3. La transformation de Cayley discutée plus haut est obtenue en divisant le quaternion par sa composante en w. Pour une rotation de 180° autour d'un axe, w sera nul, ce qui explique la limitation de Cayley.
La somme des termes de la diagonale principale (la trace), vaut 3−4(x2+y2+z2), c'est-à-dire 2w2+2w2-1. On voit que les termes de la diagonale ont tous la même forme : 2x2+2w2−1, 2y2+2w2−1, et 2z2+2w2−1.
La diagonale de la matrice permet ainsi de comparer les valeurs absolues des quatre composantes du quaternion ; nous pouvons en fait les obtenir en n'utilisant que des sommes et des racines carrées, et déterminer les signes à l'aide des coefficients (antisymétriques) hors de la diagonale.
w = 0.5*sqrt(1+Qxx+Qyy+Qzz) x = copysign(0.5*sqrt(1+Qxx-Qyy-Qzz),Qzy-Qyz) y = copysign(0.5*sqrt(1-Qxx+Qyy-Qzz),Qxz-Qzx) z = copysign(0.5*sqrt(1-Qxx-Qyy+Qzz),Qyx-Qxy)
où copysign(x,y) est x avec le signe de y:
- copysign(x,y)
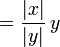
Ou encore, en n'utilisant qu'une racine carrée et une division :
t = Qxx+Qyy+Qzz r = sqrt(1+t) s = 0.5/r w = 0.5*r x = (Qzy-Qyz)*s y = (Qxz-Qzx)*s z = (Qyx-Qxy)*s
Ceci est numériquement stable tant que la trace, t, n'est pas négative, sinon on risque une division par zéro (ou un nombre très petit).
Supposons alors que Qxx soit le plus grand terme de la diagonale, et donc que x ait la plus grande valeur absolue (les autres cas sont analogues) ; alors ce qui suit est sans risque :
r = sqrt(1+Qxx-Qyy-Qzz) s = 0.5/r w = (Qzy-Qyz)*s x = 0.5*r y = (Qxy+Qyx)*s z = (Qzx+Qxz)*s
Si la matrice n'est pas connue exactement (par exemple à la suite d'approximations numériques successives), nous pouvons construire une matrice symétrique 4×4,
et chercher le vecteur propre, (x,y,z,w), correspondant à sa plus grande valeur propre (en valeur absolue) ; si Q est vraiment une matrice de rotation, cette valeur propre vaudra 1. Le quaternion ainsi obtenu correspondra à la matrice de rotation la plus proche de la matrice initiale.
Décomposition polaire
Si M, une matrice n×n, est régulière, ses colonnes forment une base, que le procédé d'orthogonalisation de Schmidt permet de transformer en une base orthonormale. En termes d'algèbre linéaire numérique, nous transformons M en une matrice orthogonale Q, à l'aide de la décomposition QR. Cependant, on préfèrerait souvent obtenir la matrice Q « la plus proche » de M, ce que cette méthode échoue à faire ; l'outil approprié pour cela est la décomposition polaire.
Pour mesurer la proximité des matrices, nous pouvons utiliser n'importe quelle norme invariante par transformations orthogonales. Un choix approprié est celui de la norme de Frobenius, ||Q−M||F, la racine carrée de la somme des carrés des différences des termes de Q et de M. Exprimé en termes de la trace, Tr, notre but est de
- Trouver Q minimisant Tr( (Q−M)t(Q−M) ),sous la contrainte QtQ = I.
Bien qu'écrite en termes matriciels, la fonction d'optimisation est simplement un polynôme quadratique. Nous pouvons le minimiser simplement en cherchant où sa dérivée s'annule. Pour une matrice 3×3, la condition d'orthogonalité entraîne six égalités (scalaires) que doivent satisfaire les coefficients de Q. Pour y ajouter les contraintes, on peut employer la méthode standard des multiplicateurs de Lagrange, formant ici une matrice symétrique Y. Ainsi, notre méthode consiste à :
- Dériver Tr( (Q−M)t(Q−M) + (QtQ−I)Y ) par rapport aux termes de Q, et chercher où ces dérivées partielles s'annulent.
Considérons un exemple 2×2. Avec les contraintes, nous cherchons à minimiser
Prenant successivement les dérivées par rapport à Qxx, Qxy, Qyx et Qyy, nous formons une matrice.
En général, nous obtenons l'équation
et donc
où Q est orthogonale et S est symétrique. Pour assurer un minimum, la matrice Y (et donc aussi S) doit être définie positive. QS s'appelle la décomposition polaire de M, où S est la racine carrée positive de S2 = MtM.
Quand M est inversible, les facteurs Q et S de la décomposition polaire sont uniques. Cependant, le déterminant de S est positif, car S est définie positive, ainsi Q est du signe du déterminant de M. Ainsi, Q est seulement garantie orthogonale, et non une matrice de rotation. Ceci est inévitable ; on ne peut définir (avec unicité) une matrice de rotation la plus proche d'une matrice M de déterminant négatif.
Axe et angle de rotation
Pour construire efficacement une matrice de rotation à partir d'un angle θ et d'un vecteur axial unitaire u, nous pouvons utiliser les symétries (et antisymétries) entre les termes :
c = cos(θ); s = sin(θ); C = 1-c xs = x*s; ys = y*s; zs = z*s xC = x*C; yC = y*C; zC = z*C xyC = x*yC; yzC = y*zC; zxC = z*xC [ x*xC+c xyC-zs zxC+ys ] [ xyC+zs y*yC+c yzC-xs ] [ zxC-ys yzC+xs z*zC+c ]
Déterminer un axe et un angle, comme déterminer un quaternion, n'est possible qu'au signe près ; en effet, (u,θ) et (−u,−θ) correspondent à la même matrice de rotation, tout comme q et −q. Mais cette détermination présente des difficultés supplémentaires : l'angle peut être restreint à l'intervalle entre 0° et 180°, mais les angles ne sont définis qu'à 360° près. De plus, quand l'angle est nul, l'axe n'est pas défini; quand l'angle est 180°, la matrice devient symétrique, ce qui rend difficile la détermination de l'axe. Ainsi, près des multiples de 180°, il faut prêter beaucoup d'attention aux incertitudes numériques : en déterminant l'angle, une fonction arctangente à deux variables (avec atan2(sin θ,cos θ) égal à θ) est nécessaire pour éviter l'insensibilité de arccos ; de même, en calculant la norme d'un vecteur de l'axe (pour construire un vecteur unitaire) une approche en force brute peut perdre trop de précision. On peut souvent utiliser
x = Qzy-Qyz y = Qxz-Qzx z = Qyx-Qxy r = hypot(x,hypot(y,z)) t = Qxx+Qyy+Qzz θ = atan2(r,t−1)
Les composants x, y, et z de l'axe doivent ensuite être divisés par r. Comme pour la représentation par quaternions, des formules différentes doivent être utilisées quand t est négatif ; enfin, quand r est nul (parce que l'angle est nul), un axe doit être fourni arbitrairement.
Angles d'Euler
La complexité de la conversion est plus grande dans le cas des angles d'Euler (ici envisagés dans le sens le plus général). La première difficulté est de déterminer quel ordre d'axes cartésiens utiliser (parmi les 24 possibles). Supposons que les trois angles soient θ1, θ2, θ3 ; les physiciens et les chimistes peuvent les interpréter comme
alors que les aérodynamiciens utiliseront
Une approche systématique commence par choisir l'axe le plus à droite. Parmi toutes les permutations de (x,y,z), deux seulement placent cet axe en premier ; l'une est paire et l'autre impaire. Le choix de la parité permet ainsi de déterminer l'axe du milieu, laissant deux choix pour l'axe le plus à gauche, répétant ou non le premier choix. Ceci donne 3×2×2 = 12 variations ; choisissant des axes fixes ou mobiles, on aboutit à 24 possibilités.
Cela suffit à construire une matrice à partir des angles, mais de nombreux triplets différents peuvent donner la même matrice. Ainsi, si nous utilisons la convention zyz choisie plus haut, nous avons les paires équivalentes suivantes :
-
(90°, 45°, −105°) ≡ (−270°, −315°, 255°) multiples de 360° (72°, 0°, 0°) ≡ (40°, 0°, 32°) alignement singulier (45°, 60°, −30°) ≡ (−135°, −60°, 150°) bascule bistable
Le problème de l'alignement singulier, l'analogue mathématique du phénomène physique de blocage de cardan (gimbal lock) se produit lorsque la rotation intermédiaire aligne les axes des deux autres rotations. Ces singularités ne sont pas caractéristiques de la matrice de rotation elle-même, et ne se produisent que lors de l'utilisation des angles d'Euler.
Pour les éviter, il faut manipuler la matrice en tant que famille de vecteurs-colonnes (ou lignes) orthonormale (appelés souvent, dans les applications 3D, vecteurs "droit", "haut" et "extérieur"); elles ne se produisent également pas lorsqu'on utilise les quaternions.