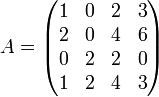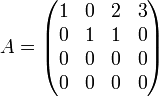Rang (mathématiques) - Définition

Introduction

En algèbre linéaire, le rang d'une famille de vecteurs est la dimension du sous-espace vectoriel engendrée par cette famille. Par exemple, pour une famille de vecteurs linéairement indépendants, son rang est le nombre de vecteurs.

Le rang d'un endomorphisme f de E dans D est la dimension de l'image de f, qui est un sous-espace vectoriel de E. Le rang d'une matrice est le rang de l'application linéaire qu'elle représente ou encore le rang de la famille de ses vecteurs colonnes. En dimension finie, le théorème du rang relie la dimension de E, la dimension du noyau de f et le rang de f.

Rang d'une matrice

Le rang d'une matrice A, noté rg A, est

• le nombre maximal de vecteurs lignes (ou colonnes) linéairement indépendants,
• la dimension du sous-espace vectoriel engendré par les vecteurs lignes (ou colonnes) de A,
• le plus grand des ordres des matrices carrées inversibles extraites de A,
• la taille du plus grand mineur non nul de A,
• la plus petite des tailles des matrices B et C dont le produit est égal à A,

tous ces nombres étant égaux.

On peut déterminer le rang en procédant à une élimination via la méthode de Gauss-Jordan et en examinant la forme échelonnée obtenue de cette manière.

Exemple

Soit la matrice suivante :

On voit que la 2^e ligne est le double de la première ligne. On note également que la 4^e ligne est égale à la somme de la première avec la troisième. Les lignes 1 et 3 sont linéairement indépendantes. Le rang de cette matrice est donc égal à 2. Une autre manière plus directe est de calculer la forme échelonnée réduite de cette matrice. Cette nouvelle matrice a le même rang que la matrice originale, et le rang correspond au nombre de lignes qui sont non nulles. Dans ce cas, nous avons deux lignes qui correspondent à ce critère.

On remarque que le rang d'une matrice donnée est égal au rang de sa transposée. Pour l'exemple, prenons la transposée de la matrice A ci-dessus :

On voit que la 4ème ligne est triple de la première, et que la troisième ligne moins la deuxième est double de la première.

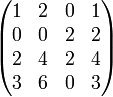
Après échelonnement, on obtient donc :

Et le rang de cette matrice est bien 2.

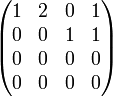
Rang d'une famille de vecteurs

• Pour une famille, son rang correspond au nombre maximal de vecteurs que peut contenir une sous - famille libre de cette famille
• On peut aussi définir le rang d'une famille u par : rg (u) = dim(Vect(u))

Remarque : si est une famille de vecteurs indexée par les entiers de 1 à n, alors le rang de u est le rang de l'application linéaire

.

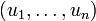
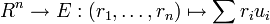
La raison est la suivante : Vect(u) est l'image de cette application linéaire.

Rang d'une application linéaire

Étant donnés deux espaces vectoriels E, F de dimensions finies et une application linéaire f de E dans F, le rang de f est :

• La dimension de l'image de f,
• Le rang de la matrice associée à f dans deux bases de E et F,

ces deux nombres étant égaux. En particulier, le rang de la matrice associée à f ne dépend pas des bases choisies pour représenter f. En effet, la multiplication à droite ou à gauche par une matrice inversible ne modifie pas le rang, ce qui amène rg(P ^{− 1}AQ) = rg(A), où A est la matrice représentant f dans un premier couple de bases, et P,Q des matrices de changement de base.

Propriétés

Soit A une matrice

• Inégalité de Frobenius : rg(AB)+rg(BC) rg(ABC)+rg(B)
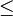
• Théorème du rang : f une application linéaire de E dans F, dim(E)=rg(f)+dim(Ker(f))
• Transposée : rg(A)=rg(A^t)
• Composition : rg(AB) min(rg(A),rg(B))
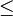
• Addition : rg(A+B) rg(A)+rg(B)
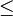
• Le rang d'une famille de vecteurs ne change pas lorsqu'on multiplie un de ses vecteurs par un scalaire non nul, lorsqu'on ajoute à un des vecteurs une combinaison linéaire des autres vecteurs, ou lorsqu'on échange deux vecteurs.
• Deux matrices sont équivalentes si et seulement si elles ont le même rang.

v · d · m Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité
Sous-espace	Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Diagonalisation • Endomorphisme nilpotent
En dimension finie	Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau