Théorème de d'Alembert-Gauss - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématiques, le théorème de d'Alembert-Gauss est parfois appelé le théorème de d'Alembert ou encore le théorème fondamental de l'algèbre. Il indique que tout polynôme non constant, à coefficients dans les nombres complexes, admet au moins une racine. En conséquence, tout polynôme à coefficients entiers, rationnels ou encore réels admet au moins une racine complexe, car ces nombres sont aussi des complexes. Une fois ce résultat établi, il devient simple de montrer que sur
Le temps a rendu l'expression de théorème fondamental de l'algèbre un peu paradoxale. Il n'existe en effet aucune démonstration purement algébrique de ce théorème. Il est nécessaire de faire usage de résultats topologiques ou analytiques pour sa démonstration. L'expression provient d'une époque ou l'algèbre s'identifiait essentiellement avec la théorie des équations, c'est-à-dire la résolution de l'équation polynomiale. Les frontières de l'algèbre ont maintenant changé, le nom du théorème est resté.
Les conséquences du théorème sont nombreuses, en algèbre linéaire ce résultat est essentiel pour la réduction d'endomorphisme, en analyse, il intervient dans la décomposition en éléments simples des fonctions rationnelles utilisée pour trouver une primitive. On les retrouve aussi en théorie de Galois dans un résultat indiquant que tout corps de nombres peut être considéré comme un sous-corps de celui des complexes.
L'histoire du théorème indique l'importance du résultat aux yeux des mathématiciens du XVIIIe siècle. Les plus grands noms, comme ceux de d'Alembert, Euler, Lagrange ou Gauss se sont attelés à sa démonstration, avec des fortunes diverses. La variété et la richesse des méthodes conçues dans ce but fut un moteur puissant pour l'évolution de la recherche en mathématiques et particulièrement pour une meilleure compréhension des nombres complexes.
Énoncés
Le théorème fondamental de l'algèbre admet plusieurs énoncés équivalents.
- Théorème de d'Alembert-Gauss --- Tout polynôme non constant, à coefficients complexes, admet au moins une racine complexe.
Par exemple, 1+i est une racine du polynôme X4 + 4. Sous cette forme, le théorème affirme l'existence d'une racine du polynôme P(X) mais n'explique pas comment trouver explicitement cette racine. Cet énoncé existentiel décrit plus une propriété du corps des nombres complexes. Un corps est dit algébriquement clos si tout polynôme de degré strictement positif et à coefficients dans ce corps admet au moins une racine. Le théorème se reformule donc ainsi :
- Le corps C est algébriquement clos.
Ce résultat se reformule aussi en termes de factorisation des polynômes à coefficients complexes :
- Tout polynôme à coefficients complexes est scindé, c'est-à-dire s'écrit comme un produit de polynômes de degré 1.
Ces résultats indiquent qu'un polynôme à coefficients complexes de degré n, que l'on peut écrire anXn +... + a1X + a0 s'écrit aussi an(X - α1)...(X - αn). Ici, la famille (αk), pour k variant de 1 à n, est celle des racines. Certains nombres αk peuvent être égaux, on parle alors de racines multiples.
Le théorème fondamental de l'algèbre équivaut à chacun des énoncés correspondants pour les polynômes à coefficients réels :
- Tout polynôme non constant à coefficients réels admet au moins une racine complexe.
- Les polynômes irréductibles à coefficients réels sont exactement les polynômes de degré 1, et les polynômes de degré 2 à discriminant strictement négatif (s'écrivant aX2 + bX + c, avec a non nul et b2 − 4ac < 0)
- Tout polynôme non constant à coefficients réels s'écrit comme un produit de polynômes de degrés 1 ou 2.
- Si tout polynôme à coefficients complexes admet une racine, alors tout polynôme à coefficients complexes est scindé.
- Démontrons ce corollaire par récurrence sur n, le degré d'un polynôme. Si n est égal à 1, le résultat est évident. Supposons le résultat établi pour tout polynôme de degré n et soit P un polynôme de degré n + 1. Le théorème fondamental indique l'existence d'une racine α du polynôme P. Le reste de la division du polynôme P par X - α est une constante (la division utilisée est ici euclidienne), ce qui permet d'écrire P sous la forme (X - α)Q + r. Si l'on substitue à l'indéterminée X la valeur α, on obtient 0, ce qui montre que r est nul. Un simple calcul montre que Q est de degré n, il est scindé par hypothèse de récurrence. On a montré que P est le produit d'un polynôme du premier degré et d'un polynôme scindé, la proposition est bien démontrée.
- Réciproque.
- Soit P(X) un polynôme à coefficients complexes. Alors P(X) est scindé, en particulier, il s'écrit sous la forme P(X) = (X − a)R(X) où R(X) est aussi à coefficients complexes. En évaluant en a, il vient : P(a)=0. Donc a est une racine du polynôme P.
- Chacun des énoncés sur les polynômes à coefficients réels implique le théorème de d'Alembert-Gauss.
- Si P(X) est un polynôme à coefficients complexes, on note P * (X) le polynôme obtenu en remplaçant chaque coefficient de P(X) par son conjugué. Alors P(X)P * (X) = R(X).
- Si z est une racine complexe de R(X), alors P(z)P * (z) = 0. Donc, si z n'est pas une racine de P, alors P * (z) = 0 ce qui donne
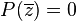
- Si b = a2 + c2, alors
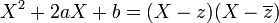
- Si z est une racine complexe de R(X), alors P(z)P * (z) = 0. Donc, si z n'est pas une racine de P, alors P * (z) = 0 ce qui donne
- Un polynôme irréductible à coefficients réels est, soit du premier degré, soit du deuxième degré et de discriminant strictement négatif.
- Soit P un polynôme irréductible à coefficient réel et qui ne soit pas du premier degré. Le théorème fondamental indique l'existence d'une racine complexe α du polynôme P. La valeur α ne peut être réelle, sinon le raisonnement utilisé pour la proposition précédente montrerait que X - α diviserait P, qui ne serait alors pas irréductible. Soit αc le conjugué de α, un rapide calcul montre que αc est aussi racine de P. Les polynômes X - α et X - αc divisent P, ils sont premiers entre eux (cf l'article arithmétique des polynômes), leur produit Q divise aussi P. Un rapide calcul du produit montre que :
-
- le polynôme Q est à coefficients réels, car la somme et le produit de deux complexes conjugués sont réels. La division euclidienne de P par Q donne l'égalité P = Q.M + R, ou M et R sont deux polynômes à coefficients réels et tel que le degré de R est strictement inférieur à celui de Q. Ce résultat peut aussi être lu comme une division euclidienne dans C[X], car le résultat de la division euclidienne est unique. On en déduit que R est un polynôme nul et P est égal à Q.M. Comme P est irréductible, M est une constante, ce qui montre que P est de degré 2.
- Son discriminant est strictement négatif, sinon α serait réel et P ne serait pas irréductible.
![Q = (X - \alpha)(X - \alpha_c) = X^2 - (\alpha + \alpha_c)X + \alpha.\alpha_c \in \mathbb R[X]](https://static.techno-science.net/illustration/Definitions/autres/5/560a10801e1b3af5756be6dda62e1a48_18f1afe220066ec515861961a0a730ef.png)

















































