Théorème de d'Alembert-Gauss - Définition

Usages

Analyse

Il apparaît parfois nécessaire de calculer une primitive d'une fonction rationnelle, c'est-à-dire d'une fonction quotient de deux fonctions polynôme. On peut considérer la fonction f définie par :

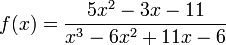
Un corollaire du théorème fondamental indique que le dénominateur se factorise en éléments du premier degré, ici on trouve :

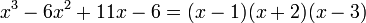
Une décomposition en éléments simples de la fonction montre l'existence de trois valeurs a, b et c telles que :

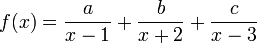
Un rapide calcul montre que a = 3/2, b = 1 et c = 5/2, le calcul de la primitive devient alors aisément réalisable.

Algèbre linéaire

La réduction d'endomorphisme fait appel aux polynômes. On peut choisir comme cas particulier un endomorphisme autoadjoint a d'un espace euclidien E pour illustrer l'usage du théorème. Le polynôme caractéristique de a admet une racine complexe, d'après le théorème fondamental de l'algèbre, c'est une valeur propre λ de b si b est l'endomorphisme de même matrice que celle de a dans une base orthonormale d'un espace hermitien de même dimension que E. La matrice de a est choisie dans une base orthonormale de E. Un rapide calcul montre qu'une valeur propre de b est nécessairement réelle, ce qui montre que a admet une valeur propre, car toute racine réelle du polynôme caractéristique de a est valeur propre. Il suffit de remarquer que l'espace orthogonal F à l'espace propre de valeur propre λ est stable par a pour comprendre que l'endomorphisme est diagonalisable. En effet, il suffit d'appliquer le même raisonnement que le précédent à la restriction de a à F, qui est aussi autoadjointe. En prolongeant ce raisonnement, on finit par diagonaliser a.

Cet exemple est choisi parmi de nombreux autres, la diagonalisation d'un endomorphisme apparait souvent comme la conséquence de l'existence d'une racine du polynôme caractéristique ou minimal.

Arithmétique

Une des méthodes de l'arithmétique consiste à étudier les corps de nombres c'est-à-dire des corps contenant , l'ensemble des nombres rationnels, et qui peuvent être vus comme des -espaces vectoriels de dimension finie. On montre qu'un corps de nombre K est isomorphe à un sous-corps de . Pour s'en rendre compte, le plus simple est de faire usage du théorème de l'élément primitif. Si n est la dimension de K, ce théorème affirme qu'il existe un élément α de K tel que la famille est une base de K, vue comme un -espace vectoriel. Ceci implique que αⁿ est combinaison linéaire de cette base, d'où l'existence de coefficients a_k, tels que :

, aussi noté P(α) = 0 avec

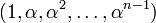
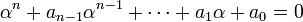
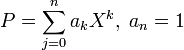
Le polynôme P est irréductible dans Q[X], sinon il existerait un polynôme Q de degré strictement inférieur à P tel que Q(α) soit nul et la famille précédente ne serait pas une base, car Q(α) = 0 serait une combinaison linéaire nulle et non triviale de la famille. Soit β un élément de C racine du polynôme P, qui existe d'après le théorème de d'Alembert. Il suffit alors de vérifier qu'il existe un unique morphisme φ de corps de K dans C qui à α associe β. Comme tout morphisme de corps, il est injectif, ce qui montre que φ est bien un isomorphisme de K dans φ(K), qui est un sous-corps de C.

Éléments d'histoire

Les origines

À l'époque de François Viète , le calcul littéral vient d'être découvert par ce mathématicien ainsi que les relations entre coefficients et racines. Il remarque aussi qu'il est toujours possible de construire une équation ayant exactement n racines données. Au début du XVII^e siècle, Roth prétend que le nombre de racines d'une équation polynomiale est borné par son degré. Par "racine", il n'entendait pas forcément des racines de la forme a+ib. Un premier énoncé correct est donné par Albert Girard , qui, en 1629, dans son traité intitulé Inventions nouvelles en l'algèbre, annonce que :

« Toutes les équations d'algèbre reçoivent autant de solutions que la dénomination de la plus haute quantité le démontre. »

Cette idée est reprise dans la Géométrie de René Descartes , qui utilise pour la première fois le terme imaginaire, pour qualifier des racines : « ... quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine... ». Albert Girard les appelait, pour sa part des inexplicables. Leur compréhension est encore insuffisante pour donner un sens à l'idée d'une démonstration. Un nombre imaginaire est ici un nombre fictif, qui, pour les polynômes de degrés supérieurs, joueraient le même rôle que le symbole √-1 formalisé par Bombelli pour les équations de petit degré.

À cette époque, et pendant plus d'un siècle, ce type de propos n'est pas sujet à démonstration. Prouver une définition, ou encore pire une imagination n'a pas le moindre sens, à cette époque..

L'émergence des nombres complexes

Il faut plus d'un siècle, pour passer des nombres imaginaires, fictifs ou impossibles de Girard et Descartes, aux nombres complexes que nous connaissons, c'est-à-dire de la forme a + i.b, où a et b sont des nombres réels. Petit à petit, les nombres complexes sont apprivoisés par les mathématiciens. À l'aide d'un développement en série, Gottfried Leibniz donne un sens univoque à l'égalité de Bombelli:

L'usage de l'unité imaginaire i devient de plus en plus fréquent, et cela dans des contextes bien différents de celui de la théorie des équations. Le mathématicien Abraham de Moivre démontre la formule qui porte son nom et éclaire la relation entre la trigonométrie et les nombres complexes. Enfin, la célèbre formule d'Euler e^iπ + 1 = 0, publiée en 1748, achève de convaincre les plus sceptiques.

En 1746, Jean le Rond D'Alembert exprime le besoin de démontrer le théorème fondamental de l'algèbre. Sa motivation n'est en rien algébrique, il souhaite démontrer l'existence d'une décomposition en éléments simples de n'importe quelle fonction rationnelle, afin d'en obtenir des primitives. Si le monde mathématique admet immédiatement le bien-fondé de la nécessité d'une démonstration, l'approche de D'Alembert ne séduit pas. Son procédé se fonde sur des convergences de suites et de familles de courbes, une approche purement analytique. Elle est de plus incomplète, et suppose sans preuve qu'une fonction continue sur un compact et à valeurs réelles atteint son minimum. Elle suppose aussi démontré un résultat sur la convergence de séries, maintenant connu sous le nom de théorème de Puiseux. Les grands noms de son époque souhaitent une démonstration algébrique, de même nature que le théorème.

La preuve de D'Alembert fut révisée par Argand en 1814. Ce dernier remplaça le théorème de Puiseux par une simple inégalité, connue aujourd'hui sous le nom d'inégalité d'Argand. Mais la preuve reste incomplète jusqu'au milieu du XIX^e siècle.

Les preuves d'Euler et de Lagrange

Deux tentatives de preuves sont l'œuvre de Leonhard Euler et de Joseph-Louis Lagrange . Elles se suivent et celle plus tardive de Lagrange vise à combler certaines lacunes laissées par Euler.

Les démonstrations n'étudient que le cas où le polynôme est à coefficients réels. On peut remarquer que si le résultat est établi pour les polynômes réels, le passage à un polynôme P à coefficients complexes, n'est guère difficile. Le polynôme P(X).P_c(X), où P_c(X) désigne le polynôme ayant les coefficients conjugués de ceux de P, est à coefficients réels, et si x est une racine du polynôme produit, il l'est aussi du polynôme P.

Ensuite, si le degré n est impair, il est évident que le polynôme admet une racine, car si une grandeur est suffisamment grande, l'image par le polynôme de cette grandeur et de son opposé sont de signes opposés. Il faudra attendre les travaux de Bernard Bolzano de 1816 pour obtenir une démonstration du théorème des valeurs intermédiaires rigoureuse et pour que ce résultat ne soit plus une évidence.

Enfin, Euler et Lagrange considèrent le cas où n est de la forme 2^p.q, où p et q sont des entiers positifs. L'objectif est de montrer par récurrence sur p que toutes les racines imaginaires, au sens de Girard où Descartes, sont complexes au sens où elles sont combinaison linéaire à coefficients réels de 1 et de i. La démonstration d'Euler est rigoureuse pour le degré 4, mais à peine esquissée dans le cas général, celle de Lagrange se fonde sur des fonctions rationnelles invariantes par ce que l'on appelle maintenant un groupe de permutations des racines. D'autres tentatives de même nature sont l'œuvre de Foncenex et de Laplace.

Gauss et la rigueur

Carl Friedrich Gauss écrit sa thèse de doctorat sur le sujet. Il reproche une démarche peu rigoureuse de la part de ses prédécesseurs, à l'exception de d'Alembert qui utilise un raisonnement analytique de nature différente (mais ayant aussi des lacunes). Ils supposent tous l'existence de n racines et montrent que ces racines sont des nombres complexes. Le sens à donner à ces n racines laisse Gauss perplexe, il s'exprime ainsi : « L'hypothèse de base de la démonstration, l'axiome est que toute équation possède effectivement n racines possibles ou impossibles. Si l'on entend par possibles réels et par impossibles, complexes, cet axiome est inadmissible puisque c'est justement ce qu'il s'agit de démontrer. Mais si l'on entend par possibles les quantités réelles et complexes et par impossibles tout ce qui manque pour qu'on ait exactement n racines, cet axiome est acceptable. Impossible signifie alors quantité qui n'existe pas dans tout le domaine des grandeurs. » La faiblesse, c'est que, si elles n'existent pas, et cela dans tout le domaine des grandeurs, est-il raisonnable de calculer dessus comme le font Euler et Lagrange ?

La première preuve de Gauss, présentée en 1799 et fondée sur le canevas de d'Alembert, reste encore incomplète. À l'époque, l'existence d'un minimum atteint par une fonction continue définie sur un compact n'est pas démontrée. En 1814, un amateur suisse du nom de Jean-Robert Argand présente une preuve à la fois solide et simple, fondée sur le canevas de d'Alembert. Cette preuve est reprise par Cauchy, qui en fait un chapitre entier de son cours d'analyse pour l'école Polytechnique. Comme à son habitude, il n'éprouve pas le besoin de citer Argand, le véritable auteur.

Selon Remmert, cette première preuve de Gauss est une belle preuve géométrique, mais reste encore incomplète. Les zéros sont interprétés comme les intersections des deux courbes algébriques réelles ReP = 0 et ImP = 0. En l'infini, ces courbes ont 2n branches qui s'alternent (partie facile de la preuve). Malheureusement, en déduire l'existence de n points d'intersections comptées avec multiplicité n'est pas une application directe du théorème des valeurs intermédiaires. Elle sera seulement donnée par Ostrowski en 1920.

La deuxième preuve de Gauss, fait appel à la démarche d'Euler et de Lagrange. Cette fois-ci, il remplace les racines par des indéterminées, ce qui aboutit à une preuve rigoureuse, mais plus tardive que celle d'Argand.

La troisième preuve de Gauss date de 1816. Il s'agit en réalité d'un résultat sur la localisation des zéros des fonctions polynomiales. Aujourd'hui, ce résultat est étendu aux fonctions dites holomorphes (dont les fonctions polynomiales sont des exemples). Il est connu sous le nom de le théorème de Rouché.

La quatrième preuve de Gauss date de 1849.

La théorie de Galois

L'histoire finit par combler la lacune de la démonstration de Lagrange. Evariste Galois réutilise les idées de Lagrange sous un angle plus novateur et qui préfigure l'algèbre moderne. Ces idées, reprises par Ernst Kummer et Leopold Kronecker, débouchent sur l'existence d'un corps contenant toutes les racines du polynôme, et cela indépendamment de toute construction sur les nombres complexes. Ce corps est appelé corps de décomposition, son usage permet la reprise des idées de Lagrange, de manière tout à fait rigoureuse. La démonstration devient proche de celle de Frobenius, présentée dans cet article dans un langage plus moderne et plus puissant, elle permet aussi de démontrer qu'il n'existe aucun corps commutatif contenant strictement et autre que .

Remmertattribue cette réactualisation de la preuve de Lagrange à Adolf Knesser.

Démonstrations itératives et effectivité

Même complétée et corrigée, la démonstration de D'Alembert et d'Argand n'est pas constructive : elle utilise que le module d'un polynôme atteint son minimum, sans préciser en quel point. Il serait pourtant souhaitable de pouvoir approcher les racines des polynômes, par exemple en disposant d'une démonstration qui explicite une manière d'exhiber une racine, ou une suite de nombres nombre complexes qui converge vers une racine. Des théorèmes de localisation sur les zéros des fonctions holomorphes peuvent être déduits du théorème des résidus dû à Cauchy, mais ne sont pas réellement effectifs : il est par exemple impossible d'implémenter un algorithme d'approximation fondé sur ceux-ci.

Selon Remmert, la première tentative significative fut proposée par Weierstrass en 1859. Bien que la méthode proposée ne fonctionne pas bien, l'idée est intéressante : il s'agit d'itérer la fonction . Ceci donne lieu à une suite qui, si elle converge, converge vers un zéro de P. Cette idée est exploitée pour montrer le théorème du point fixe pour les fonctions contractantes par exemple. Cependant, la convergence n'est, ici, pas automatique : les valeurs de x pour lesquelles la suite itérée est bornée n'est pas C en général et forme une des "fractales" les plus connues : les ensembles de Julia dont la dimension de Hausdorff peut être non-entière. Cette dimension peut en particulier être non-nulle, ce qui signifie que cet ensemble peut être "assez gros" en un certain sens.

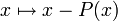
Si les racines du polynôme P étudié sont simples (ce qui est une condition générique), la méthode de Newton peut être appliquée. Elle consiste à itérer la fonction , qui à x associe le point d'annulation de la tangente de P en x. Encore une fois, si cette suite converge, sa limite est un zéro de P et la convergence est assurée si la valeur initiale est choisie suffisamment proche d'une racine de P.

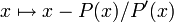
Une importante correction a été apportée par Stephen Smale en 1979. Elle consiste à itérer la fonction

où la fonction H est définie en fonction du polynôme P par la formule .

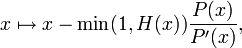
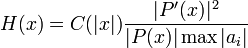
Les a_i sont les coefficients de P, et C est une fonction rationnelle d'une variable réelle. Smale démontra que la suite obtenue z_n converge toujours vers un zéro du polynôme P, quelle que soit la valeur initiale z₀.