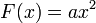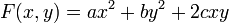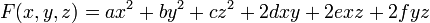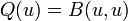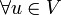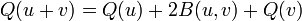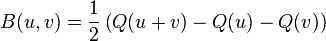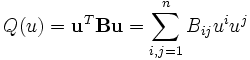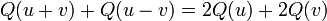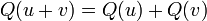Forme quadratique - Définition
En mathématiques, une forme quadratique est un polynôme homogène de degré deux avec un nombre quelconque de variables. Par exemple, la distance comprise entre deux points dans un espace euclidien à trois dimensions s'obtient en calculant la racine carrée d'une forme quadratique impliquant six variables qui sont les trois coordonnées de chacun des deux points.
Les formes quadratique d'une, deux et trois variables sont données par les formules suivantes :
Forme quadratique sur un espace vectoriel
Soit un espace vectoriel V sur un corps F. Pour l'instant, nous supposons que F possède une caractéristique différente de 2. C'est le cas, en particulier, pour les corps réels et complexes qui sont de caractéristique 0. Le cas où la caractéristique vaut 2 sera traité séparément.
Une application Q :
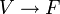
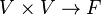
B est appelée la forme bilinéaire associée. Notons que pour tout vecteur
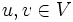
donc nous pouvons retrouver la forme bilinéaire B à partir de Q :
C'est un exemple de polarisation d'une forme algébrique. Il existe alors une correspondance bijective entre les formes quadratiques sur V et les formes bilinéaires symétriques sur V. À partir d'une forme donnée, nous pouvons définir de manière unique l'autre forme.
Si V est de dimension n, nous pouvons écrire la forme bilinéaire B comme une matrice symétrique B relative à une certaine base
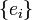
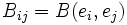
où
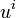
Quelques autres propriétés des formes quadratiques :
-
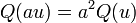
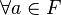
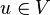
- Q obéit à la loi du parallélogramme :
- Les vecteurs u et v sont orthogonaux par rapport à B ssi
Cas de corps de caractéristique deux
La théorie des formes quadratiques de caractéristique deux possède une petite saveur différente, essentiellement parce que la division par 2 n'est pas possible. Il n'est plus vrai non plus que chaque forme quadratique est de la forme Q(u) = B(u,u) pour une forme bilinéaire symétrique B. En outre, même si B existe, elle n'est pas unique : puisque les formes alternées sont aussi symétriques en caractéristique deux, on peut ajouter toute forme alternée à B et obtenir la même forme quadratique.
Une définition plus générale d'une forme quadratique qui marche pour toute caractéristique est la suivante. Une forme quadratique d'un espace vectoriel V sur un corps F est comme une application
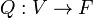
-
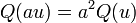
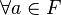
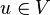
-
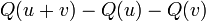
Généralisations
On peut généraliser la notion de forme quadratique à des modules sur un anneau commutatif. Les formes quadratiques entières sont importantes en théorie des nombres et topologie.
| Articles de mathématiques en rapport avec l'algèbre bilinéaire |
| Espace euclidien | Forme bilinéaire | Forme quadratique | Forme sesquilinéaire | Orthogonalité | Base orthonormale | Projection orthogonale | Inégalité de Cauchy-Schwarz | Inégalité de Minkowski | Matrice définie positive | Matrice semi-définie positive | Décomposition QR | Déterminant de Gram | Hermitien | Espace de Hilbert | Base de Hilbert | Théorème spectral | Théorème de Stampacchia | Théorème de Riesz | Théorème de Lax-Milgram | Théorème de représentation de Riesz |