Problèmes de Hilbert - Définition
Lors du deuxième congrès international de mathématiques tenu à Paris en 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu'alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer le cours des mathématiques du XXe siècle, et l'on peut dire aujourd'hui que cela a été grandement le cas. La liste définitive fut publiée après la tenue du congrès et est aujourd'hui familièrement appelée problèmes de Hilbert.
Les sections suivantes présentent brièvement chaque problème.
L'équivalent pour le XXIe siècle a été défini sous le programme des problèmes du prix du millénaire.
Premier problème
Prouver l'hypothèse du continu de Cantor.
Paul Cohen, en se basant sur les travaux de Gödel, montra en 1963 que cette conjecture était indécidable.
Hilbert rattache ce problème à la question suivante : prouver que l'ensemble des nombres réels peut être bien ordonné. Ernst Zermelo prouva que l'existence de ce bon ordre est équivalent à l'axiome du choix de Zermelo. Ainsi, le prouver revient à accepter cet axiome, ce que nombre de mathématiciens refusèrent. Alors que Hilbert pensait que ces deux problèmes étaient liés, Cohen prouva qu'ils étaient indépendants en montrant que l'hypothèse du continu de Cantor était indécidable.
Deuxième problème
Démontrer la consistance des axiomes de l'arithmétique.
Gödel montra en 1931, via son théorème d'incomplétude, que cela ne pouvait être démontré sans sortir de l'arithmétique. Gerhard Gentzen, cependant, donna, en 1936, une réponse affirmative au moyen d'une récurrence transfinie.
Troisième problème
Étant donnés deux polyèdres d'égal volume, peut-on découper le premier polyèdre en des polyèdres et les rassembler pour former le second polyèdre ?
Max Dehn, élève de Hilbert, montra que non, en 1902, en démontrant qu'il était impossible de diviser un cube et un tétraèdre régulier de même volume en un nombre fini de polyèdres deux à deux identiques. Malgré tout, le paradoxe de Banach-Tarski constitue un résultat positif pour cette question si l'on n'exige pas que les morceaux intermédiaires soient des polyèdres et surtout si l'on suppose l'axiome du choix.
Quatrième problème
Définir toutes les géométries dont la plus courte distance entre deux points est un segment de droite.
La géométrie différentielle a permis de répondre en partie à ce problème, bien que l'on ne puisse pas à proprement parler de réponse ferme.
Cinquième problème
Démontrer que les groupes de Lie sont nécessairement différentiables.
Le théorème de Gleason-Montgomery-Zippin en 1953 y répondit par l'affirmative.
Sixième problème
L'axiomatisation, basée sur le modèle mathématique, de la physique.
Du fait de l'apparition de la théorie de la relativité et de la mécanique quantique, le problème fut vite obsolète. Malgré tout, on peut noter que la physique théorique et les mathématiques ne cessent de se rapprocher. En axiomatisant la Théorie des probabilités, Kolmogorov a résolu en partie ce problème.
Septième problème
Démontrer la transcendance des nombres ab, avec a algébrique et b irrationnel (par exemple
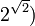
Les travaux de Gelfond, complétés par Schneider et Baker, ont permis de résoudre en partie ce problème (voir Théorème de Gelfond-Schneider).
Huitième problème
Démontrer l'hypothèse de Riemann.
Malgré les progrès faits notamment par Deligne qui démontra les conjectures de Weil, et reçut pour cela la médaille Fields en 1978, on est encore loin d'avoir résolu ce problème, qui s'annonce comme celui du XXIe siècle.
Neuvième problème
Établir une loi de réciprocité dans les corps de nombres algébriques.
Une réponse à ce problème est apportée par la loi de réciprocité d'Artin, démontrée par celui-ci en 1927.Ce théorème enrichit la connaissance de la théorie des corps de classes, dont le développement fut facilité par l'introduction des idèles par Chevalley en 1936.
Dixième problème
Trouver un algorithme déterminant si une équation diophantienne a des solutions.
Il fallut attendre les travaux de Church et Turing en 1930 pour définir rigoureusement la notion d'algorithme. En 1970, Yuri Matijasevic, établissant une équivalence entre les ensembles récursivement énumérables et les ensembles diophantiens, a établi qu'un tel algorithme ne pouvait pas exister.
Onzième problème
Classifier les formes quadratiques à coefficients dans les anneaux d'entiers algébriques.
Le théorème de Hasse-Minkowski résout le problème sur
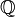
Douzième problème
Prolonger le théorème de Kronecker sur les corps non-abéliens.
Treizième problème
Montrer l'impossibilité de résoudre les équations du septième degré au moyen de fonctions de seulement deux variables.
Plus généralement, il s'agit d'étudier les fonctions continues (et, en fait, les fonctions continues de trois variables) qui ne peuvent pas s'exprimer par composition à partir de fonctions continues de deux variables. En 1954, Kolmogorov et son élève Vladimir Arnold ont montré que cette classe était vide : il existe n(2n + 1) fonctions continues universelles Φij (de [0;1] dans [0;1]) telles que pour toute fonction continue
![f:[0;1]^n \to [0;1]](https://static.techno-science.net/illustration/Definitions/autres/f/ff49e287250297e479a4deb2e62a514e_6a468978aa9b36b0c3fbb118ad225c68.png)
![g_j :[0;1] \to [0;1]](https://static.techno-science.net/illustration/Definitions/autres/8/88b87551bcd4949ecd397a3943c35a15_a7e25cc5dddb5da8426ad25c290f4e47.png)
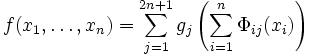
Quatorzième problème
Prouver le caractère fini de certains systèmes complets des fonctions.
Le problème est le suivant : on considère un corps k et un sous-corps K de
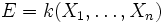
![R = k[X_1 , \dots, X_n ]](https://static.techno-science.net/illustration/Definitions/autres/7/7e3151a34a4bb6278e53303fb36457d6_5f9c0b08eb098520cc145fb1ba327ec9.png)
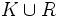
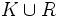
Nagata donna en 1959 un contre-exemple qui montra la fausseté de la conjecture.
Quinzième problème
Mettre en place les bases du calcul énumératif de Hermann Schubert.
Il s'agit là de rendre rigoureux certains calculs sur les objets " en position générale " en théorie de l'intersection, et en particulier le " principe de conservation des nombres ". Ce problème a donné naissance aux théories de la multiplicité de Samuel et Grothendieck.
Résolu par Van der Waerden en 1930.
Seizième problème
Développer une topologie des courbes et des surfaces algébriques.
Ce problème comporte deux parties. La première concerne le nombre de branches réelles d'une courbe algébrique, et leur disposition ; de nombreux résultats modernes (Petrovskii, Thom, Arnold) apportent des informations à leur sujet. La seconde partie du problème pose la question de l'existence d'un nombre maximal de cycles limite pour une équation différentielle linéaire définie par des polynômes homogènes de degré donné ; cette question est encore ouverte.
Dix-septième problème
Montrer qu'une fonction rationnelle positive peut s'écrire sous la forme de somme de carrés de fonctions rationnelles.
Résolu par Artin en 1927. Une démonstration purement logique a été trouvée par Robinson.
Dix-huitième problème
Construire un espace euclidien avec des polyèdres congruents.
Le problème comporte trois parties.
- Premièrement, montrer qu'il n'existe à isomorphisme près qu'un nombre fini de groupes discrets d'isométries de
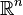
- Deuxièmement, la question de l'existence de polyèdres qui ne sont pas des groupes fondamentaux, mais qui peuvent cependant paver l'espace ; de tels polyèdres furent construits par Reinhardt et Heesch dans les années trente.
- Troisièmement, ce problème comporte aussi la fameuse conjecture de Kepler sur l'empilement des sphères dans l'espace, résolue en 1998 par Thomas Hall.
Dix-neuvième problème
Prouver que le calcul des variations est toujours nécessairement analytique.
Résolu par Bernstein et Tibor Rado en 1929.
Vingtième problème
Étudier la solution générale des problèmes de valeur limite.
Vingt-et-unième problème
Prouver que toute représentation complexe de dimension finie peut s'obtenir par action de monodromie sur une équation différentielle de Fuchs.
Résolu par Helmut Rörl en 1957.
Vingt-deuxième problème
Uniformiser des courbes analytiques au moyen de fonctions automorphes.
Résolu par Koebe et Henri Poincaré en 1907.
Vingt-troisième problème
Développer une méthode générale de résolution dans le calcul des variations.

















































