Boson - Définition

Photons émis dans le faisceau cohérent d'un laser.

Articles de physique quantique

Théorie quantique

Électrodynamique quantique

Mécanique quantique

Théorie des champs

Modèle standard

Statistiques quantique

Bose-Einstein

Fermi-Dirac

Maxwell-Boltzmann

Physiciens

Bohr - de Broglie

Bose - Einstein

Fermi - Dirac

Heisenberg - Pauli

Schrödinger - Feynman

Les bosons représentent une classe de particules qui possèdent des propriétés de symétrie particulières lors de l'échange de particules : un système de particules identiques se comportant comme des bosons est toujours dans un état totalement symétrique vis à vis de l'échange de particules. Toutes les particules élémentaires découvertes à ce jour sont soit des bosons, soit des fermions, ces derniers ne pouvant être que dans un état totalement antisymétrique vis à vis de l'échange de particules. Le théorème spin-statistique indique que les particules de spin entier sont des bosons, alors que les particules de spin demi-entier sont des fermions.

Historique

Le terme de boson provient du nom du physicien Satyendranath Bose et aurait été utilisé pour la première fois par Paul Dirac^[1]. Bose réalisa le premier que pour expliquer la loi de Planck décrivant le rayonnement du corps noir à partir des photons précédemment découverts par Einstein, il fallait supposer que les photons ne suivent pas la statistique de Maxwell-Boltzmann, mais plutôt une statistique désormais appelée statistique de Bose-Einstein. Bose écrit un court article, Planck's Law and the Hypothesis of Light Quanta, qu'il envoie à Albert Einstein, après un rejet par le Philosophical Magazine. Einstein est favorablement impressionné et le recommande pour publication dans Zeitschrift für Physik, et il en fait lui-même la traduction de l'anglais vers l'allemand. Einstein va également étendre la notion de boson à d'autres particules telles que les atomes et contribuer à la popularité du concept de boson.

Échange de particules identiques en mécanique quantique

Le fait qu'en mécanique quantique les particules ne suivent pas une trajectoire déterminée rend l'identification des particules complètement impossible. Autrement dit, les particules sont indistinguables l'une de l'autre, et n'ont pas d'individualité propre. Il s'en suit qu'une mesure complète sur chacune des particules ne peut suffire à caractériser complètement l'état du système, ce phénomène étant dénommé dégénérescence d'échange.

Pour illustrer ce que l'on entend par dégénérescence d'échange, supposons donné un ensemble complet d'observables qui commutent (ECOC) pour une particule et notons la base de vecteurs propres communs à toutes les observables de cet ECOC. Si le système est composé d'une seule particule, et que l'on mesure toutes les observables de l'ECOC, d'après les postulats de la mécanique quantique, on va projeter l'état du système sur l'un des vecteur | u_p > , de sorte que l'état du système après la mesure sera complètement connu. Supposons maintenant que le système soit composé de deux particules et que l'on effectue une mesure complète de chacune des particules. Le résultat que l'on obtient sera : une particule est dans l'état | u_p > et l'autre est dans l'état | u_p' > , mais puisqu'on ne peut pas identifier les particules, on ne sait pas laquelle est dans | u_p > et laquelle est dans | u_p' > . En conséquence, le vecteur mathématique décrivant l'état du système est indéterminé. Ce peut être :

1. ,
2. , en échangeant le rôle des particules par rapport à ci-dessus,
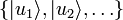
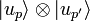
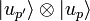
3. ou n'importe quel vecteur de l'espace engendré par ces deux vecteurs.

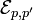
Pour lever la dégénérescence d'échange, on construit deux opérateurs S et A qui projettent l'espace sur un ket unique soit complètement symétrique lors de l'échange de deux particules (dans le cas de S), soit complètement antisymétrique (dans le cas de A). On postule ensuite que le vecteur représentant correctement l'état du système est ce ket unique. Les particules ayant un vecteur d'état complètement symétrique sont les bosons, tandis que celles ayant un vecteur d'état complètement antisymétrique sont les fermions. Notons que des travaux récents de physique théorique ont découverts d'autres moyens de résoudre ce problème qui conduisent à des comportements différents, tels que les anyons ou les plektons en théorie des cordes. Toutefois, toutes les particules élémentaires décrites par le modèle standard sont soit des bosons lorsque leur spin est entier, soit des fermions lorsque leur spin est demi-entier.

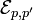
Particules élémentaires se comportant comme des bosons

Parmi les particules élémentaires découvertes à ce jour, les bosons sont tous des bosons de jauge, c’est-à-dire qu'ils agissent comme des intermédiaires des interactions fondamentales :

• le photon est le vecteur de l'interaction électromagnétique
• les huit gluons de l'interaction forte
• les bosons Z⁰, W^- et W⁺ de l'interaction faible

Le modèle standard de la physique des particules prédit l'existence de deux particules supplémentaires, le boson de Higgs, objet de nombreuses recherches, mais qui n'a pas été mis en évidence jusqu'à présent, et le graviton, boson de jauge qui serait responsable de l'interaction gravitationnelle.

En étudiant les propriétés de biréfringence du vide, l'équipe italienne PVLAS a montré l'existence possible d'un boson très léger, l'axion^[2], de masse 1-1.5 meV. L'effet observé peut cependant être expliqué différemment (lien), et d'autres expériences sont en cours pour confirmer ou infirmer l'existence de cette particule.

Bosons composites

Les particules composées de particules plus élémentaires, comme par exemple les atomes ou le proton, peuvent être des fermions ou des bosons, selon leur spin total (entier pour les bosons, demi-entier pour les fermions).

Exemples de bosons composites :

• atome d'hélium 4
• état de deux électrons formant une paire de Cooper dans les matériaux supraconducteurs
• exciton
• polariton

Phénomènes montrant le comportement bosonique

Alors que les fermions obéissent au principe d'exclusion de Pauli : " Un état quantique donné ne peut être occupé que par au plus un seul fermion ", ce n'est pas le cas des bosons. Un état quantique bosonique peut être occupé par un nombre quelconque de bosons. C'est même l'inverse qui se produit et les bosons tendent à se rassembler dans un état quantique donné.

En conséquence, comme de nombreux noyaux ou atomes sont des bosons, dans certains cas ils peuvent s'accumuler dans le même niveau. Ceci permet d'expliquer :

• le rayonnement du corps noir, qui s'explique par la statistique des photons ;
• la population macroscopique d'un mode unique de photon dans un laser ;
• l'effondrement des atomes dans l'état de plus basse énergie à basse température (condensation de Bose-Einstein), qui est à la base des propriétés superfluides de l'Hélium 4 liquide à basse température ;
• le groupement des photons lors de leur détection (expérience de Hanbury-Brown et Twiss)

Notes et références de l'article

• Chapitre XIV sur les particules identiques du livre de Claude Cohen-Tannoudji, Bernard Diu et Frank Laloë, Mécanique quantique vol. I et II, Collection Enseignement des sciences, Paris (1973) ISBN 2-7056-5733-9
• S.N. Bose. "Plancks Gesetz und Lichtquantenhypothese", Zeitschrift für Physik 26:178-181 (1924). (La traduction en Allemand de l'article de Bose sur la loi de Planck)
• Version anglaise de l'article précédent