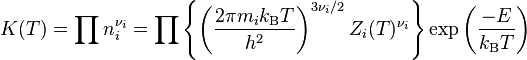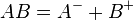Constante d'équilibre - Définition

Introduction

En chimie, une constante d'équilibre caractérise l'état d'équilibre d'une réaction. Elle représente donc un état qui ne peut pas évoluer de manière spontanée. La valeur de la constante d'équilibre dépend uniquement de la réaction chimique considérée et de la température. Les constantes d'équilibre sont généralement données à 25 °C.

Claude-Louis Berthollet fut le premier, en 1803, à comprendre que toutes les réactions chimiques ne sont pas totales. Dans son Essai de statique chimique, il écrivit la première formule permettant de définir a priori les quantités présentes à l'équilibre. C'est en observant les bords d'un « lac de natron » lors d'une expédition en Égypte avec Napoléon Bonaparte et Gaspard Monge qu'il arriva à cette conclusion, originale pour l'époque. Les bords du lac salé étaient couverts de carbonate de sodium. Il établit que les deux réactifs (du chlorure de sodium - du sel - et du carbonate de calcium) réagissent aussi avec les produits de réaction.

Définition

En considérant l'équation chimique suivante :

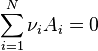
où

• A_i est une espèce chimique,
• ν_i est le coefficient stoechiométrique de l'espèce A_i (ν est positif pour les produits de la réaction et négatif pour les réactifs),
• N le nombre de constituants.

La constante d'équilibre est définie par la relation :

où

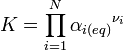
• α_i(eq) est l'activité chimique de l'espèce i à l'équilibre,
• est l'opérateur produit.

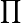
La constante d'équilibre K est une grandeur sans unité.

Notion d'activité

L'activité chimique d'une espèce est l'influence de la quantité d'une espèce sur l'énergie libre du système. Elle se définit schématiquement comme la « concentration active » de l'espèce en solution. Elle est :

• égale à 1 si l'espèce est un solvant, ou plus généralement une phase pure,
• égale à la concentration molaire de l'espèce sur la concentration de référence C⁰ que l'on choisit égale à 1 mol.L^-1 si l'espèce est un soluté,
• égale au rapport de la pression partielle (en bar) de l'espèce rapportée à une pression de référence p⁰ que l'on choisit égale à 1 bar si l'espèce est un gaz.

Lien avec l'enthalpie libre

L'enthalpie libre standard : d'une réaction chimique effectuée à température (T) et pression (P) constantes, est reliée à la constante d'équilibre par la relation :

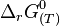
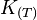
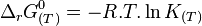
où R est la constante des gaz parfaits et T est la température absolue (en kelvin).

D'où

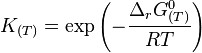
La constante d'équilibre est donc une grandeur thermodynamique (elle caractérise l'équilibre du système), et n'a pas d'incidence sur la cinétique (vitesse de réaction) de ce système.

En physique statistique

Pour la réaction

,

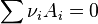
en notant ν_i < 0 pour désigner les produits, la constante d'équilibre s'écrit

où

• m_i désigne la masse du réactif ou produit A_i ;
• Z_i(T) est la fonction de partition interne de l'espèce A_i ;
• E est l'énergie consommée requise par la réaction (E < 0 pour une réaction exothermique) ;
• T est la température ;
• k_B est la constante de Boltzmann ;
• h est la constante de Planck.

Constantes d'équilibre particulières

Équilibres acido-basiques : K_A, K_B

• Lors de la dissolution d'un acide dans l'eau entre en jeu une réaction acide-base du type : (avec AH un acide et A^- sa base conjuguée)

AH + H₂O = A^- + H₃O⁺

On définit alors comme constante d'acidité :

où C⁰ vaut 1 mol l^-1. K_A est par conséquent sans unité.

Plus la constante d'acidité est grande, plus l'acide se dissocie dans l'eau, et donc plus l'acide est fort.

Par commodité, on utilise souvent le pK_a au lieu du K_a, défini ainsi : pK_A = − log₁₀K_A; le pK_a est souvent tabulé à 25 °C.

• Par analogie, on définit aussi la constante de basicité K_B. (Soit B la base et BH⁺ l'acide conjugué)

B + H₂O = BH⁺ + HO^- ;

On a alors : et de même pK_B = − log₁₀K_B

États de réactions entre deux couple acide/base : K_A1, K_A2

Lors de la réaction dans l'eau d'un acide(AH₁) et d'une base(A₂^-) il est possible de déterminer à partir de la constante d'acidité l'état de la réaction : Très peu avancé, équilibre ([A₁^-]=[A₂^-]), totale.

Formule générale

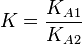
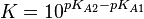
Utilisation

• Si K < 10^-4, alors la réaction est très peu avancée.
• Si 10^-4 < K < 10⁴, alors il y a un état d'équilibre.
• Si 10⁴ < K, alors la réaction est totale.

Solubilité des sels, le produit de solubilité K_s

Le K_s mesure la solubilisation des sels dans un solvant donné. Si dans le solvant donné, le sel AB se décompose selon l'équation

alors le produit de solubilité K_s est défini par :

(valeurs à saturation, c'est-à-dire à l'équilibre entre sel précipité et sel dissous).

Plus K_s est grand, plus le sel étudié est soluble dans le solvant.