Effet Yarkovsky - Définition

Introduction

L'effet Yarkovsky se manifeste par une force de radiation thermique qui change le demi-grand axe a d'un astéroïde en fonction de son moment cinétique, de son orbite et de quelques propriétés de ses matériaux. Il peut aussi changer un peu la rotation de celui-ci, mais comparé à l'effet YORP, il est négligeable.

Il agit sur des astéroïdes dont le diamètre D est inférieur à environ 20 km, et peut mettre ceux appartenant à la ceinture principale en résonance, et donc sur des orbites géocroiseurs [Bottke Jr. et al., 2002].

Notations

Seront utilisées par la suite les notations suivantes pour l'astéroïde :

• R : rayon moyen ;
• D : diamètre moyen ;
• E : obliquité de l'axe de rotation ;
• ω : période de rotation ;
• P : période de rotation ;
• κ : conductivité thermique ;
• ρ :densité volumique ;
• C : chaleur spécifique à pression constante ;
• T : température de surface ;
• A : albédo de Bond ;
• m : masse ;
• S : surface ;
• ε : émissivité thermique de la surface ;

ainsi que les constantes physiques suivantes :

• c : vitesse de la lumière ;
• σ : constante de Stefan-Boltzmann.

Brève théorie

Il y a deux étapes dans le calcul de la force Yarkovsky [Bottke Jr. et al., 2002] :

1. détermination de la distribution de température à la surface,
2. évaluation de la force de recul due à la radiation thermique.

Température de surface

Pour déterminer la distribution de température à la surface de l'astéroïde, on doit prendre en compte l'inertie thermique de celui-ci, la vitesse de rotation, et la diffusion de chaleur. Cette dernière est trop complexe pour pouvoir la traiter analytiquement sans simplification. On la linéarise donc, ce qui revient à considérer des petites variations de chaleur [Vokrouhlicky, 1999].

Fig. 3 - L'effet Yarkovsky diurne. Un photon incident frappe la surface de l'astéroïde (en rouge), puis est réémis après un certain temps τ (caractéristique de l'inertie thermique) perpendiculairement à la surface (voir pression de radiation) de l'astéroïde (en vert). En moyenne (sur la surface ensoleillé) la force sera donc orientée d'un angle dα(τ) par rapport à la direction d'incidence des photons (en magenta).

Pour des astéroïdes de forme complexe et/ou de paramètres thermiques hétérogènes, le calcul nécessite un traitement plus sophistiqué pour éviter des calculs trop gourmands en temps. Ainsi, on déterminera la température de surface en utilisant le flux d'énergie à l'intérieur de l'astéroïde :

,

et la condition limite à la surface de l'astéroïde :

.

La dernière équation se réfère à un élément de surface orientée par le vecteur unitaire  ; E est le flux solaire à travers cette surface, et . Cette équation est une condition limite pour la détermination de la température T mais requiert la connaissance de la forme et l'état de rotation de l'astéroïde par le biais de E, ce qui implique de longs temps de calcul.

Dans le cas de petites variations thermiques, on peut dire que la température T autour du corps est proche de T (c'est-à-dire T = T₀ + ΔT, la variation de temprétature étant petite devant T : ). Si T est constant, ces deux équations peuvent être réécrites pour la variable δ, tandis qu'on peut écrire le terme de température de la dernière équation comme suit [Vokrouhlicky, 1998] :

.

Évaluation de la force

L'astéroïde conserve presque toujours une asymétrie dans son irradiation (à l'exception des très petits corps de moins de 10 centimètres de diamètre, qui sont gardés isothermes par une conduction de chaleur interne efficace). Il en résulte donc une direction privilégiée vers laquelle la force va agir [Vokrouhlicky et al., 2005].

À ce stade, il parait utile de mettre en évidence quelques grandeurs caractéristiques. Pour un terme de Fourier donné à la fréquence ν de la décomposition de E, deux paramètres fondamentaux apparaissent [Vokrouhlicky et al., 2000 ; Bottke Jr. et al., 2002] :

• la profondeur de pénétration de l'onde thermique dans l'astéroïde : ,
• le paramètre thermique , qui permet de mesurer la relaxation entre l'absorption et la réémission à la fréquence ν d'un photon, T étant la température subsolaire définie comme , où est le flux de radiation solaire à la distance de l'astéroïde.

Pour les astéroïdes qui viennent de la ceinture principale, on pourra considérer une excentricité e petite, ce qui permet de linéariser le terme δ. Enfin, on supposera une émission isotropique des photons, ce qui correspond à l'approximation de Lambert.

Avec toutes les simplifications précédentes, on obtient l'expression de la force due à l'effet Yarkovsky suivante :

,

où f est la force par unité de masse, et (u, v) les coordonnées de l'élément de surface.

Si on adopte un système local de coordonnées avec z selon l'axe de rotation de l'astéroïde et x, y dans le plan équatorial, on différencie alors deux variantes de  :

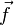
• l'effet diurne : f, f dépendent de la fréquence de rotation ω
• l'effet saisonnier : f dépend uniquement de ν = 2π/P, la fréquence de mouvement moyen.

Dans un formalisme plus complet (c'est-à-dire sans linéarisation de la température), les deux effets sont couplés.

Ces force agissent sur le demi-grand axe de l'orbite de l'astéroïde. En moyennant ces petites perturbations sur une révolution, on a :

,

,

où est le coefficient de pression de radiation, R' = R / l_ν une longueur normalisée, et F_ν la fonction définie comme suit:

.

Les paramètres K_i(R') sont des fonctions analytiques de R'. La dernière équation est la même pour les deux effets Yarkovsky, en remplaçant ν = ω pour l'effet diurne, et ν = ν_mm pour l'effet saisonnier. On peut remarquer que le paramètre Θ_ν est le paramètre qui fait la plus grande différence entre les deux effets.

Les paramètres importants dans le changement du demi-grand axe par l'effet Yarkovsky sont donc :

• l'obliquité et la rotation : l'effet saisonnier produit toujours une diminution de a et est maximum à , alors que l'effet diurne peut produire une augmentation ( ) et une diminution () de a, et est maximum pour . De plus, l'effet Yarkovsky est négligeable dans la limite des rotations à vitesse infinie ou nulle car les variations de température sont nulles le long d'une même longitude.
• la taille : l'effet Yarkovsky est négligeable pour les très petits astéroïdes car l'onde thermique chauffe de la même manière toute sa surface (donc typiquement quand D est de l'ordre de l_ν), et pour les grands objets car la gravitation l'emporte (à partir de D égal à 20 kilomètres).
• conductivité thermique : pour les corps très poreux ou ayant une surface semblable au régolithe, κ est très faible (de l'ordre de 10^-3 W·m^-1·lK^-1). Pour les corps rocheux (chondrites ou glace), κ est intermédiaire (1 W·m^-1·lK^-1), alors que pour les corps ferreux κ est très élevé (40 W·m^-1·lK^-1). Les variations de κ modifient les paramètres l_ν et Θ_ν : un κ petit implique que , et donc et l'effet Yarkovsky disparaît ; un κ grand implique que et , et donc , ce qui correspondà un équilibre thermique de l'astéroïde.
• distance au Soleil : l'effet Yarkovsky diminue quand la distance de l'astéroïde au Soleil augmente.

Les valeurs caractéristiques de changement du demi-grand axe sont de l'ordre de 0,1 unité astronomique pour les objets sub-kilométriques, et d'environ 0,01 ua pour les objets de diamètre supérieur au kilomètre. Par ailleurs, le paramètre κ a de moins en moins d'importance au fur et à mesure que la taille de l'astéroïde augmente.

Ainsi, l'effet Yarkovsky est le premier mécanisme pour les astéroïdes ayant un diamètre inférieur à 20 kilomètres qui leur permette d'échapper à la ceinture principale et est susceptible de les amener sur des orbites de type géocroiseur.

Outre le changement du demi-grand axe, qui est l'effet le plus important et le plus prononcé de l'effet Yarkovsky, celui-ci se traduit aussi par des changements de l'excentricité et l'inclinaison de l'orbite de l'astéroïde.