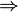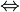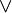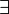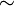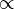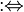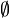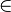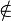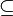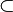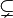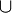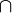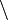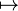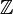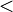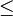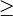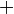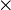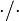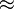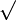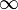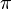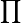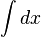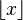Table des symboles mathématiques français-anglais - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
En mathématiques, certains symboles sont fréquemment utilisés. Le tableau suivant représente une aide pour les non-mathématiciens qui ne sont pas habitués à ces symboles. Dans la table, sont précisés pour chaque symbole, le nom, la prononciation et la branche des mathématiques dans laquelle le symbole est principalement utilisé.
Du fait de la grande variété des utilisations pour certains symboles, le tableau ne saurait prétendre à l'exhaustivité.
| Symbole (TeX) | Symbole (utf8) | Nom | Name |
|---|---|---|---|
| Prononciation | Read as | ||
| Branche | Category | ||
|
| ⇒ | Implication | (name) |
| « implique » ou « si... alors » | (read as) | ||
| Logique | (category) | ||
|
| ⇔ | Équivalence logique | |
| « si et seulement si » ou « équivaut à » | |||
| Logique | |||
|
| ∧ | Conjonction logique | |
| « et » | |||
| Logique | |||
|
| ∨ | Disjonction logique | |
| « ou » | |||
| Logique | |||
|
| ¬ | Négation logique | |
| « non » | |||
| Logique | |||
|
| ∀ | Quantificateur universel | |
| « Quel que soit », « pour tout » | |||
| Logique | |||
|
| ∃ | Quantificateur existentiel | |
| « il existe au moins un ... tel que » | |||
| Logique | |||
|
| ~ | Relation d'équivalence | |
| « ... est équivalent à ... » | |||
| théorie des ensembles | |||
| équivalence | |||
| « ... est équivalent à ... » | |||
| Analyse | |||
| Distribution de probabilité | |||
| « ... a la distribution de probabilité ... » | |||
| Statistiques | |||
|
| = | égalité | equality |
| « est égal » | is equal to; equals | ||
| toute branche | everywhere | ||
|
| ∝ | Proportionnalité | |
| « est proportionnel à » | |||
| toute branche | |||
| : = | := :⇔ | Définition | |
| « est défini comme » | |||
| très peu utilisés | |||
| {,} | { , } | Ensemble en extension | |
| « L'ensemble des ... » | |||
| Théorie des ensembles | |||
| { / } {;} {} | { / } { ; } { } | Construction d'ensemble en compréhension | |
| « L'ensemble de tous les ... qui vérifient ... » | |||
| Théorie des ensembles | |||
|
{} | ∅ {} | Ensemble vide | |
| « Ensemble vide » | |||
| Théorie des ensembles | |||
|
| ∈ ∉ | Appartenance (ou pas) à un ensemble | |
| « appartient à », « est élément de », « est dans ». « n'appartient pas », « n'est pas élément de », « n'est pas dans » | |||
| Théorie des ensembles | |||
|
| ⊆ ⊂ | Sous-ensemble | |
| « est un sous-ensemble (une partie) de ... », « est inclus dans... » | |||
| Théorie des ensembles | |||
|
| ⫋ | Sous-ensemble strict, partie stricte | |
| « est un sous-ensemble strict de ... », « est strictement inclus dans... » | |||
| Théorie des ensembles | |||
|
| ∪ | Réunion | |
| « Réunion de ... et de ... », « ... union ... » | |||
| Théorie des ensembles | |||
|
| ⋂ | Intersection | |
| « Intersection de ... et de ... », « ... inter ... » | |||
| Théorie des ensembles | |||
|
| \ | Différence | |
| « différence de ... et ... », « ... moins ... », « ... privé de ... » | |||
| Théorie des ensembles | |||
| () [] {} | ( ) [ ] { } | Fonction application; regroupement | |
| « de » | |||
| toute branche | |||
|
| → | Fonction | |
| « de ... vers », « de ... dans », « de ... sur ... » | |||
| toute branche | |||
|
| ↦ | Fonction | |
| « est envoyé sur », « a pour image » | |||
| toute branche | |||
|
| ℕ | Ensemble des entiers naturels | |
| « N » | |||
| Nombre | |||
|
| ℤ | Ensemble des entiers relatifs | |
| « Z » | |||
| Nombre | |||
|
| ℚ | Ensemble des nombres rationnels | |
| « Q » | |||
| Nombre | |||
|
| ℝ | Ensemble des nombres réels | |
| « R » | |||
| Nombre | |||
|
| ℂ | Ensemble des nombres complexes | |
| « C » | |||
| Nombre | |||
 | < > | Comparaison | |
| « est strictement inférieur à », « est strictement supérieur à » | |||
| Relation d'ordre | |||
|
| ≤ ou ⩽ ≥ ou ⩾ | Comparaison | |
| « est inférieur à », « est inférieur ou égal à »; « est supérieur à », « est supérieur ou égal à » | |||
| Relation d'ordre | |||
|
| + | Addition | |
| « plus » | |||
| Arithmétique | |||
|
| - | Soustraction | |
| « moins » | |||
| Arithmétique | |||
|
| × | Multiplication | |
| « fois » | |||
| Arithmétique | |||
|
| ÷ | Division | |
| « divisé par » | |||
| Arithmétique | |||
|
| / | fraction | |
| « sur » | |||
| Arithmétique Nombre | |||
|
| ≈ | Approximation | |
| « approximativement égal à » | |||
| Nombre réel | |||
|
| √ | Racine carrée | |
| « Racine carrée de ... » | |||
| Nombre | |||
|
| ∞ | Infini | |
| « Infini » | |||
| Nombre | |||
|
| π | π | |
| « Pi » | |||
| Géométrie euclidienne | |||
|
| | | | Valeur absolue ou module d'un nombre complexe ou cardinal d'un ensemble | |
| « Valeur absolue de... », « module de ... »; « cardinal de ... » | |||
| Nombre ou Théorie des ensembles | |||
|
| ∑ | Somme | |
| « Somme de ... pour ... de ... à ... » | |||
| Arithmétique | |||
|
| ∏ | Produit | |
| « Produit de .. pour .. de .. à .. » | |||
| Arithmétique | |||
|
| ∫,∬,∭,∮,∯ ou ∰ | Intégrale | |
| « Intégrale (de .. à ..) de .. d-.. » | |||
| Analyse | |||
|
|
| Partie entière | |
| « Partie entière de .. » | |||
| Partie entière |