Théorème d'Abel (algèbre) - Définition

• Si G est abélien alors il existe une base de L considérée comme un espace vectoriel sur K de radicaux de K.

L'extension L est un corps de décomposition séparable. L'article sur les corps de décomposition démontre que L est une extension de Galois finie. En conséquence G contient exactement n éléments, et un élément laissé invariant par chaque élément de G appartient nécessairement à K (cf deuxième proposition du paragraphe sur les propriétés élémentaires.

Le groupe de Galois est aussi une représentation de groupe dans l'espace vectoriel L, chaque élément du groupe m étant maintenant considéré comme un automorphisme d'espace vectoriel. Dans le cas de la représentation d'un groupe fini abélien dans un espace vectoriel de dimension finie, alors il existe une base qui diagonalise chaque automorphisme du groupe. Chaque valeur propre est racine de l'équation X ⁿ - 1 = 0, d'après le théorème de Lagrange. Une valeur propre est donc une racine n-ième de l'unité.

Soit (r₁, ..., r_n) une base qui diagonalise tous les éléments de G, et (λ₁, ..., λ_n) les valeurs propres associées à m un élément quelconque de G alors:

Or L est une extension de Galois, en conséquence, r_iⁿ, laissé invariant par chacun des automorphismes du groupe, est un élément de K. Ce qui démontre que la base choisie est une base de radicaux. La proposition est donc démontrée.

• Si G est un groupe résoluble, alors tout élément de L possède une expression par radicaux sur K.

Dire que G est résoluble signifie qu'il existe une suite finie de k + 1 sous-groupes de G telle que :

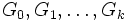
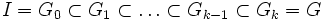
Où, si i est compris entre 0 et k - 1 G_i est un sous-groupe distingué de G_{i + 1} et le groupe quotient G_{i + 1} / G_i est abélien. Ici, I désigne le groupe réduit à l'élément neutre. Démontrons alors la proposition par récurrence sur k.

Si k est égal à 1, alors le groupe de Galois de L est abélien. En conséquence il existe une base L formée par des radicaux de K. Toute racine s'exprime dans cette base, ce qui démontre la proposition.

Supposons la propriété vraie à l'ordre p et supposons que k est égal à p + 1.

Considérons alors le corps L_k-1 choisi comme étant égal aux élements de L laissé invariant par tous les automorphismes de G₁. Alors le théorème fondamental de la théorie de Galois assure que L_k-1 est une extension de Galois dont le groupe de Galois est isomorphe à G / G₁. Cette extension vérifie donc l'hypothèse de récurrence et tous ses éléments s'expriment par radicaux sur K.

Le théorème fondamental assure aussi que L est une extension de Galois sur L_k-1 ayant comme groupe de Galois le groupe abélien G₁. Donc tout élément de L s'exprime par radicaux sur L_k-1 et donc sur K. Et la proposition est démontrée.

• Existence de la suite d'extensions (L_i).

On remarque, dans une premier temps que tout radical s'écrit comme composé de radicaux dont l'ordre est un nombre premier, car:

Soit R l'ensemble des radicaux d'ordre un nombre premier utilisés dans les définitions des différentes racines de P[X]. R est un ensemble fini, notons k son cardinal. Notons F l'extension du corps K engendrée par R. Montrons alors par récurrence sur k l'existence de la suite d'extensions.

cas où k est égal à 1.

R ne contient qu'un seul élément α₁ et la suite définie par F₀ = K et F₁ = K(α₁) = F vérifie la proposition.

Supposons la propriété démontrée à l'ordre m et supposons que k soit égal à m + 1.

Comme R est l'ensemble des radicaux d'ordre un nombre premier utilisé dans l'expression des racines, il contient au moins un élément α₁ qui est un radical de K. Soit F₁ = K(α₁), F est une extension de F₁ engendrée par m éléments. Il existe par hypothèse de récurrence une suite:

L'adjonction de K à cette suite démontre la proposition.

• Si F_i est un corps contenant une racine primitive p-ième de l'unité où p est un nombre premier, si α est un élément de Ω tel que α^p est élément de F_i, alors F_i(α) est une extension abélienne.

Montrons que F(α) est une extension séparable.

Notons r une racine primitive p-ième de l'unité. Si α est un élément de F alors la proposition est évidente. Dans le cas contraire, X^p - α^p est un polynôme annulateur de α. Ce polynôme est séparable car ses racines sont de la forme r^k. α ou k est un entier compris entre 1 et p, et elles sont toutes distinctes. Le polynôme minimal de α est un diviseur du polynôme précédent, il est donc séparable. En conclusion le théorème de l'élément primitif montre que l'extension F(α) est séparable.

Montrons que F(α) est une extension normale.

F(α) est engendré par la famille 1,α, ..., α^p-1 elle est donc de dimension inférieure ou égale à p. Tout morphisme m de F(α) dans la clôture algébrique de K est défini exactement par sa valeur en α. Cette valeur est une racine du polynôme X^p - α^p et il existe donc k tel que m(α) = r^k α. Réciproquement toute valeur entière k comprise entre 0 et p - 1 définit un morphisme. Tous ses p morphismes distincts laissent F(α) stable. Ce qui montre que F(α) est une extension normale.

Montrons que F(α) est une extension abélienne.

L'extension est normale et séparable, elle est donc galoisienne. Il suffit de remarquer que le groupe de Galois a pour ordre un nombre premier pour conclure que ce groupe est cyclique, donc abélien.

• Si P[X] est résoluble, alors son groupe de Galois l'est.

Montrons par récurrence sur k que F_i est une extension galoisienne de K.

Si k est égal à 1, alors F est égal à K(α) et la proposition précédente démontre que F est une extension galoisienne de groupe un groupe abélien donc résoluble.

Supposons la propriété vraie pour m et supposons de k = m + 1.

Alors F_k-1 est une extension galoisienne de K, F est une extension galoisienne de F_k-1 d'après le résultat précédent. On en déduit que F est une extension galoisienne de K. Soit G_i où i est un entier compris entre 0 et k le sous-groupe du groupe G de Galois de F laissant invariant F_i. Comme F_i est une extension galoisienne de K, G_i est un sous-groupe distingué de G et donc de G_i+1 si i est plus petit que k. La démonstration précédente montre que le groupe de Galois de l'extension F_i+1 de F_i est abélien, le quotient de G_i+1 par G_i isomorphe à ce groupe est donc aussi abélien. G est donc résoluble.

L'extension L de K est incluse dans F et est de Galois car c'est un corps de décomposition inclus dans une extension séparable. Le groupe H laissant invariant L est donc un sous-groupe distingué de F. G est résoluble, H est un sous-groupe distingué de G, donc G/H est résoluble (cf groupe résoluble). Or G/H est le groupe de Galois de L (cf théorème fondamental de la théorie de Galois). La proposition est ainsi démontrée.