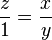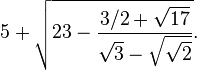Nombre constructible - Définition

Un nombre constructible à la règle et au compas est la mesure d'une longueur associée à deux points constructibles à la règle et au compas.

C'est du moins ainsi que le définissaient les mathématiciens grecs et tous ceux qui, à leur suite, ont cherché à déterminer quels étaient les points et les nombres constructibles de cette façon.

Du temps de la mathématique grecque, les seuls outils géométriques " autorisés " étaient la droite et le cercle. Toute construction faisant intervenir d'autres outils dit " mécaniques " (spirale d'Archimède, conchoïde, ellipse...) n'étaient que de la géométrie " abâtardie ". Cette vision très rigoriste de la géométrie euclidienne est à la source de problèmes célèbres comme l'irrationalité de racine de 2, la quadrature du cercle, la trisection de l'angle et la duplication du cube.

Les mathématiciens, jusqu'au XVII^e siècle n'accordaient aucune réalité concrète aux nombres négatifs. Il nous faudra cependant, pour maîtriser plus parfaitement la notion de nombre constructible, étendre la définition, non plus à des longueurs mais à des coordonnées de points constructibles.

Définition d'un nombre constructible

On donne ici une définition mathématique précise de la notion de point constructible (sous-entendu, à la règle et au compas). Remarquons que ni le vocabulaire intermédiaire introduit ni les notations ne sont classiques. On les a introduit pour décomposer proprement ce concept mathématique.

Points constructibles

Points constructible en 1 étape

Soit E un sous-ensemble du plan euclidien, qu'on assimile ici à . On dit qu'un point P = (x,y) est constructible en 1 étape à partir de E si, et seulement si, P est un point de E ou si P est dans l'intersection de deux objets quelconques parmi :

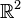
• l'ensemble des droites qui passent par deux éléments distincts de E ;
• l'ensemble des cercles centrés en un point de E et dont le rayon est la distance de deux quelconques points de E.

On note C₁(E) l'ensemble des points constructibles en 1 étape à partir de E.

On peut remarquer que si E est fini, alors, C₁(E) l'est aussi.

Points constructibles en n étapes

Partant des mêmes données, on définit, naturellement et par récurrence, l'ensemble C_n(E) des points constructibles en n étapes à partir de E. Pour n = 1, c'est la construction précédente. Sinon, on pose : .

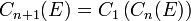
Points constructibles

Enfin, comme on s'y attend, l'ensemble des points constructibles à partir de E, qu'on note C(E), est la réunion (croissante) des C_n(E), c'est-à-dire : un point P est dit constructible à partir de E s'il en n étapes pour un certain n.

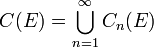
Nombres constructibles

On se place dans le même cadre, c'est-à-dire le plan euclidien assimilé à  ; on se donne E un sous-ensemble de .

Un nombre est dit constructible à partir de E si c'est l'abscisse ou l'ordonnée d'un point constructible à partir de E.

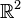
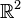
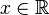
Un nombre constructible (tout court) est un nombre constructible à partir de l'ensemble .

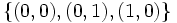
Rappel sur quelques constructions possibles

A l'aide d'une règle et d'un compas, on peut construire des cercles et des droites, bien sûr, mais aussi des parallèles et des perpendiculaires :

Parallèle

On construit le quatrième point d'un parallélogramme ABCX en traçant un arc de cercle de centre C et de rayon BA et un arc de cercle de centre A et de rayon BC.

Perpendiculaire

On utilise les propriétés des symétries axiales.

Opération sur les nombres constructibles

Addition

Soustraction

À condition que x > y

Multiplication

Une simple utilisation du théorème de Thalès permet de dire que 1×z = x × y

Division

La même utilisation du théorème de Thalès permet de dire que

Ces observations permettent de dire que l'ensemble des nombres constructibles (si on accepte les distances négatives) est un corps commutatif. Les Grecs ont ainsi pu établir que tous les nombres rationnels positifs étaient constructibles. Mais leur première surprise est venue de la dernière opération.

Extraction de racine carrée

On utilise le fait que, dans un triangle rectangle en A, si H est le pied de la hauteur issue de A, on a

BH×BC = BA²

(c'est une conséquence immédiate du fait que les triangles ABC et HAB sont semblables) et la propriété du triangle rectangle inscrit dans un demi-cercle, on peut extraire une racine carrée:

On trace donc la longueur x = BC, puis le cercle de diamètre BC, puis le point H tel que BH = 1, puis la perpendiculaire à (BC) menée par H, puis le point A intersection de cette perpendiculaire avec le cercle. BA² = 1×x nous assure que

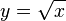
Les racines carrées sont donc constructibles. La première tentative des Grecs a été de dire que ces nombres étaient rationnels mais une démonstration simple leur a permis de se convaincre que cela n'était pas le cas. Il existait donc des nombres constructibles qui n'étaient pas rationnels mais irrationnels. Quelles étaient alors leur forme? Permettaient-ils de tout mesurer dans le monde réel ? Malgré leurs recherches, ils ne purent venir à bout du problème, ni eux ni les mathématiciens de langue arabe qui suivirent et qui eurent pourtant l'intuition du résultat.

Ensemble des nombres constructibles

Les opérations précédentes permettent donc de dire que tout rationnel est constructible, mais aussi que la racine carrée d'un rationnel est constructible et même que l'on peut, avec de la patience, construire le nombre suivant:

L'intuition semble dire que les seuls nombres constructibles sont ceux pouvant s'écrire uniquement à l'aide des 5 opérations précédentes. Il faut attendre les travaux de Pierre-Laurent Wantzel, qui, grâce aux travaux de Gauss sur les polygones constructibles, peut énoncer son théorème de Wantzel et affirmer que les seuls nombres constructibles sont ceux de cette forme (plus exactement sont dans une extension quadratique d'une extension quadratique d'une... d'une extension quadratique de Q). Une telle construction s'appelle une tour d'extension quadratique.

On peut exprimer ce résultat différemment : l'ensemble des nombres constructibles (à la règle et au compas) est le plus petit corps stable par racine carrée.

Grâce à ce théorème, tombent deux des problèmes de l'antiquité : la trisection de l'angle et la duplication du cube, qui reviennent à résoudre une équation de degré 3 (donc extension impaire). L'ensemble des nombres constructibles ne regroupe donc qu'une petite partie de l'ensemble des nombres algébriques. L'article tour d'extension quadratique propose une démonstration rigoureuse de ces résultats.

Le problème de la quadrature du cercle tombera un peu plus tard, quand Ferdinand von Lindemann aura prouvé en 1882 que π n'est pas algébrique, c’est-à-dire n'est solution d'aucune équation de degré n à coefficients dans Q. le nombre π ne peut donc pas se trouver dans une extension quadratique d'une extension quadratique d'une... d'une extension quadratique de Q.

Variantes de constructibilités et liens avec la constructibilité à la règle et au compas

Constructibilité uniquement au compas

Le théorème de Mohr-Mascheroni, montré par Georg Mohr, puis par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul.

Voir aussi le problème de Napoléon qui consiste à construire au compas seul le centre d'un cercle donné,
ainsi que la construction du carré au compas seul.

(à remplir, c'est fait dans le Carrega)

Constructibilité uniquement à la règle

Des points de bases étant donnés, un point est constructible à la règle s'il est point d'intersection de deux droites, chacune de ces deux droites passant par deux points qui sont des points de base ou des points déjà construits.

Les propriétés d'une figure constructible sont conservés par projection centrale. Ce n'est pas le cas pour les milieux où les parallèles ou les symétries.

Il est démontré qu'il impossible avec uniquement une règle de construire le milieu d'un segment, de mener par un point une parallèle à une droite.

D'après l'ouvrage de Carrega J.-C. - Théorie des corps : la règle et le compas - Hermann 2001 ; où l'on trouvera les démonstrations.

Exemples de constructions à la règle seule.

À lire

Jean Claude Carréga: Théorie des corps, la règle et le compas . Hermann 1981

Articles de mathématiques en rapport avec la notion de nombre

Définition des nombres · Entiers naturels · Entiers relatifs · Nombres transfinis  · Nombres décimaux · Nombres rationnels · Nombres constructibles · Nombres algébriques · Nombres transcendants · Nombres calculables · Nombres réels · Nombres complexes · Nombres hypercomplexes · Quaternions · Octonions · Sédénions · Nombres hyperréels · Nombres surréels · Nombres ordinaux · Nombres cardinaux · Nombres p-adiques · Nombres normaux · Suite d'entiers · Constantes mathématiques · Grands nombres · Nombres incalculables · Infiniments petits · Infini