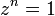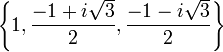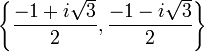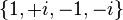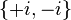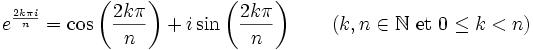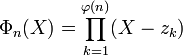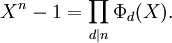Racine de l'unité - Définition
En mathématiques, étant donné un nombre entier naturel non nul n, une racine n-ième de l'unité (parfois appelée nombre de de Moivre du nom d'Abraham de Moivre) est un nombre complexe dont la puissance n-ième vaut 1. Pour un entier n donné, toutes les racines n-ième de l'unité sont situées sur le cercle unité et sont les sommets d'un polygone régulier à n côtés ayant un sommet d'affixe 1.
L'expression " racine n-ième " n'a pas valeur de norme, elle provient de l'habitude qu'ont les mathématiciens, souvent, de nommer un entier naturel n. Si l'entier en question est noté p, on parlera de " racine p-ième ", etc.
Définition
Pour un entier naturel non nul n donné, on appelle racine n-ième de l'unité toute solution complexe de l'équation
d'inconnue z. Il existe exactement n racines n-ièmes de l'unité. Les racines n-ièmes de l'unité forment un groupe cyclique d'ordre n pour la multiplication des nombres complexes avec 1 comme élément neutre.
Chaque racine du groupe a pour ordre l'entier d défini comme le plus petit entier strictement positif tel que
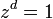
Exemples
Les racines troisièmes (ou cubiques) de l'unité sont
Les racines primitives troisièmes de l'unité sont
La première est habituellement notée j et la seconde, son conjugué,
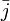
Les racines quatrièmes de l'unité sont
Les racines primitives quatrièmes de l'unité sont
Propriétés
Expression complexe
Le racines n-ièmes de l'unité peuvent s'écrire sous la forme
Lorsque l'entier n est supérieur ou égal à 2, la somme de ces nombres est égale à 0, un fait simple qui est souvent utile en mathématiques. Il peut être démontré de différentes manières, par exemple en reconnaissant une somme d'une progression géométrique.
Les racines primitives n-ièmes de l'unité sont exactement les nombres de la forme
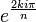
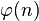

Polygones réguliers
Dans le plan complexe, les points dont les affixes sont les racines n-ièmes de l'unité sont les sommets du polygone régulier à n côtés inscrit dans le cerlce de centre O (le point d'affixe zéro) et de rayon 1.
L'étude de ces nombres, grâce aux puissants outils de l'algèbre, facilite donc celle, beaucoup plus ancienne, des polygones réguliers.
Polynôme cyclotomique
Article détaillé: Polynôme cyclotomique
Les racines n-ièmes de l'unité sont précisément les racines du polynôme
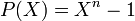
où
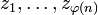
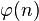
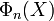
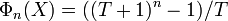
Chaque racine n-ième de l'unité est une racine primitive d-ième de l'unité pour exactement un diviseur positif de n. Cela implique que
Cette formule représente la décomposition du polynôme
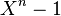
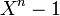
Corps cyclotomiques
Article détaillé: Polynôme cyclotomique
En adjoignant une racine primitive n-ième de l'unité à

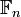

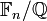
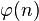
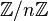
Comme le groupe de Galois de
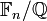
Réciproquement, chaque extension abélienne du corps des nombres rationnels est un sous-corps d'un corps cyclotomique - un théorème de Kronecker, habituellement appelé le théorème de Kronecker-Weber parce que Weber en a établi la démonstration.