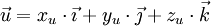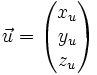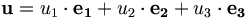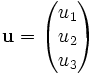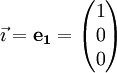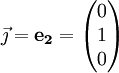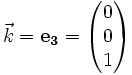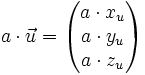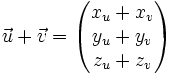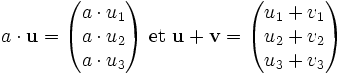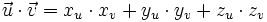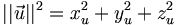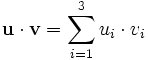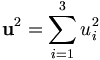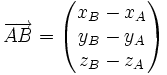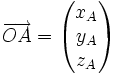Base (algèbre linéaire) - Définition

En algèbre linéaire, une base est une famille de vecteurs, qui, de manière simpliste, peut se voir comme une manière de se repérer dans l'espace en définissant des axes gradués. De manière plus rigoureuse, c'est une famille de vecteurs libre et génératrice. Voir les articles géométrie vectorielle et espace vectoriel.

Définition

Une famille de vecteurs forme une base si aucun de ces vecteurs ne peut se déduire des autres par une combinaison linéaire (une telle famille est dite " libre "), et si tout vecteur de l'espace peut s'exprimer comme une combinaison linéaire des vecteurs de la base (une telle famille est dite génératrice).

Dans le plan, une base est donc formée de deux vecteurs non colinéaires (non proportionnels) ; ces vecteurs sont souvent notés ou (e₁,e₂). Dans l'espace, il s'agit de trois vecteurs non coplanaires ; ces vecteurs sont souvent notés ou (e₁,e₂,e₃).

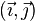
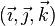
Plaçons-nous dans l'espace. Un vecteur quelconque peut donc s'écrire

où x_u, y_u et z_u sont des réels, nommés " coordonnées " ou " composantes " du vecteur. Notons que cette décomposition est unique. On peut aussi écrire sous la forme d'une matrice-colonne :

On utilise aussi fréquemment une autre notation des composantes, qui va souvent de pair avec l'autre notation pour la base :

On a :

Types de base

La base est dite orthonormée si les trois vecteurs sont orthogonaux entre eux et si leur norme vaut 1. Elle est dite directe si

• dans le plan, l'angle — ou  — est positif
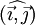
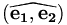
• dans l'espace, le trièdre formé par les trois vecteurs de la base est direct.

Les bases orthonormées directes sont les bases le plus souvent utilisées. Cependant, il est intéressant dans certains cas d'avoir une base " quelconque ". Par exemple, dans un cristal, l'organisation des atomes définit une base " naturelle " (la maille) qui n'est pas nécessairement orthonormée. De même, lorsque l'on étudie la déformation des solides, les axes permettant d'exprimer les équations de la manière la plus simple ne sont pas toujours orthogonaux.

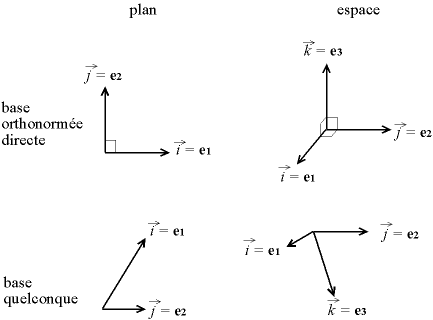
Base orthonormée directe et base quelconque, du plan et de l'espace

Opérations vectorielles et composantes

Les premières considérations concernent toutes les bases y compris les bases qui ne sont pas orthonormées directes.

Si (x_u,y_u,z_u) sont les composantes de et (x_v,y_v,z_v) sont celles de , alors on a :

et

ou avec l'autre notation

Une base orthonormée est particulièrement intéressante pour calculer le produit scalaire :

(ceci peut aussi se déduire du théorème de Pythagore). Avec l'autre notation, cela donne

Si de plus la base orthonormée est directe, cela simplifie le calcul du produit vectoriel. En effet, on a alors

 ;  ;

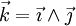
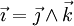
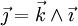
ou avec l'autre notation

 ;  ;

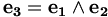
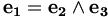
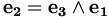
Il suffit alors de mettre côte à côte les deux matrices-colonne représentant les vecteurs, de rajouter une quatrième ligne comprenant la première composante (x_u ou u₁), et de soustraire les produits en croix des lignes deux par deux ; le résultat est placé dans la ligne n'intervenant pas dans le calcul. Par exemple le résultat du produit en croix entre les ligne x et y (les lignes 1 et 2) est placé dans la ligne z (ligne 3) de la matrice-colonne résultante.

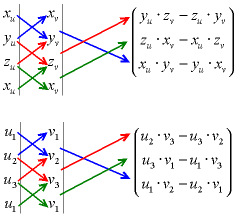
Algorithme permettant de calculer simplement le produit vectoriel dans le cas d'une base orthonormée directe

Voir aussi : Géométrie analytique.

Base et repère

Un repère (du plan ou de l'espace) est la donnée d'une base et d'un point de référence, noté en général O. Nous allons supposer ici que la base utilisée pour les vecteurs est la même que celle utilisée pour le repère. Si les coordonnées du point A sont (x_A,y_A,z_A) et celles du point B sont (x_B,y_B,z_B), alors le vecteur a pour composantes :

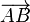
en particulier, on a

En utilisant l'autre notation, les coordonnées de A sont (a₁,a₂,a₃) et celles du point B sont (b₁,b₂,b₃), et le vecteur u = AB a pour composantes :

u_i = b_i - a_i

Les transformations

Les transformations d'une base sont toujours l'inverse de celles des fonctions qui y sont décrites. Par exemple, la rotation d'un repère dans le sens trigonométrique est équivalente à la rotation des vecteurs dans le sens horaire.