Anneau de Dedekind - Définition

Histoire

Premiers essais

Leonhard Euler utilise pour la première fois un anneau d'entiers algébriques.

L'histoire initiale de l'étude des anneaux de Dedekind se confond avec celles des entiers algébriques. En 1753, Leonhard Euler écrit à Goldbach qu'il a trouvé une preuve du dernier théorème de Fermat pour n égal à trois. Elle se fonde sur l'utilisation de l'anneau des nombres de la forme a + b.i√3 où a et b sont des entiers relatifs et i l'unité imaginaire. La preuve s'avère fausse car, contrairement à ce qu'imagine le mathématicien, un tel anneau n'est pas factoriel c'est-à-dire qu'il n'existe pas une unique décomposition en facteurs premiers, un contre exemple est donné par les deux décompositions suivantes :

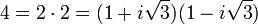
Si l'application est encore approximative, l'utilisation d'ensemble de nombres de cette nature s'avère fructueuse. Carl Friedrich Gauss étudie les nombres de la forme a + i.b permettant, par exemple de fournir des preuves élégantes du théorème des deux carrés de Fermat, ils sont maintenant dénommés entiers de Gauss. Ferdinand Eisenstein analyse l'anneau des entiers portant son nom et qui offre une démonstration rigoureuse du grand théorème de Fermat pour n égal à trois analogue à celle d'Euler.

Groupe des unités

Dirichlet établit le théorème clé associé aux unités d'un anneau d'entiers.

La résolution générale du dernier théorème de Fermat amène l'étude d'autres anneaux d'entiers. Johann Peter Gustav Lejeune Dirichlet comprend que, pour les valeurs supérieures de n, une première obstruction rend la démonstration plus technique. Il utilise l'anneau maintenant appelé des entiers de Dirichlet formé des nombres de la forme a + b.1/2 (1 + √5). L'obstruction réside dans le fait que, si l'anneau est bien euclidien, l'ensemble des éléments inversibles encore appelé groupe des unités devient infini. Pour ces éléments, aucun outil classique de la théorie des anneaux, comme la décomposition en facteurs premiers n'est possible. Il parvient néanmoins à trouver une preuve complétée quelques mois plus tard par Adrien-Marie Legendre .

Cette analyse du groupe des unités dans le cas d'entiers quadratiques revient à l'étude de la structure des solutions de l'équation de Pell-Fermat. Une élucidation générale de la structure du groupe des unités d'une fermeture intégrale est finalement donnée par Dirichlet et porte maintenant le nom de théorème des unités de Dirichlet.

La compréhension de la structure du groupe des unités ne permet néanmoins pas de venir à bout du dernier théorème de Fermat. Gabriel Lamé prouve bien, quatorze ans après Dirichlet, l'absence de solution pour n égal à sept à l'aide d'un anneau entiers quadratique comportant un groupe des unités infini. Cependant la preuve est complexe et non généralisable.

Deuxième obstruction

Ernst Kummer comprend comment contourner la deuxième obstruction.

Lamé croit trouver une solution générale en utilisant l'anneau des entiers d'un corps cyclotomique. Un corps cyclotomique d'indice n est le plus petit corps contenant les racines n^ième de l'unité du corps des complexes. L'anneau des entiers est celui des nombres du corps racine d'un polynôme unitaire à coefficients entiers relatifs. Son erreur consiste à supposer, en terme moderne que l'anneau est factoriel, c'est-à-dire que le théorème fondamental de l'arithmétique s'applique sur une structure de cette nature.

Cette propriété, que l'on sait être fausse dans le cas général pour les anneaux d'entiers quadratiques n'est pas non plus vérifiée pour les entiers cyclotomiques. En 1844, soit trois ans plus tôt, Ernst Kummer avait établi cette absence de propriété dans le cas général en exhibant un contre exemple, les entiers du corps cyclotomiques des racines 23^ièmes de l'unité.

L'absence de factorialité de ce type d'anneau est, à la suite de Kummer, considérée comme la deuxième obstruction pour les anneaux de cette nature. Une manière d'interpréter cette difficulté consiste à considérer qu'il manque des nombres pour assurer l'unicité de la décomposition en facteurs premiers. Kummer définit des nombres idéaux palliant les manques et permettant d'exprimer une nouvelle forme de théorème fondamental de l'arithmétique. Elle lui permet de démontrer le dernier théorème de Fermat pour toute valeur de n jusqu'à 100 qui soit un nombre premier régulier, c'est-à-dire à l'exception de 37, 59 et 67 (parmi les nombres premiers < 100).

Formalisme de Dedekind

A l'instar de Leopold Kronecker l'objectif de Dedekind est de généraliser les résultats de Kummer à toute fermeture intégrale d'un corps de nombre et non pas seulement aux corps cyclotomiques. Leurs philosophies sont néanmoins opposées, l'objectif de Dedekind est en rupture avec la tradition calculatoire de Gauss et Kummer. Il cherche à démontrer les propriétés de ces anneaux à l'aide de leurs caractéristiques fondamentales et non pas le fruit de calculs complexes.

A cette occasion, il formalise la notion d'idéal et d'idéal principal. La multiplication des idéaux principaux correspond à celles de leurs générateurs et se généralise à tous les idéaux. L'objectif est alors de montrer que tout idéal se décompose de manière unique en un produit d'idéaux premiers. Les nombres idéaux de Kummer conduisent aux idéaux premiers non principaux. Un outil essentiel est l'idéal fractionnaire qu'il formalise en 1876. Elle confère à l'ensemble des idéaux une structure de groupe abélien dont un sous-groupe est composé des idéaux fractionnaires principaux et permet d'exprimer le théorème fondamental sur la structure des idéaux premiers non principaux : Le groupe quotient des idéaux fractionnaires par les idéaux fractionnaires principaux est fini dans le cas d'une fermeture intégrale d'un corps de nombres algébriques. Ce groupe quotient est appelé groupe des classes d'idéaux. Il démontre ce résultat dans toute sa généralité à la fin du siècle.

XX^e siècle

A la différence des anneaux principaux, les cas d'anneaux de Dedekind sont finalement fréquents. De plus, ils ne se limitent pas aux fermetures intégrales d'extension de corps. Un vaste sujet utilise largement cette structure : la géométrie algébrique. Les entiers relatifs sont remplacés par un anneau de polynômes sur un corps fini et le corps de nombre par un corps de fonctions. Un tel anneau vérifie encore les axiomes de Dedekind.

De nouveaux outils comme la valuation sont développés et les anneaux de valuation discrète permettent d'étudier de nouvelles structures comme les nombres p-adiques.