Anneau de Dedekind - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Idéal fractionnaire
Une propriété essentielle d'un anneau de Dedekind réside dans le fait que tout idéal non nul se décompose de manière unique en un produit d'idéaux premiers. Ce résultat est un substitut au théorème fondamental de l'arithmétique, qui ne s'applique que dans un anneau factoriel. Pour établir ces propriétés, il est utile de munir l'ensemble des idéaux d'une multiplication. Le produit de deux idéaux I1 et I2 est le plus petit idéal contenant tous les produits a.b si a (resp. b) est élément de I1 (resp. I2). Le produit est associatif, il admet un élément neutre (l'anneau tout entier) et est associatif. Il est alors commode d'enrichir l'ensemble de tous les inverses, la structure devenant ainsi un groupe abélien.
Les propriétés des idéaux et idéaux fractionnaires caractérisent un anneau de Dedekind. Plus précisément, le théorème suivant est présenté dans l'article détaillé :
Théorème — Soit A un anneau commutatif unitaire, les propriétés suivantes sont équivalentes :
- A est un anneau de Dedekind,
- tout idéal premier non nul de A est inversible,
- tout idéal non nul de A est inversible,
- A est intègre et tout idéal non nul de A est produit d'idéaux maximaux,
- A est intègre et tout idéal de A est produit d'idéaux premiers.
De plus, si A est un anneau de Dedekind, la décomposition de tout idéal non nul en produit d'idéaux premiers est unique (à l'ordre près des facteurs).
L'existence et l'unicité de la décomposition d'un idéal en idéaux premiers permet la définition (également présentée dans l'article détaillé) d'une famille de fonctions appelées valuations. La valuation en P, où P désigne un idéal premier non nul, est une fonction qui à un idéal non nul J de A associe le plus petit entier n tel que P n contienne J. Cette fonction est souvent notée : vP. Elle se prolonge sur les idéaux fractionnaires de A et prend alors ses valeurs dans l'ensemble des entiers relatifs. Si π désigne l'ensemble des idéaux premiers non nuls et F un idéal fractionnaire non nul :

La fonction qui à P associe vP(F) (pour F fixé) est nulle presque partout, c'est-à-dire que le produit précédent ne contient qu'un nombre fini de facteurs différents de A. Cette formule définit un isomorphisme entre le groupe des idéaux fractionnaires et le groupe abélien libre engendré par π.
À partir de cette fonction valuation sur les idéaux, on définit une valuation sur K, le corps des fractions de l'anneau de Dedekind A : pour un élément k, vP(k) est égal à l'image par vP de l'idéal fractionnaire principal kA. À chacune de ces valuations vP sur K est associé un anneau de valuation, et A est l'intersection de tous ces sous-anneaux de K.
Localisation
Une structure utile pour l'analyse d'un anneau de Dedekind est un anneau de fractions particulier.
Si P est un idéal premier d'un anneau commutatif unitaire intègre A, le localisé de A en P, noté AP, désigne l'ensemble des fractions a / b telles que a est élément de A et b un élément de A qui n'est pas dans P. C'est un anneau local : son unique idéal maximal est P.AP.
Si A est de Dedekind cet anneau AP est de plus un principal. C'est donc soit un corps si P est nul, soit un anneau de valuation discrète sinon. Comme les idéaux fractionnaires, la structure des localisés de A caractérise les anneaux de Dedekind, plus précisément:
Soit A un anneau commutatif unitaire intègre noethérien. Les propriétés suivantes sont équivalentes :
- A est de Dedekind,
- pour tout idéal maximal M, le localisé de A en M est un anneau principal,
- tout idéal premier non nul M est maximal et pour un tel M, le A/M-espace vectoriel M / M2 est de dimension 1.
Excluons le cas évident où A est un corps.
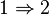
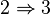
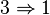
Extension finie
Une méthode pour construire un anneau de Dedekind est de considérer la fermeture intégrale d'un anneau de Dedekind A dans une extension finie de son corps des fractions K. C'est une généralisation du cas A=Z vu plus haut comme premier exemple, dans la .
-
- Soit L une extension finie séparable de K et B la fermeture intégrale de A dans L, alors B est un anneau de Dedekind, et son corps des fractions est L.
Le fait que B est un anneau commutatif, unitaire, intègre, noethérien, intégralement clos, et que son corps des fractions est L se démontre exactement comme dans le premier exemple, vu plus haut dans la (en remplaçant bien sûr Z par A et Q par K).
Pour conclure que B est de Dedekind, il reste à démontrer que tout idéal premier non nul P de B est maximal, c'est-à-dire que l'anneau quotient correspondant B / P est un corps.
Soit x un élément de B dont la classe
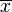
Or ce sous-anneau image n'est autre que C[
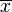
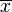
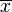
Soient
![\scriptstyle Q\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/e/e6d4b918f00d2bd04ad9016af95168da_f361c940750e3d420af6acb1c54cf7b4.png)
La séparabilité de L est utilisée, dans l'article Anneau noethérien, pour montrer que B est fini sur A (la forme trace de l'anneau B est non dégénérée, ce qui permet de montrer simplement le caractère fini de B, c'est-à-dire de type fini en tant que module sur A). Cet énoncé reste vrai pour toute extension finie L de K (non nécessairement séparable), cependant B ne sera plus nécessairement de type fini en tant que A-module.
L'étude des anneaux de Dedekind d'une extension de cette nature offre des outils d'analyse de la structure du corps L. La décomposition des idéaux premiers de K dans L permet de définir la ramification. Ce concept est utilisé, par exemple pour établir le théorème de Kronecker-Weber. La théorie des corps de classes généralise son usage.

















































