Histoire de la racine carrée - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Histoire des sciences |
| Chronologie |
|---|
| Chronologie des sciences |
| Chronologie de l'astronomie |
| Sciences de l'Antiquité |
| Sciences au Moyen Âge |
| XVe s. - XVIe s. |
| XVIIe s. - XVIIIe s. |
| XIXe s. - XXe s. |
| Thématiques |
| Sciences chinoises |
| Sciences grecques |
| Sciences indiennes |
| Sciences islamiques |
| Histoire... |
| de l'astronomie |
| des mathématiques |
| de la biologie |
| de la médecine |
| de la physique |
| de l'électricité |
| de la zoologie & botanique |
| de l'écologie |
| des sciences du langage |
| Voir aussi |
| Science |
| Histoire des sciences (discipline) |
| Philosophie des sciences |
| Épistémologie |
| Sociologie des sciences |
| Histoire des techniques |
| Méta |
| Projet |
L'histoire de la racine carrée commence autour du XXe siècle av. J.-C.. Sa première représentation connue date du XVIIe siècle av. J.-C.. La valeur de

Des mathématiciens ont rencontré ces problèmes depuis les débuts de l'écriture, en Mésopotamie (-1700), ils ont été fertiles jusqu'au du XIXe siècle, il conservent un intérêt pédagogique.
La racine carrée est une question classique d'histoire des sciences. Elle permet de tracer le fonctionnement réel des découvertes, de leur oubli ou de leur transmission. Certaines représentations limitent la compréhension (les obstacles épistémologiques), d'autres favorisent la spéculation (techniques, organisation sociale, religion, philosophie…) ; mais au-delà de son avancement, chaque société à sa manière de faire des mathématiques. Pour s'en rendre compte, rien ne vaut une citation d'époque, même traduite, pour découvrir des technicités différentes, et souvent très élaborées. La racine carrée est un objet mathématique très défini, qui permet un petit voyage dans l'espace et le temps par les traces qu'il a laissé.
Babylone
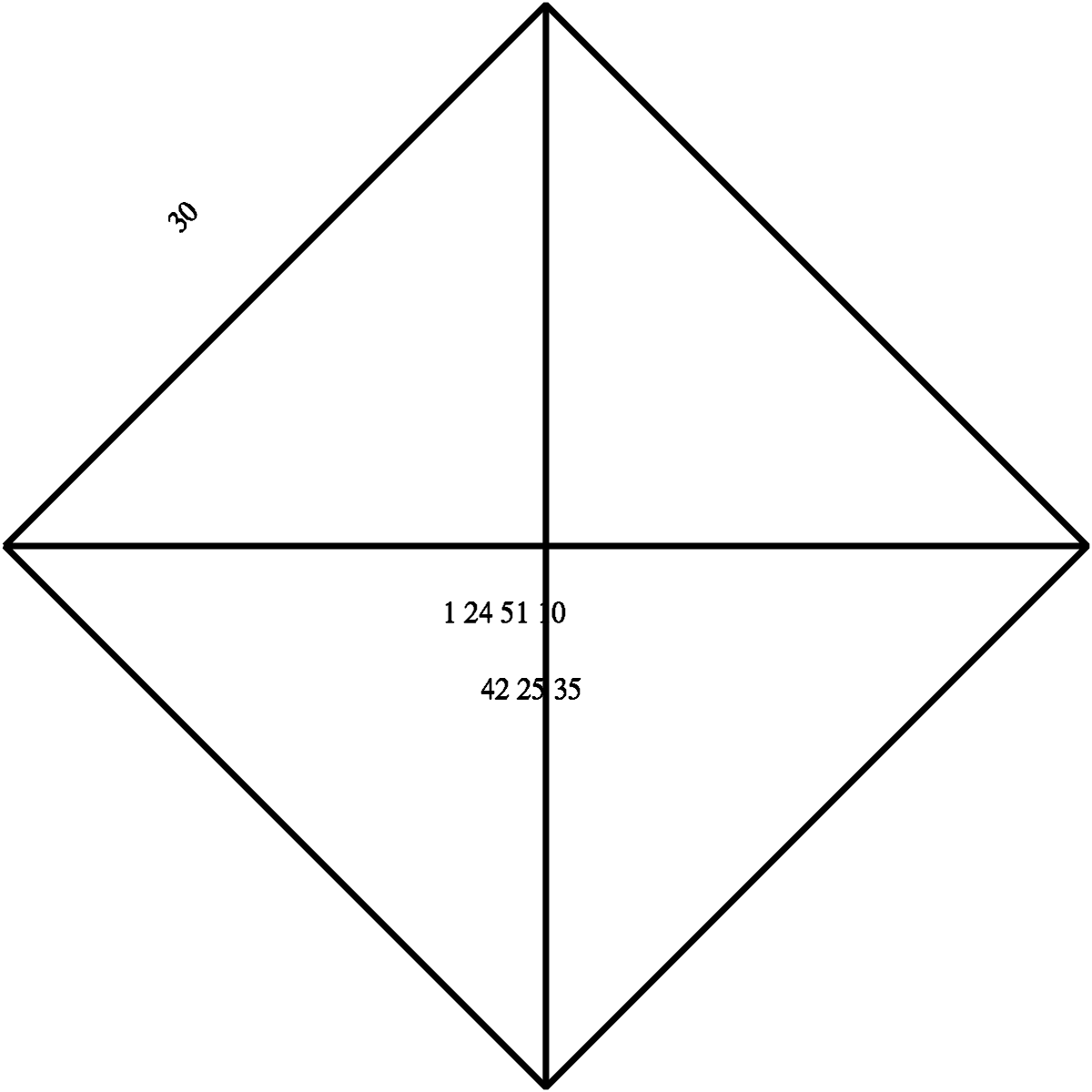
La première représentation connue d'une racine carrée est une tablette babylonienne YBC 7289 (-1800~-1600). On peut réellement affirmer que les mathématiques sont nées là. La photo est encore plus émouvante que le diagramme. On y reconnait distinctement un carré avec ses diagonales (d'autres tablettes confirment la construction). Le dessin est bâclé, avec des écritures que les spécialistes reconnaissent être celle d'un apprenti scribe : c'est un cahier d'exercices.
Les écritures sont des mesures, en particulier sur la diagonale. En système sexagésimal cunéiforme:
-
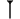
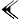
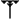
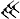
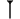
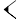
- 1 + 24/60 + 51/60² + 10/60 =~ 1,41421296
Une valeur approchée au six dix-millionièmes de √2 (6 décimales). Le calcul n'a pas été effectué sur la tablette. Le nombre a été selon toute vraisemblance dicté, ou appris, et appliqué avec à propos sur la figure. Des listes d'approximations ont ainsi été retrouvées. Mais comment ce nombre a-t-il été calculé ?
Il n'a pas encore été retrouvé de tablette expliquant exactement ce calcul pour √2. Toutefois, sur plusieurs autres problèmes (diagonale d'un rectangle, côtés de triangles, hexagones et autres polygones), des algorithmes itératifs sont bien utilisés. Les spécialistes acceptent l'hypothèse d'un genre de méthode de Héron. Cependant, la stricte application de celle-ci dans une notation sexagésimale ne permet pas de retrouver l'exacte approximation de la tablette YBC 7289. Il faut supposer la réutilisation d'approximations dans la simplification des calculs. De plus, les problèmes montrant l'utilisation de processus itératifs sont d'expression peu claire, mélangeant les unités, sans qu'il soit évident que le rédacteur à conscience que les étapes peuvent se répéter à l'infini.
L'exercice des mathématiques pour la majorité des scribes dont on retrouve les tablettes semble surtout consister à mémoriser des résultats exemplaires, établis par d'autres, et de savoir les utiliser à bon escient dans la variété des problèmes rencontrés. Toutefois, la précision atteinte dépasse l'utilité pratique, sans qu'on puisse y voir une motivation religieuse, peut-être est-elle librement spéculative, en tous cas pédagogique.

















































