Histoire de la racine carrée - Définition

Grèce antique

La Grèce connaît et même démontre l'irrationalité de √2, mais cette découverte est difficile à attribuer exactement.

Aristote (-384~-322) tient la démonstration pour acquise et l'utilise comme un exemple d'application du raisonnement par l'absurde et du tiers exclu, il dit juste : « la diagonale du carré est incommensurable à ses côtés, ou cela supposerait que les nombres impairs soient pairs. » (-335~-323), ses auditeurs sont censés connaître la démonstration arithmétique.

Si √2 était rationnel, il existerait donc par définition une fraction ou a et b sont entiers et irréductibles, . Quelle que soit la valeur de b², si a égal 2b², c'est qu'il est multiple de 2, donc pair. Or, si le carré de a est pair, alors a est pair. Ici est la disjonction pointée par Aristote, celle qui exclut une troisième option, le tiers exclus. Un nombre est ou pair ou impair. Si a est impair, , son carré est impair. Si a est pair, , son carré est pair. En conséquence, il existe un entier n, tel que , autrement dit, si a est pair, le carré de b est pair aussi. Comme pour a, si b² est pair, b doit être pair aussi. Là est le nœud du raisonnement, si a et b sont pairs, alors la fraction a/b peut être réduite par 2, ce qui est contradictoire à la définition initiale, donc la définition initiale est fausse, absurde, il n'existe pas de fraction rationnelle irréductible égale à √2. Le même raisonnement se montre pour √3 et les autres racines de nombres premiers[1].

 

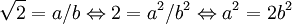
Platon(-427~-348) évoque un ensemble des racines dans le Théétète. L'action se tient après la mort de Socrate (-399), un tout jeune Euclide (-325~-265) rapporte un dialogue que Socrate aurait eu avec le mathématicien Théétète d'Athènes (-415 ~ -395 ou -369). Le sujet concerne la recherche d'un principe pour définir la science vraie. La définition des irrationnels est utilisée comme un exemple introductif du critère philosophique à chercher. Est aussi cité le mathématicien Théodore de Cyrène (-470~-420), maître de Platon.

L'incompatibilité des dates est évidente. Toutefois, c'est dans le style de Platon d'invoquer dans ses dialogues les figures représentatives d'un problème. Il veut clairement signifier que Théétète hérite de Théodore. Reste qu'Euclide n'était pas né quand Platon mourut. Plusieurs critiques ont voulu supposer un autre Euclide, avec autant de mémoire et de talents. La probabilité est faible. Une autre hypothèse s'accorde tout à fait avec la composition du texte, l'introduction d'Euclide est postérieure, après la mort du maître. On sait qu'avant de rejoindre Alexandrie, le mathématicien naquit à Athènes, et l'Académie restait un centre d'études mathématiques.

Ce court passage montre que les mathématiques d'alors s'appuient toujours sur des analogies géométriques, mais que le discours se poursuit sans recourir à des figures, en énoncés oraux concluants (voir la logique d'Aristote). Certains historiens des sciences parlent même de raisonnement arithmétique précurseur d'une démonstration algébrique. Euclide a donc recueilli une tradition déjà longuement élaborée dans son Livre X des éléments. Il en tire d'autres propositions, en particulier une méthode d'approximation des racines dite d'antiphérèse, ou soustraction réciproque. Les définitions 1 à 3 rappellent celles du Théétète, dans d'autres termes.

Euclide a donc reçu de Théétète la définition d'une classe de nombres incommensurables, ou irrationnels, les racines. Théétète a appris de Théodore la preuve de l'irrationalité des racines jusqu'à 17, probablement par démonstration géométrique. Mais d'où Théodore tient la démonstration pour la première, √2 ? Platon encore, considère la démonstration pour si élémentaire, qu'elle peut être expliquée à un esclave dans le Ménon (duplication du carré). Un néoplatonisme bien postérieur l'attribue à l'école pythagoricienne. Jamblique (250~325) estime qu'elle concerne le partage d'un segment en extrême et moyenne raison, le nombre d'or . Pappus d'Alexandrie (340) en parle pour la diagonale du carré (√2), de même Proclos (412~485). Jamblique ajoute une légende très belle, critiquée par Proclos, peut-être le premier (et le dernier ?) martyre mathématique.

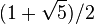
Hippase de Métaponte, disciple de Pythagore (v.-580~v.-490), connaissait l'incommensurabilité de √2 (peut-être découverte par son maître). La secte propageait une arithmétique mystique affirmant la rationalité de l'univers au sens mathématique, c’est-à-dire que le sensible est fait de grandeurs pouvant toutes se ramener à l'unité. L'existence d'au moins une seule grandeur irrationnelle prouvée, √2, réfute le principe métaphysique. Hippase aurait enfreint la règle de silence de la communauté, et révéler l'irrationalité du monde. Nous ne connaissons pas les enjeux théologiques de l'époque, mais Hippase a été banni, et peut-être d'avoir perdu l'amitié de ses frères, il se serait jeté à la mer.

Le néo-pythogoricien Théon de Smyrne (70~135), inspiré de la méthode d'antiphérèse d'Euclide, a utilisé le principe de suites encadrantes pour approcher la valeur de √2 (a/b, (a+2b)/(a+b) ... : 3/2, 7/5, 17/12 ...). Enfin Diophante d'Alexandrie (200/214~284/298) aura besoin d'une théorie des nombres unifiant les entiers, les rationnels et les irrationnels, pour la résolution d'une équation diophantienne.

Pour la Grèce antique, √2 est plus qu'un nombre. Ce fut d'abord un problème métaphysique, qui resta une introduction de choix à la philosophie (car « nul n'y entre s'il n'est géomètre »). La question parcoure un millénaire de culture classique, de Pythagore (-580~-490) à Proclos (412~485).