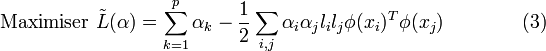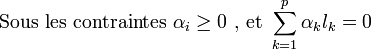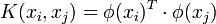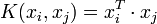Machine à vecteurs de support - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les machines à vecteurs de support ou séparateurs à vaste marge (en anglais Support Vector Machine, SVM) sont un ensemble de techniques d'apprentissage supervisé destinées à résoudre des problèmes de discrimination et de régression. Les SVM sont une généralisation des classifieurs linéaires.
Les SVM ont été développés dans les années 1990 à partir des considérations théoriques de Vladimir Vapnik sur le développement d'une théorie statistique de l'apprentissage : la Théorie de Vapnik-Chervonenkis. Les SVM ont rapidement été adoptés pour leur capacité à travailler avec des données de grandes dimensions, le faible nombre d'hyper paramètres, le fait qu'ils soient bien fondés théoriquement, et leurs bons résultats en pratique.
Les SVM ont été appliqués à de très nombreux domaines (bio-informatique, recherche d'information, vision par ordinateur, finance...). Selon les données, la performance des machines à vecteurs de support est de même ordre, ou même supérieure, à celle d'un réseau de neurones ou d'un modèle de mixture gaussienne.
Historique
Les séparateurs à vastes marges reposent sur deux idées clés : la notion de marge maximale et la notion de fonction noyau. Ces deux notions existaient depuis plusieurs années avant qu'elles ne soient mises en commun pour construire les SVM.
L'idée des hyperplans à marge maximale a été explorée dès 1963 par Vladimir Vapnik et A. Lerner, et en 1973 par Richard Duda et Peter Hart dans leur livre Pattern Classification. Les fondations théoriques des SVM ont été explorées par Vapnik et ses collègues dans les années 70 avec le développement de la Théorie de Vapnik-Chervonenkis, et par Valiant et la théorie de l'apprentissage PAC.
L'idée des fonctions noyaux n'est pas non plus nouvelle: le théorème de Mercer date de 1909, et l'utilité des fonctions noyaux dans le contexte de l'apprentissage artificiel a été montré dès 1964 par Aizermann, Bravermann et Rozoener.
Ce n'est toutefois qu'en 1992 que ces idées seront bien comprises et rassemblées par Boser, Guyon et Vapnik dans un article, qui est l'article fondateur des séparateurs à vaste marge. L'idée des variables ressorts, qui permet de résoudre certaines limitations pratiques importantes, ne sera introduite qu'en 1995. À partir de cette date, qui correspond à la publication du livre de Vapnik, les SVM gagnent en popularité et sont utilisés dans de nombreuses applications.
Un brevet américain sur les SVM est déposé en 1997 par les inventeurs originels.
Principe général
Les SVM peuvent être utilisés pour résoudre des problèmes de discrimination, c'est-à-dire décider à quelle classe appartient un échantillon, ou de régression, c'est-à-dire prédire la valeur numérique d'une variable. La résolution de ces deux problèmes passe par la construction d'une fonction h qui à un vecteur d'entrée x fait correspondre une sortie y :
- y = h(x)
On se limite pour l'instant à un problème de discrimination à deux classes (discrimination binaire), c'est-à-dire

Discrimination linéaire et hyperplan séparateur
Pour rappel, le cas simple est le cas d'une fonction discriminante linéaire, obtenue par combinaison linéaire du vecteur d'entrée
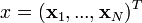
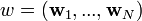
- h(x) = wTx + w0
Il est alors décidé que x est de classe 1 si
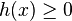
La frontière de décision h(x) = 0 est un hyperplan, appelé hyperplan séparateur, ou séparatrice. Rappelons que le but d'un algorithme d'apprentissage supervisé est d'apprendre la fonction h(x) par le biais d'un ensemble d'apprentissage :
-
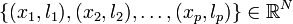
où les lk sont les labels, p est la taille de l'ensemble d'apprentissage, N la dimension des vecteurs d'entrée. Si le problème est linéairement séparable, on doit alors avoir :
Exemple
Prenons un exemple pour bien comprendre le concept. Imaginons un plan (espace à deux dimensions) dans lequel sont répartis deux groupes de points. Ces points sont associés à un groupe : les points (+) pour y > x et les points (-) pour y < x. On peut trouver un séparateur linéaire évident dans cet exemple, la droite d'équation y=x. Le problème est dit linéairement séparable.
Pour des problèmes plus compliqués, il n'existe en général pas de séparatrice linéaire. Imaginons par exemple un plan dans lequel les points (-) sont regroupés à l'intérieur d'un cercle, avec des points (+) tout autour : aucun séparateur linéaire ne peut correctement séparer les groupes : le problème n'est pas linéairement séparable. Il n'existe pas d'hyperplan séparateur.
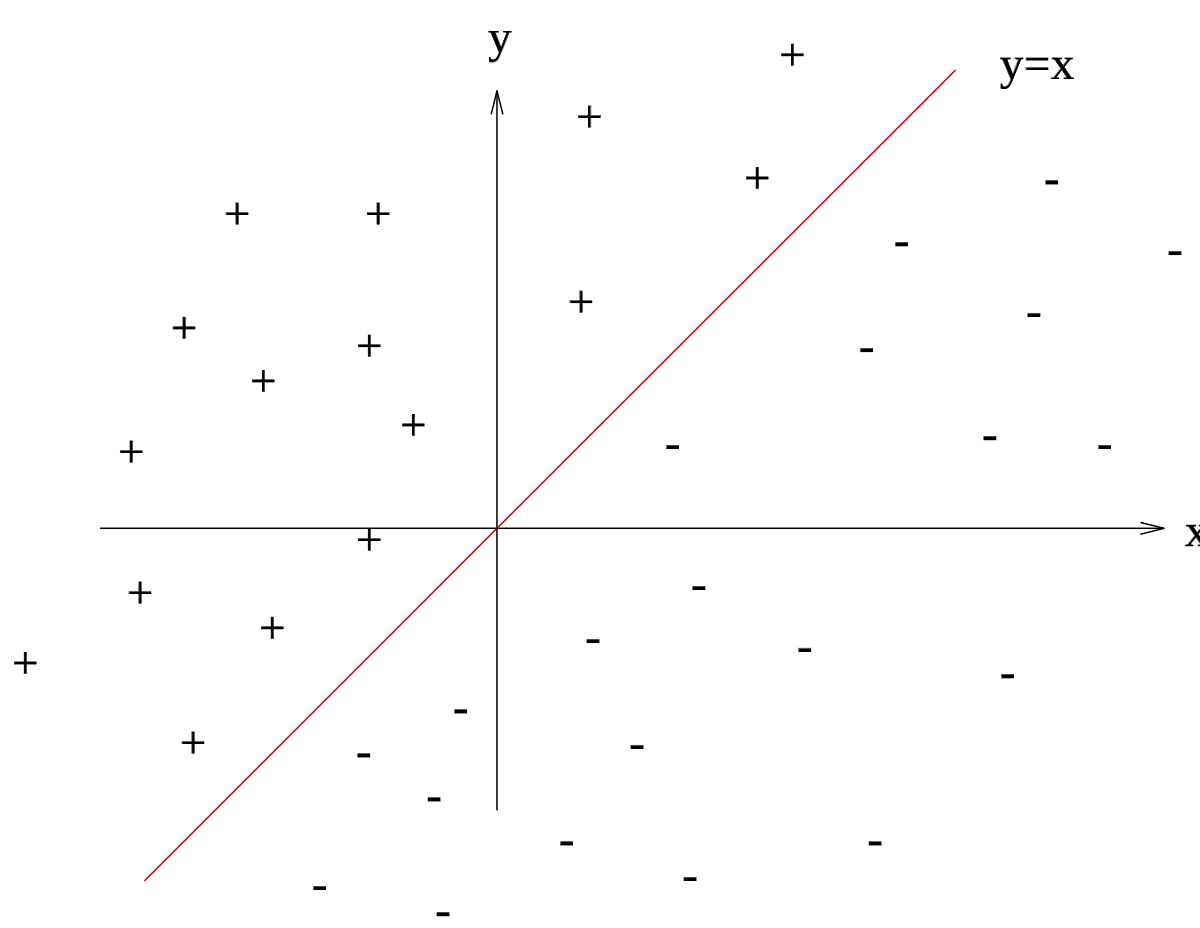
Exemple d'un problème de discrimination à deux classes, avec une séparatrice linéaire : la droite d'équation y=x. Le problème est linéairement séparable. | 
Exemple d'un problème de discrimination à deux classes, avec une séparatrice non-linéaire : le cercle unité. Le problème n'est pas linéairement séparable. |
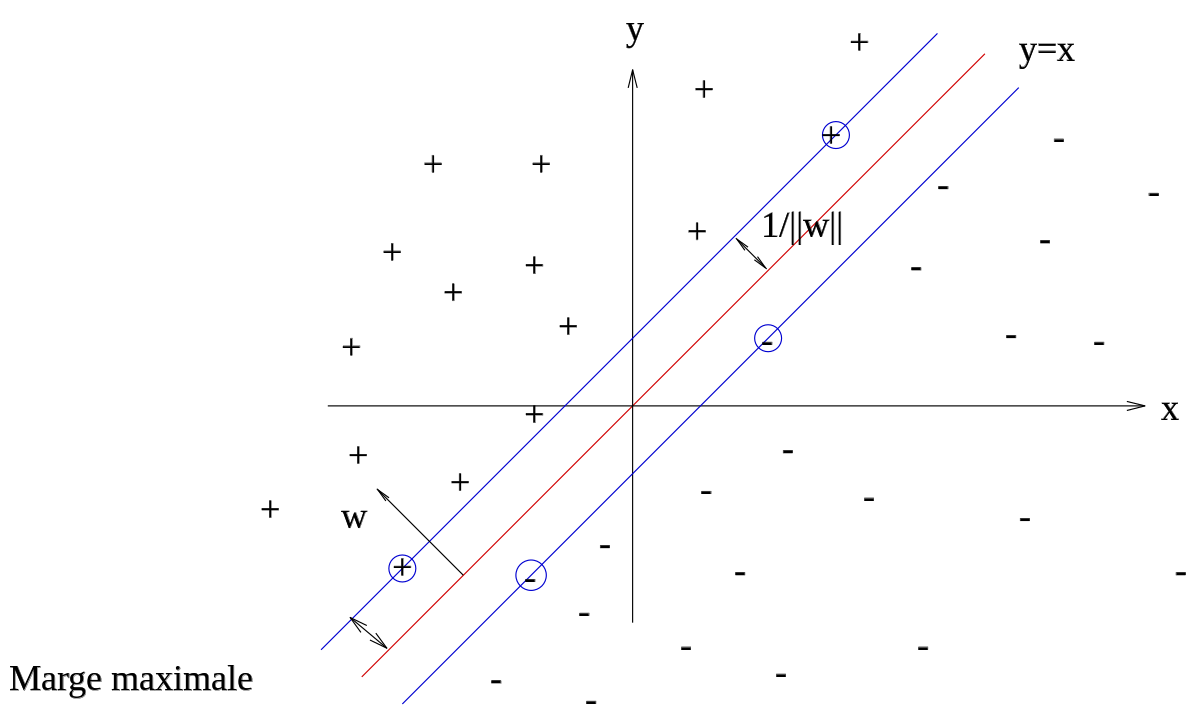
Marge maximale
On se place désormais dans le cas où le problème est linéairement séparable. Même dans ce cas simple, le choix de l'hyperplan séparateur n'est pas évident. Il existe en effet une infinité d'hyperplans séparateurs, dont les performances en apprentissage sont identiques (le risque empirique est le même), mais dont les performances en généralisation peuvent être très différentes. Pour résoudre ce problème, il a été montré, qu'il existe un unique hyperplan optimal, défini comme l'hyperplan qui maximise la marge entre les échantillons et l'hyperplan séparateur.
Il existe des raisons théoriques à ce choix. Vapnik a montré que la capacité des classes d'hyperplans séparateurs diminue lorsque leur marge augmente.
La marge est la distance entre l'hyperplan et les échantillons les plus proches. Ces derniers sont appelés vecteurs supports. L'hyperplan qui maximise la marge est donné par :
Il s'agit donc de trouver w et w0 remplissant ces conditions, afin de déterminer l'équation de l'hyperplan séparateur :
- h(x) = wTx + w0 = 0
Recherche de l'hyperplan optimal
Formulation primale
La marge est la plus petite distance entre les échantillons d'apprentissage et l'hyperplan séparateur qui satisfasse la condition de séparabilité (à savoir
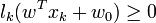
-
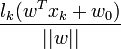
L'hyperplan séparateur (w,w0) de marge maximale est donc donné par:
Afin de faciliter l'optimisation, on choisit de normaliser w et w0, de telle manière que les échantillons à la marge (
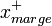
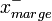
D'où pour tous les échantillons,
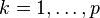
Cette normalisation est parfois appelée la forme canonique de l'hyperplan, ou hyperplan canonique.
Avec cette mise à l'échelle, la marge vaut désormais
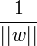
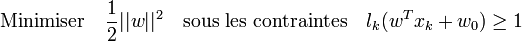
Ceci peut se résoudre par la méthode classique des Multiplicateur de Lagrange, où le lagrangien est donné par :
Le lagrangien doit être minimisé par rapport à w et w0, et maximisé par rapport à α.
Formulation duale
En annulant les dérivées partielles du lagrangien, selon les conditions de Kuhn-Tucker, on obtient :
En réinjectant ces valeurs dans l'équation (1), on obtient la formulation duale :
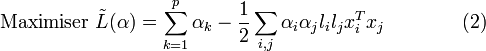
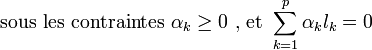
Ce qui donne les multiplicateurs de Lagrange optimaux
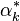
Afin d'obtenir l'hyperplan solution, on remplace w par sa valeur optimale w*, dans l'équation de l'hyperplan h(x) , ce qui donne :
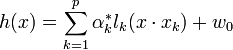
Conséquences
- Il y a trois remarques intéressantes à faire à propos de ce résultat. La première découle de l'une des conditions de Kuhn-Tucker, qui donne :
d'où
-
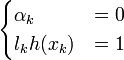
Les seuls points pour lesquels les contraintes du lagrangien sont actives sont donc les points tels que lkh(xk) = 1, qui sont les points situés sur les hyperplans de marges maximales. En d'autres termes, seuls les vecteurs supports participent à la définition de l'hyperplan optimal.
- La deuxième remarque découle de la première. Seul un sous-ensemble restreint de points est nécessaire pour le calcul de la solution, les autres échantillons ne participant pas du tout à sa définition. Ceci est donc efficace au niveau de la complexité. D'autre part, le changement ou l'agrandissement de l'ensemble d'apprentissage a moins d'influence que dans un modèle de mélanges gaussiens par exemple, où tous les points participent à la solution. En particulier, le fait d'ajouter des échantillons à l'ensemble d'apprentissage qui ne sont pas des vecteurs supports n'a aucune influence sur la solution finale.
- La dernière remarque est que l'hyperplan solution ne dépend que du produit scalaire entre le vecteur d'entrée et les vecteurs supports. Cette remarque est l'origine de la deuxième innovation majeure des SVM: le passage par un espace de redescription grâce à une fonction noyau.
Cas non séparable : Kernel trick
Principe

La notion de marge maximale et la procédure de recherche de l'hyperplan séparateur telles que présentées pour l'instant ne permettent de résoudre que des problèmes de discrimination linéairement séparables. C'est une limitation sévère qui condamne à ne pouvoir résoudre que des problèmes jouets, ou très particuliers. Afin de remédier au problème de l'absence de séparateur linéaire, l'idée des SVM est de reconsidérer le problème dans un espace de dimension supérieure, éventuellement de dimension infinie. Dans ce nouvel espace, il est alors probable qu'il existe une séparatrice linéaire.
Plus formellement, on applique aux vecteurs d'entrée x une transformation non-linéaire φ. L'espace d'arrivée φ(X) est appelé espace de redescription. Dans cet espace, on cherche alors l'hyperplan
- h(x) = wTφ(x) + w0
qui vérifie
- lkh(xk) > 0 , pour tous les points xk de l'ensemble d'apprentissage, c'est-à-dire l'hyperplan séparateur dans l'espace de redescription.
En utilisant la même procédure que dans le cas sans transformation, on aboutit au problème d'optimisation suivant :
Le problème de cette formulation est qu'elle implique un produit scalaire entre vecteurs dans l'espace de redescription, de dimension élevée, ce qui est couteux en termes de calculs. Pour résoudre ce problème, on utilise une astuce connue sous le nom de Kernel trick, qui consiste à utiliser une fonction noyau, qui vérifie :
d'où l'expression de l'hyperplan séparateur en fonction de la fonction noyau:
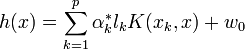
L'intérêt de la fonction noyau est double :
- Le calcul se fait dans l'espace d'origine, ceci est beaucoup moins coûteux qu'un produit scalaire en grande dimension.
- La transformation φ n'a pas besoin d'être connue explicitement, seule la fonction noyau intervient dans les calculs. On peut donc envisager des transformations complexes, et même des espaces de redescription de dimension infinie.
Choix de la fonction noyau
En pratique, on ne connait pas la transformation φ, on construit plutôt directement une fonction noyau. celle-ci doit respecter certaines conditions, elle doit correspondre à un produit scalaire dans un espace de grande dimension. Le théorème de Mercer explicite les conditions que K doit satisfaire pour être une fonction noyau : elle doit être symétrique, semi-définie positive.
L'exemple le plus simple de fonction noyau est le noyau linéaire :
On se ramène donc au cas d'un classifieur linéaire, sans changement d'espace. L'approche par Kernel trick généralise ainsi l'approche linéaire. Le noyau linéaire est parfois employé pour évaluer la difficulté d'un problème.
Des noyaux usuels employés avec les SVM sont:
- le noyau polynomial
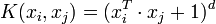
- le noyau gaussien
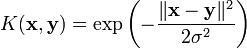
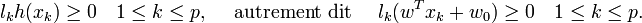

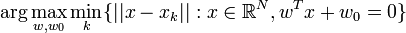
![\arg \max_{w,w_0} \left \{ \frac{1}{||w||} \min_k \left [ l_k(w^Tx_k+w_0) \right ] \right \}](https://static.techno-science.net/illustration/Definitions/autres/c/ceae17185779e88122e69261dabaa722_7eb66bf26d97b69b84695390813eef6d.png)
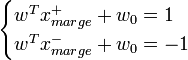
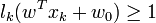
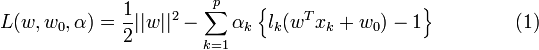
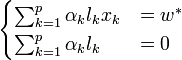
![\alpha_k [ l_k h(x_k)-1 ] = 0 \quad 1 \le k \le p.](https://static.techno-science.net/illustration/Definitions/autres/2/2f3e83931bdf6f835ba79bcc98c0b9e6_36ba122eeee9198de2a597dd56237ceb.png)