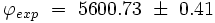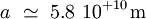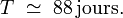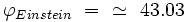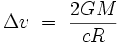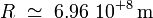Tests expérimentaux de la relativité générale - Définition

Introduction

La relativité générale a la réputation d'être une théorie fortement mathématique, impossible à relier à des résultats expérimentaux. C'est une erreur, car si ses postulats ne sont pas testables, elle prédit des effets observables de déviations par rapport aux théories physiques qui ont précédé.

Cette page expose donc les tests expérimentaux de la relativité générale.

Les tests historiques

Ces trois tests classiques de la relativité générale ont été proposés par Einstein lui-même.

Avance du périhélie de Mercure

Le 18 novembre 1915, Einstein présente à l'Académie de Prusse un manuscrit dans lequel il résout une énigme vieille de plus de soixante ans : l'anomalie de l'avance du périhélie de Mercure.

Position du problème

Selon la théorie de Newton, le problème de Kepler à deux corps {Soleil, Mercure} isolés du reste de l'Univers admet une solution exacte : la planète Mercure possède une orbite elliptique fixe dont le Soleil est un foyer.

Malheureusement, dans le système solaire, les deux corps {Soleil, Mercure} ne forment pas un système isolé, car ils sont soumis à l'attraction gravitationnelle des sept autres planètes. Les masses de toutes les planètes étant très petites devant la masse du Soleil, la solution de Képler peut être prise comme base pour une théorie des perturbations. En utilisant les équations de Newton, il est alors possible de démontrer que la trajectoire elliptique présente une précession lente : tout se passe comme si l'ellipse tournait lentement autour du Soleil, comme le montre la figure ci-contre (de façon très exagérée), le périhélie passant de la position rouge à la position bleue après une période de révolution. Cette rotation est caractérisée par l'angle dont le grand-axe de l'ellipse tourne d'une révolution à la suivante.

Dès le 12 septembre 1859, l'astronome Urbain Le Verrier présentait à l'Académie des sciences de Paris une note dans laquelle il montrait que lorsqu'on prenait en compte l'influence des autres planètes, on obtenait une valeur théorique pour l'avance du périhélie en désaccord avec la valeur expérimentale (en secondes d'arc par siècle) :

L'écart calculé par Le Verrier était d'environ 38 secondes d'arc par siècle. Des calculs plus précis faits par Newcomb en 1882, prenant également en compte le léger aplatissement du Soleil dû à sa rotation propre, donnent en fait la valeur théorique (en secondes d'arc par siècle) suivante :

soit un écart inexpliqué entre le résultat expérimental et la prédiction Newtonienne de :

Solution d'Einstein

En relativité générale, le problème à deux corps n'est pas exactement soluble ; seul le « problème à un corps » l'est. Dans son manuscrit de la fin 1915, Einstein commence par calculer le champ de gravitation à symétrie sphérique crée par un astre de masse M lorsqu'on se place loin du centre de l'astre, le champ étant alors de faible intensité. Einstein explore ensuite le problème du mouvement d'une « particule test » de masse dans ce champ faible. Il démontre en particulier que, pour une planète quelconque dans le champ de gravitation du Soleil, l'orbite Keplerienne subit bien une précession d'une quantité égale à:

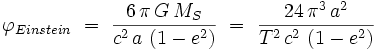
où a est le demi-grand axe de l'ellipse, e son excentricité, G la constante de gravitation universelle, M_S la masse du Soleil, et T la période de révolution sur l'ellipse. La démonstration complète de cette formule est présentée sur le site de Christian Magnan.

La planète Mercure étant la plus proche du Soleil, elle possède la plus petite valeur de a parmi toutes les planètes, et est donc la plus sensible à cette effet de précession. Ses valeurs numériques sont en effet:

• 

• 

• 

L'application numérique donne 0.1038 secondes d'arc par révolution. Mercure accomplissant 415 révolutions par siècle, on obtient en secondes d'arc par siècle :

Pour obtenir la prédiction théorique de la relativité générale, il reste à rajouter à cette valeur l'influence perturbatrice totale des autres planètes. On peut montrer qu'il est possible de la prendre en première approximation égale à la valeur calculée par la théorie de Newton, d'où :

On en déduit que l'écart entre la valeur expérimentale et la prédiction théorique de la relativité générale est nul à la précision des mesures près ; il vaut en effet (en secondes d'arc par siècle) :

Ce fut le premier grand succès de la relativité générale.

Courbure des rayons lumineux

Dans le même manuscrit daté du 18 novembre 1915, Einstein propose de tester la déviation d'un rayon lumineux dans le champ de gravitation d'un astre massif comme le Soleil. Cette prédiction du savant allemand sera confirmée en 1919, donc au sortir de la première guerre mondiale, par les résultats de deux expériences dirigées par l'astronome britannique Eddington.

Prédiction Newtonienne (calcul heuristique)

Soit un astre fixe de masse M et de rayon R situé à l'origine des coordonnées. Si le photon est de masse nulle, il ne subit aucune interaction gravitationnelle de l'astre dans la théorie de Newton et la question est sans objet.

Supposons donc que l'on attribue une masse au photon, afin que celui-ci soit influençable par la force de gravitation de Newton crée par l'astre. On imagine alors l'expérience de diffusion très simplifiée suivante, décomposable en trois phases successives :

1. Le photon est initialement libre : il ne subit aucune influence gravitationnelle. Il se déplace d'un mouvement rectiligne uniforme à la vitesse c en direction de l'astre sous incidence rasante.
2. Au voisinage de l'astre, le photon de vitesse c subit la force de Newton constante : F = GMm / R² pendant une durée :Δt = 2R / c, force qui fait varier son vecteur vitesse d'une quantité :
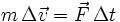
3. Le photon est de nouveau libre : il ne subit plus aucune influence gravitationnelle. Il se déplace en s'éloignant de l'astre d'un mouvement rectiligne uniforme à la vitesse c.

Il vient en rassemblant les morceaux du puzzle :

On en déduit que la variation de vitesse :

est indépendante de la valeur exacte de la masse m. De plus, sachant que les valeurs des vitesses initiales et finales sont égales à : v_i = v_f = c, la figure suivante :

permet de trouver la déviation angulaire :

Cette déviation étant très petite, on approxime par : , d'où la prédiction Newtonienne :

NB Le résultat du calcul rigoureux (« déviation Rutherford ») est exactement le même que celui obtenu par ce calcul heuristique très simplifié.

Pour le Soleil, on a les valeurs numériques suivantes :

• 

• 

d'où la prédiction Newtonienne en secondes d'arc :

Prédiction de la relativité générale

La relativité générale d'Einstein prédit une déviation deux fois plus grande que celle obtenue par les équations de Newton :

Résultats expérimentaux d'Eddington (1919)

Les expériences de 1919 consistent à observer le déplacement apparent d'étoiles voisines du Soleil sur le fond du ciel, déplacement mesuré par rapport à leur position habituelle lorsqu'elles ne se trouvent pas en incidence rasante.

La mesure en incidence rasante ne peut se faire que lors d'une éclipse de Soleil, seule possibilité de voir ces étoiles alors voisines du Soleil sur le fond du ciel. La difficulté de l'expérience vient du fait que les éclipses possèdent une durée relativement courte : les mesures doivent être faites rapidement, ce qui gêne la recherche de précision.

Les résultats expérimentaux publiés par Arthur Eddington et ses collaborateurs sont :

• Expérience de Sobral (Brésil) :
• Expérience de Principe (golfe de Guinée) :

La valeur donnée pour Sobral est celle de la lunette de secours. Pour la lunette principale de Sobral, la valeur mesurée est de 0,93, mais Eddington et ses collaborateurs ont conclu qu'il y avait eu des erreurs de manipulation, et donc la marge d'erreur ne peut être évaluée.

Validité des résultats

Les résultats d'Eddington confortent parfaitement les prédictions de la relativité générale, puisque les prédictions de celle-ci se trouvent toutes dans l'intervalle de confiance, tandis que les prédictions suivant la théorie de Newton sont en dehors.

Cependant, des critiques plus récentes affirment que la précision des mesures a été surestimée par Eddington. Avec des évaluations plus pessimistes, la marge d'erreur est du même ordre de grandeur que le phénomène à mesurer, et donc l'expérience ne permettait pas de rejeter la théorie de Newton.

Aujourd'hui, les avis sur la rigueur d'Eddington sont très partagés. Pour Jean-Marc Bonnet Bidaud, la sélection des mesures valables par Eddington relève du trucage, guidé par une véritable volonté de prouver à tout prix qu'Einstein avait raison. Pour Jean Eisenstaedt, dans Einstein et la relativité générale, au contraire, Eddington a agi avec une parfaite rigueur dans sa sélection des mesures les moins entachées d'erreur (puisque la relativité générale a bien été confirmée, il est légitime de dire aujourd'hui que la valeur de 0,93 devait bien être erronée, et les autres justes). Stephen Hawking, dans Une Brève histoire du temps, est plus mesuré : pour lui, les valeurs trouvées par Eddington malgré tous les facteurs d'erreur possible relèvent de l'effet expérimentateur, la tendance inévitable à lire dans les observations le résultat que l'on cherche alors qu'il est en fait indéterminé.

Répercussions de l'expérience

Les mesures annoncées par Eddington ont fait les gros titres de la presse de l'époque et ont contribué à faire accéder Einstein à la notoriété dans le grand public.

Cependant, les scientifiques sont plus hésitants. La Société astronomique royale britannique accueille les résultats avec prudence. Trop complexe pour des prédictions d'effets peu visibles, la relativité générale ne séduit la majorité des astrophysiciens que 40 ans plus tard (voir Âge d'or de la relativité générale). C'est un des facteurs expliquant qu'elle n'ai pas valu de prix Nobel à Einstein.

Sur le plan politique, la mobilisation des expérimentateurs britanniques pour vérifier la théorie d'un physicien allemand (même si Einstein était en fait helvético-allemand à l'époque) est vue comme un symbole fort de réconciliation après la Première Guerre mondiale.

Décalage vers le rouge