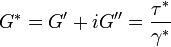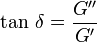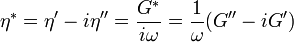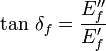Viscoanalyseur - Définition

Quelques propriétés mécaniques étudiées en DMA

Les propriétés des matériaux viscoélastiques dépendent du temps, de la température et de la vitesse de déformation (strain rate).

Les diverses propriétés correspondant aux modes de déformation en traction, en flexion ou en cisaillement (shear) sont représentées par des symboles portant l'indice t, f ou s, respectivement ; par exemple M_f est un module en flexion.

Pour l'essai de traction-compression uniaxiale, la mesure de la rigidité et le calcul de l'angle de phase permettent, connaissant uniquement les dimensions de l'éprouvette, de calculer les propriétés viscoélastiques δ, tan δ, E', E'' et E. Leur description ainsi que celle de la température de transition vitreuse Tg sont données ci-dessous.

Module de conservation E'

Le module de conservation en traction est calculé selon :

(en Pa).

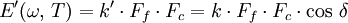
Le symbole représente l'angle de phase en traction (exprimé en pratique en degré) du matériau viscoélastique. Cet angle correspond au déphasage entre les signaux de déplacement et de force. Il est indépendant de la forme de l'échantillon. L'angle de phase (ou de perte) est le reflet de l'énergie dissipée (perdue) par le frottement des chaînes macromoléculaires.

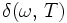
Le module de conservation E' représente la rigidité et la composante élastique du matériau. Il exprime la capacité du corps à stocker l'énergie mécanique de la sollicitation et à la restituer intégralement sous forme de déformation élastique (notion de réversibilité).

Si le matériau se comporte comme un solide élastique, les modules E' et E sont équivalents.

Module de perte E''

Il représente la composante visqueuse du matériau. La viscosité traduit sa capacité à dissiper l'énergie mécanique (irréversiblement perdue sous forme de chaleur). Ce phénomène est associé à la friction des chaînes de molécules et à leur écoulement. Le module de perte en traction a pour expression :

(en Pa).

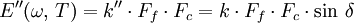
Module de Young complexe E*

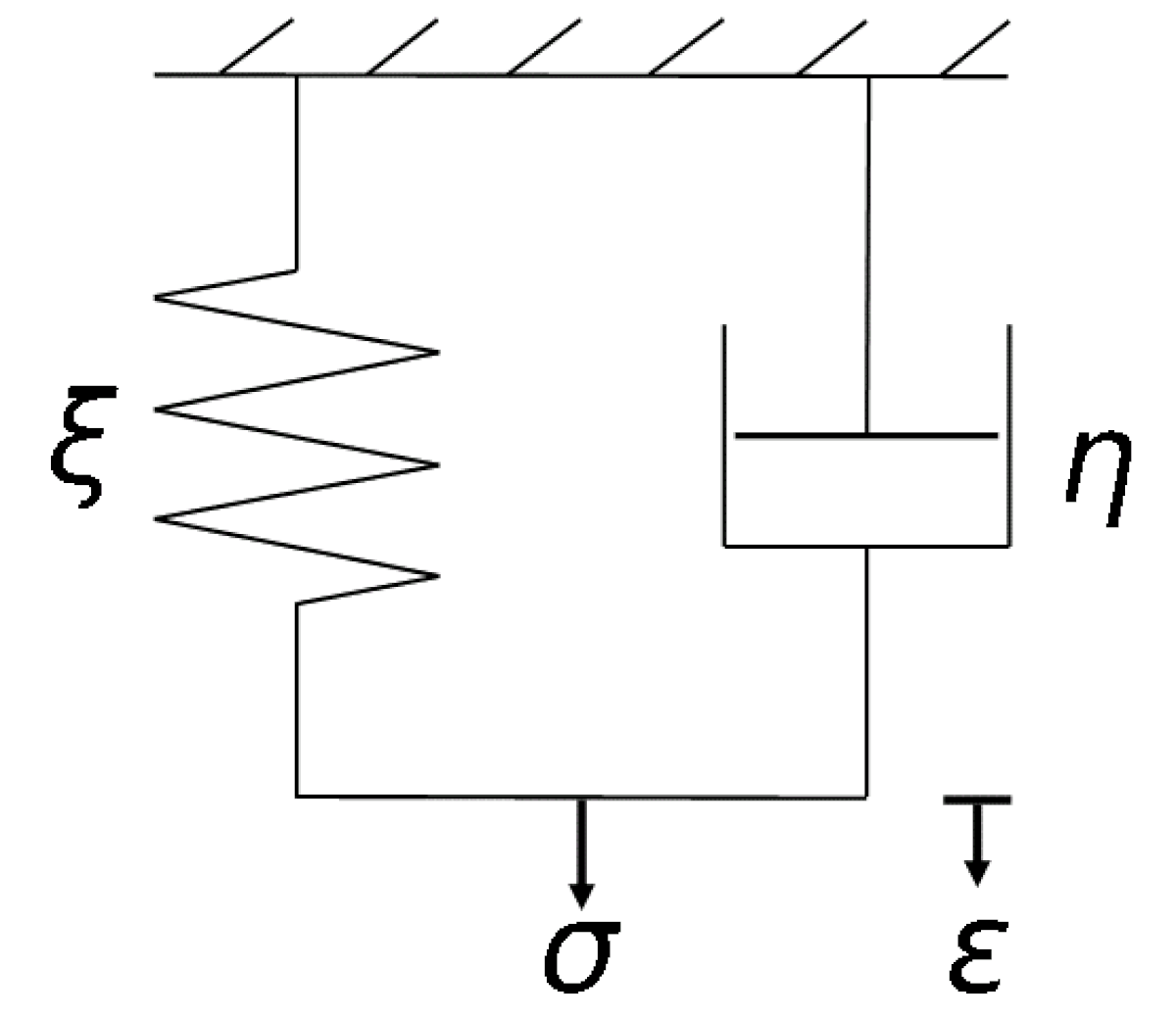
Modèle rhéologique

Par analogie avec la mécanique, un système comprenant un ressort idéal (de constante ) et un amortisseur idéal (de constante ) disposés en parallèle peut être utilisé pour modéliser le comportement viscoélastique d'un matériau. Ce système élémentaire est le modèle de Kelvin-Voigt. Sa réponse à l'excitation est régie par l'équation différentielle :

.

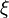
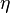
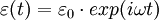
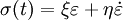
Le ressort représente la composante énergique ou élastique de la réponse du modèle ; tandis que l'amortisseur (constitué d'un piston se mouvant dans un cylindre rempli d'un liquide visqueux) représente la composante visqueuse de la réponse.
Les constantes caractéristiques et font respectivement référence au module d'élasticité et à la viscosité du matériau. L'équation peut être appliquée à la contrainte de cisaillement, , ou bien à la contrainte normale, σ, d'un matériau.

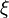
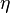
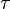
Un tel modèle présente un temps caractéristique relié aux constantes selon :

(en s).

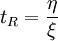
Il est désigné par temps de réponse du modèle ou temps de relaxation.

Le temps de relaxation d'un polymère est lié à la masse molaire, à la distribution des masses molaires et à la ramification.

Le module dynamique peut être exprimé sous forme complexe selon :

.

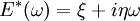
Les composantes réelle et imaginaire de ce module sont respectivement :

.

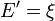
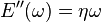
Le modèle de Voigt ne prédit pas de manière satisfaisante la relaxation de contrainte.

Le modèle rhéologique de Maxwell comprend un ressort et un amortisseur disposés en série.

Les matériaux ont des comportements bien plus complexes que ces deux modèles. Il existe d'autres modèles viscoélastiques plus performants, mais de complexité mathématique supérieure.

Théorie

En fait, les deux constantes de proportionnalité et précédemment décrites varient avec la fréquence, ce qui limite l'efficacité d'un modèle aussi simple. Une approche plus générale consiste à représenter le module complexe selon :

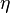
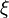
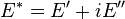
où E* est la somme vectorielle d'une composante élastique (en phase avec la contrainte) E' et d'une composante amortissante visqueuse (en quadrature de phase) E''.

Le module d'élasticité dynamique E* est une grandeur complexe car un amortissement est présent, en effet :

.

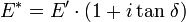
Le module E* représente la relation entre la contrainte et la déformation dynamiques, selon :

.

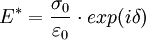
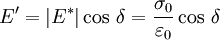
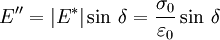
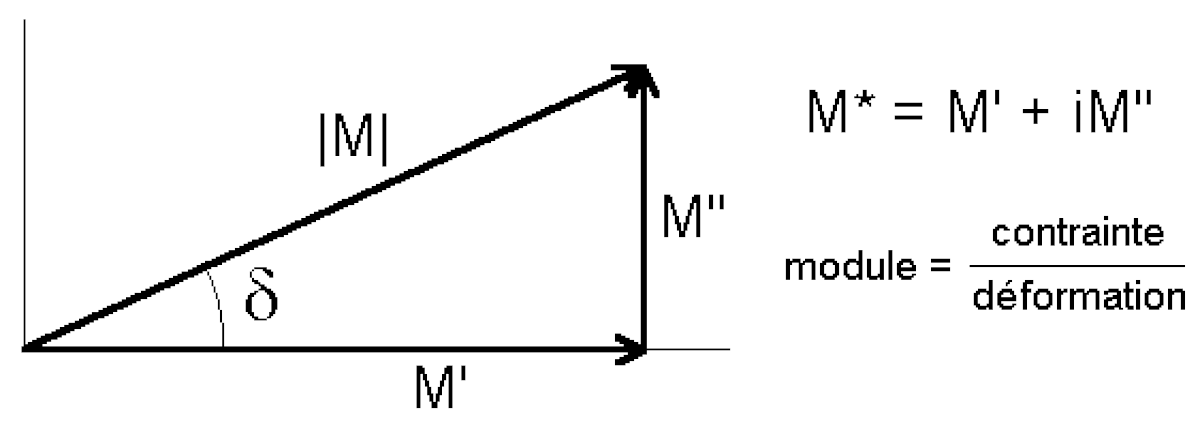
Grandeur |M| du module complexe M*

La grandeur réelle |M| est égale au module (au sens mathématique) du nombre complexe M* (E* ou G*) :

(en Pa).

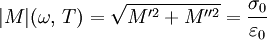
Annexe : notes sur les propriétés structurales

• le module (ou la rigidité) traduit la résistance d'un échantillon de matériau à un type de déformation mécanique (dans la limite des faibles déformations) ;
• en pratique, les modules sont généralement exprimés en MPa ou en GPa ;
• pour le comportement viscoélastique linéaire, l'inverse du module complexe M* est la complaisance complexe C* ;
• au cours d'une déformation plastique, le module de conservation d'un polymère diminue (en général) si l'amplitude de la déformation augmente ;
• hors cas de réticulation, de gélification ou d'évaporation en cours de test, le module M' diminue si la température augmente. La diminution peut être très importante dans la zone viscoélastique (voir § 9.1) ;
• le module M' augmente toujours avec la fréquence d'excitation. L'augmentation peut être importante si le matériau se trouve dans la zone viscoélastique (voir le graphique § 10). L'influence de la fréquence sur M' est moindre que celle de la température : plusieurs décades de fréquence entraînent la même variation que quelques degrés de température. Cet important phénomène de viscoélasticité est mis en évidence en caractérisation de matériaux viscoélastiques.

L'effet de la température sur les propriétés viscoélastiques d'un polymère est inverse à celui de la fréquence. Une augmentation de température d'une certaine valeur conduit aux mêmes changements de ses propriétés qu'une diminution appropriée de fréquence (et inversement). Si la propriété envisagée est le module, la relation s'écrit, pour un échantillon homogène, isotrope et amorphe :

.

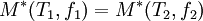
Ces phénomènes découlent du principe d'équivalence température-temps, sachant qu'une fréquence est l'inverse d'un temps.

Ce principe d'équivalence est utilisé pour transposer réversiblement les propriétés d'un matériau amorphe du domaine thermique au domaine fréquentiel. Le logiciel de l'appareil utilise ainsi ce principe pour le calcul de courbes maîtresses dynamiques, afin d'estimer les propriétés viscoélastiques du corps au-delà de la plage de fréquence de l'appareil (gamme du mHz au GHz accessible).

Facteur d'amortissement ou de perte tan δ

Définition

Le facteur d'amortissement est une mesure du rapport de l'énergie dissipée par amortissement à l'énergie élastique conservée puis restituée durant un cycle de déformation sinusoïdale.

Le facteur de perte (loss factor) en traction est égal à :

(sans unité ou exprimé en %).

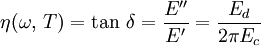
Il mesure l'amortissement (aussi appelé « friction interne ») durant la déformation dynamique, soit la capacité du corps viscoélastique à dissiper l'énergie mécanique en chaleur. Plus l'angle de phase est élevé, plus l'amortissement des vibrations (vibration damping) est important.
Remarques :

• la connaissance du facteur de perte revêt un intérêt pratique considérable ;
• contrairement à la rigidité, le facteur d'amortissement est indépendant de la forme de l'échantillon ;
• à la différence de la rigidité (ou du module d'élasticité), l'amortissement ne peut en général être déduit de simples mesures statiques ;
• un autre mode d'oscillation, utilisé par une autre méthode de test, et basé sur des fréquences proches de la résonance, peut faire intervenir un taux d'amortissement (damping ratio). Le facteur d'amortissement est égal à deux fois le taux d'amortissement, soit :  ;
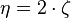
• la résilience est une propriété approximativement reliée au facteur de perte.

Échelle d'amortissement

Les matériaux caoutchouteux sont bien connus pour leur faculté d'amortissement de vibrations, participant à la réduction du bruit.
Exemple : pour un caoutchouc de haute masse molaire partiellement vulcanisé, on relève à 40 Hz : Tg = 60 °C, = 1 (valeur élevée) à 60 °C et E' = 200 MPa (à 60 °C).
À l'opposé, le facteur d'amortissement des métaux est très faible : au plus 10^-3 pour l'acier.

Classement approximatif de quelques matériaux courants selon leur facteur de perte à la température ambiante et dans le domaine des audiofréquences.

Facteur de perte	Matériau
100 et plus	Polymère ou élastomère approprié (exemple : caoutchouc butyle)
10-1	Caoutchouc naturel, PVC avec plastifiant, sable sec, asphalte, liège, matériau composite de structure sandwich (tricouche métal / polymère / métal)
10-2	Plexiglas, bois, béton, feutre, plâtre, brique
10-3	Acier, fer, plomb, cuivre, verre
10-4	Aluminium, magnésium

Il existe de nombreuses méthodes pour évaluer la performance des matériaux amortissants.

Cas d'un mode de déformation en cisaillement

Les propriétés relatives à une contrainte normale à une surface ont été décrites. De façon analogue, les propriétés en cisaillement d'un matériau viscoélastique peuvent être considérées. Les relations de base entre ces propriétés s'écrivent :

avec :

et , les modules respectifs de conservation et de perte en cisaillement

et , respectivement la contrainte et la déformation complexes en cisaillement

, la viscosité complexe, fréquemment utilisée pour décrire les liquides viscoélastiques

, la viscosité dynamique exprimée en pascal-seconde, proportionnelle à .

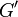
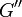
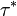
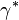
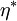
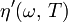
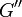
Le comportement des plastiques et des élastomères homogènes et isotropes est tel que :

• le module de cisaillement G est quasiment égal au tiers du module en traction E ;
• le facteur de perte en cisaillement est quasiment égal au facteur de perte en traction.

Cas d'un mode de déformation en flexion

À la différence de l'essai de traction, les mesures en flexion sont influencées préférentiellement par les propriétés des couches superficielles de l'éprouvette.

Les valeurs des propriétés produites par l'essai de traction et celles produites par l'essai de flexion sont comparables seulement en viscoélasticité linéaire, et pour des éprouvettes de structure homogène.

Le facteur de perte en flexion est donné par l'équation :

avec :

, l'angle de phase en flexion

et , les modules de conservation et de perte en flexion, respectivement.

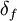
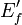
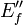
Exemple d'application : un échantillon de matériau composite est soumis à une flexion ; il sera possible d'étudier la variation du module d'élasticité en fonction de l'orientation des fibres ou des plis par rapport aux appuis.

Température de transition vitreuse Tg

L'analyseur DMA est l'appareil le plus sensible pour sa détermination.

De façon générale, le signal d'amortissement permet de définir très clairement la température de transition vitreuse.

La valeur de Tg est déterminée en traçant la courbe à isofréquence = f (T). La température à laquelle la valeur du facteur de perte est maximale est appelée température de transition vitreuse : Tg ou Tv.

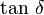
Remarques :

• la valeur de la température de transition vitreuse d'un polymère augmente avec la fréquence de la sollicitation mécanique ;
• le comportement viscoélastique d'un polymère, lié à sa phase amorphe, se révèle dans la zone de transition, au voisinage de sa Tg ;
• la valeur de Tg dépend de multiples facteurs physico-chimiques ;
• de très nombreuses propriétés physiques subissent une variation à Tg ;
• ainsi, de nombreuses techniques, dont la DSC, permettent sa mesure. L'Analyse Thermique DSC est complémentaire de l'Analyse Thermomécanique.

La connaissance de Tg présente, dans la pratique, un intérêt considérable car elle conditionne le domaine d'utilisation du matériau.

La température de transition vitreuse est la température maximale d'utilisation pour les thermoplastiques rigides et amorphes (leur Tg est supérieure à 100 °C ; leur température de mise en œuvre est voisine de leur Tg) mais elle est la température minimale d'utilisation des élastomères (leur Tg est inférieure à -40 °C).