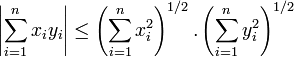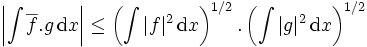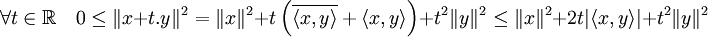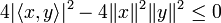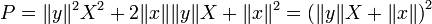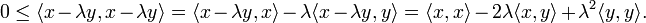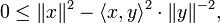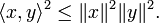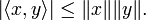Inégalité de Cauchy-Schwarz - Définition
En mathématiques, l'inégalité de Cauchy-Schwarz, aussi appelée inégalité de Schwarz, ou encore inégalité de Cauchy-Bunyakovski-Schwarz, se rencontre dans de nombreux domaines tels que l'algèbre linéaire avec les vecteurs, l'analyse avec les séries et en intégration avec les intégrales de produits.
L'inégalité s'énonce de la façon suivante :
- Pour tous x et y éléments d'un espace préhilbertien réel ou complexe
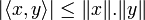
Les deux membres sont égaux si et seulement si x et y sont linéairement dépendants.
Conséquences
Une conséquence de l'inégalité de Cauchy-Schwarz est que le produit scalaire est une fonction continue.
Dans le cas de l'espace euclidien 
muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :
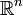
Dans le cas des fonctions à valeurs complexes de carré intégrable, l'inégalité de Cauchy-Schwarz s'écrit :
Ces deux dernières formulations sont généralisées par l'inégalité de Hölder.
Démonstration
Démontrons le résultat dans le cas d'un préhilbertien complexe.
Inégalité
Pour tout couple de vecteurs (x,y), par définition du produit scalaire hilbertien et de la norme associée:
On note que la dernière inégalité a un sens car 
est une quantité réelle (propriété élémentaire de la conjugaison). On l'a majorée par sa valeur absolue (module) et on lui a appliqué l'inégalité triangulaire dans 
.
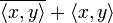
Ainsi, le polynôme à coefficients réels 
d'inconnue X, est positif sur 
d'après la relation précédente. Il ne peut donc pas avoir deux racines réelles distinctes. Ceci implique que son discriminant est négatif. On obtient:
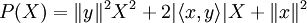
Ce qui entraîne bien l'inégalité annoncée.
Cas d'égalité
Si les vecteurs x et y sont liés, on peut sans perte de généralité supposer que 
. On en déduit immédiatement: 
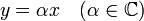
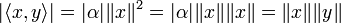
Réciproquement, supposons qu'on ait l'égalité 
Si y=0, les vecteurs sont liés. Si y
0, le polynôme ci-dessus s'écrit :
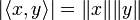
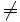
Il admet pour racine réelle double 
, d'où 
, puis x + t0y = 0. D'où le résultat.
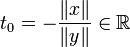
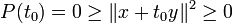
Cas réel
Dans le cas d'un espace réel la démonstration est analogue. On peut aussi proposer une preuve légèrement différente :
La preuve pour y = 0 est triviale, on considère donc 
. Pour 
on a :
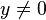
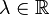
Prenons 
de sorte que :
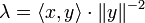
Ainsi
Puis
Cette preuve peut facilement être adaptée au cas complexe.
| Articles de mathématiques en rapport avec l'algèbre bilinéaire |
| Espace euclidien | Forme bilinéaire | Forme quadratique | Forme sesquilinéaire | Orthogonalité | Base orthonormale | Projection orthogonale | Inégalité de Cauchy-Schwarz | Inégalité de Minkowski | Matrice définie positive | Matrice semi-définie positive | Décomposition QR | Déterminant de Gram | Hermitien | Espace de Hilbert | Base de Hilbert | Théorème spectral | Théorème de Stampacchia | Théorème de Riesz | Théorème de Lax-Milgram | Théorème de représentation de Riesz |