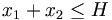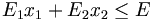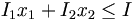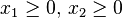Programmation linéaire - Définition

En mathématiques, les problèmes de programmation linéaire (PL) sont des problèmes d'optimisation où la fonction objectif et les contraintes sont toutes linéaires. Néanmoins, la plupart des résultats présentés ici sont également vrais si l'objectif est une fonction monotone croissante de chaque variable considérée. La programmation linéaire désigne également la manière de résoudre les problèmes de PL.

La programmation linéaire est un domaine central de l'optimisation, car les problèmes de PL sont les problèmes d'optimisation les plus faciles - toutes les contraintes y étant linéaires. Beaucoup de problèmes réels de recherche opérationnelle peuvent être exprimés comme un problème de PL. Pour cette raison un grand nombre d'algorithmes pour la résolution d'autres problèmes d'optimisation sont fondés sur la résolution de problèmes linéaires.

Le terme programmation linéaire suppose que les solutions à trouver doivent être représentées en variables réelles. S'il est nécessaire d'utiliser des variables discrètes dans la modélisation du problème, on parle alors de programmation linéaire en nombres entiers (PLNE). Il est important de savoir que ces derniers sont nettement plus difficiles à résoudre que les PL à variables continues.

Exemple

Considérons un agriculteur qui possède des terres, de superficie égale à H hectares, dans lesquelles il peut planter du blé et du maïs. L'agriculteur possède une quantité E d'engrais et I d'insecticide. Le blé nécessite une quantité E₁ d'engrais par hectare et I₁ d'insecticide par hectare. Les quantités correspondantes pour le maïs sont notées E₂ et I₂.

Soit P₁ le prix de vente du blé et P₂ celui du maïs. Si l'on note par x₁ et x₂ le nombre d'hectares à planter en blé et en maïs, alors le nombre optimal d'hectares à planter en blé et en maïs peut être exprimé comme un programme linéaire:

maximise	P1x1 + P2x2	(maximiser le revenu net)
sous contraintes		(borne sur le nombre total d'hectares)
		(borne sur la quantité d'engrais)
		(borne sur la quantité d'insecticide)
		(on ne peut pas planter un nombre négatif d'hectares)

Théorie

D'un point de vue géométrique, les contraintes linéaires forment un polyèdre convexe. Si la fonction objectif est elle aussi linéaire, tous les optima locaux sont également des optima globaux; cela reste vrai si elle est monotone croissante sur chaque variable considérée, le cas linéaire ne représentant qu'un cas particulier dont la propriété n'est d'ailleurs pas utilisée.

Il y a deux cas où il n'existe pas de solution optimale. Le premier est lorsque les contraintes se contredisent mutuellement (par exemple ). Dans un tel cas, le polytope est vide et il n'y a pas de solution optimale puisqu'il n'y a pas de solution du tout. Le PL est alors infaisable.

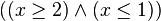
Le polyèdre peut également être non-borné dans la direction définie par la fonction objectif (par exemple x₁ + 3x₂ tel que , , ). Dans ce cas, il n'y a pas de solution optimale puisqu'il est possible de construire des solutions satisfaisant les contraintes avec des valeurs arbitrairement élevées (ou basses) de la fonction objectif.

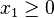
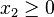
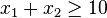
En dehors de ces deux cas (qui sont finalement rares dans les problèmes pratiques), l'optimum est toujours atteint à un sommet du polytope. Cependant, l'optimum n'est pas nécessairement unique: il est possible d'avoir un ensemble de solutions optimales correspondant à une arête ou à une face du polytope, voire au polytope en entier.

Dualité

Tous les programmes linéaires peuvent s'écrire sous la forme suivante:

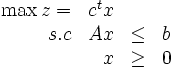
Où c et x sont des vecteurs de taille n, b un vecteur de taille m, et A une matrice de taille mXn. Si on désigne cette représentation sous le terme de forme primale, on désigne alors sous le terme de forme duale le problème suivant:

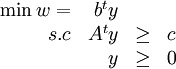
Où A, b et c sont les mêmes et y un vecteur de taille m. (Note: Les détails exacts des deux représentations varient beaucoup d'un ouvrage à l'autre)

Les deux problèmes sont très fortement liés. Si l'un d'entre eux possède une solution optimale, alors l'autre aussi. De plus, les deux solutions ont alors la même valeur (w*=z*). Si l'un d'entre eux est non-borné, l'autre ne possède pas de solution.

Outre son intérêt théorique, le problème dual possède de très intéressantes applications économiques. A chaque contrainte primale correspond une variable duale. La valeur de cette variable dans la solution optimale représente le coût marginal associé à la contrainte primale.

Algorithmes

L'algorithme du simplexe permet de résoudre les problèmes de PL en construisant tout d'abord une solution faisable qui est un sommet du polytope puis en se déplaçant selon les arêtes du polytope pour atteindre des sommets pour lesquels la valeur de l'objectif est de plus en plus grande, jusqu'à atteindre l'optimum. Bien que cet algorithme soit efficace en pratique et qu'il soit assuré de trouver l'optimum, son comportement dans le pire cas peut être mauvais. Il est ainsi possible de construire un PL pour lequel la méthode du simplexe requiert un nombre d'étapes exponentiel en la taille du problème. Ainsi, pendant plusieurs années, savoir si la PL était un problème NP-complet ou polynomial est resté une question ouverte.

Le premier algorithme polynomial pour la PL a été proposé par Leonid Khachiyan en 1979. Il est basé sur la méthode de l'ellipsoïde en optimisation non linéaire précédemment proposée par Naum Shor. Cette méthode est elle-même une généralisation de la méthode de l'ellipsoïde en optimisation convexe due à Arkadi Nemirovski (Prix John von Neumann 2003), et à D. Yudin.

Cependant, l'efficacité pratique de l'algorithme de Khachiyan est décevante: l'algorithme du simplexe est pratiquement toujours plus performant. En revanche, ce résultat a encouragé la recherche dans les méthodes de point intérieur. Par opposition à l'algorithme du simplexe qui considère uniquement la frontière du polytope définie par les contraintes, les méthodes de point intérieur évoluent à l'intérieur du polytope.

En 1984, N. Karmarkar propose la méthode projective. C'est le premier algorithme efficace à la fois en théorie et en pratique. Sa complexité dans le pire cas est polynomiale et les expérimentations sur les problèmes pratiques montrent que la méthode peut raisonnablement être comparée à l'algorithme du simplexe. Depuis lors, plusieurs méthodes de point intérieur ont été proposées et étudiées. Une des méthodes les plus célèbres est la méthode prédictive/corrective qui fonctionne très bien en pratique même si son étude théorique est encore imparfaite.

Pour la résolution pratique de problèmes de PL ordinaires, il est actuellement commun de considérer comme équivalentes les (bons) codes basés sur les méthodes dérivées du simplexe ou du point intérieur. De plus, pour la résolution de problèmes de grande taille, une technique comme la génération de colonnes peut se révéler extrêmement efficace.

Les solveurs basés sur la PL sont de plus en plus utilisés pour l'optimisation de divers problèmes industriels tels que l'optimisation des flux de transports ou la planification de la production. Toutefois, les modèles de PL se révèlent insuffisants pour représenter de nombreux problèmes, la programmation linéaire en nombres entiers permet alors de modéliser un grand nombre de problèmes supplémentaires.

Programmation linéaire en nombres entiers

Un problème de programmation linéaire en nombres entiers (PLNE) est un programme linéaire, c'est-à-dire une fonction objectif linéaire à maximiser ou minimiser, sous des contraintes linéaires, dans lequel il y a la contrainte supplémentaire que les variables sont entières. On parle de programme linéaire mixte lorsque seul un sous-ensemble de variables doivent être entières et les autres réelles.

Il est facile de montrer que la PLNE est un problème NP-complet car de nombreux problèmes NP-complets peuvent être exprimés comme des PLNE. Bien entendu, les algorithmes décrits ci-dessus pour la PL ne résolvent pas les problèmes de PLNE. En revanche, la relaxation continue d'un PLNE (c'est le PLNE sans les contraintes d'intégrité) est un PL qui peut être résolu efficacement. Les algorithmes de résolution de PLNE, tels que les algorithmes par séparation et évaluation ou les algorithmes de génération de plans sécants, se basent très souvent sur cette relaxation continue.

Applications

La programmation linéaire est essentiellement appliquée pour résoudre des problèmes d'optimisation à moyen et long terme (problèmes stratégiques et tactiques, dans le vocabulaire de la recherche opérationnelle). Les domaines d'application de ces problèmes sont très nombreux aussi bien dans la nature des problèmes abordés (planification et contrôle de la production, distribution dans des réseaux) que dans les secteurs d'industrie: industrie manufacturière, énergie (pétrole, gaz, électricité, nucléaire), transports (aériens, routiers et ferroviaires), télécommunications, industrie forestière, finance.

Applications dans le pétrole

La technique de la programmation linéaire est couramment appliquée dans l'industrie pétrolière. C'est l'une des industries, si ce n'est la principale qui utilise quotidiennement la PL (programmation linéaire). Elle est l'outil qui permet au raffineur de faire la détermination optimale de production d'une raffinerie. Pour ce faire, le programme doit tenir compte d'un certain nombre de contraintes telles que :

• bruts disponibles, leurs rendements et les qualités des coupes,
• spécifications des produits à fabriquer,
• limitations de débouchés pour certains produits,
• capacités des unités,
• modes de réglages des installations,
• capacités de stockage disponibles.

La PL peut également être utilisée dans d'autres domaines du raffinage, par exemple :

• calculs de la composition optimale des mélanges de produits (carburants, gasoils, fuels) en tenant compte des spécifications.
• l'optimisation dans l'utilisation des installations,
• calculs de l'obtention du meilleur préchauffage des bruts et des charges,
• détermination du meilleur équilibre "vapeur-électricité" d'une raffinerie.

En dehors des raffineries, on peut utiliser la PL dans la recherche opérationnelle pour :

• bâtir des plans à long/moyen et court termes d'une compagnie pétrolière,
• optimiser le fonctionnement d'une flotte de tankers et la mise en place des produits.

Bibliographie

• Christelle Guéret, Christian Prins et Marc Sevaux : "Programmation Linéaire". Eyrolles, 2000. ISBN 2-212-09202-4, 365 pages.

• Eric Jacquet-Lagrèze. Programmation Linéaire - Modélisation et mise en œuvre informatique Collection : P.I.Q. Poche - Editeur : Economica