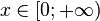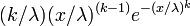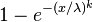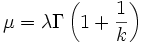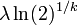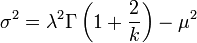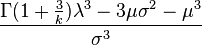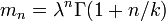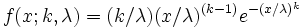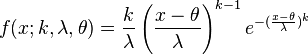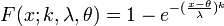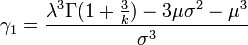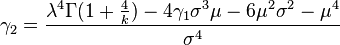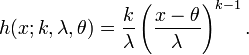Distribution de Weibull - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Weibull | |
|---|---|
| |
| |
| | |
| Paramètres |  échelle (réel) échelle (réel) forme (réel) forme (réel) |
| Support |
|
| Densité de probabilité (fonction de masse) |
|
| Fonction de répartition |
|
| Espérance |
|
| Médiane (centre) |
|
| Mode |
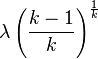
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) | voir texte |
| Entropie |
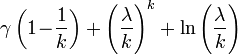
|
| Fonction génératrice des moments |
|
| modifier | |
En théorie des probabilités, la loi de Weibull, nommée d'après Waloddi Weibull, est une loi de probabilité continue.
Fonctions caractéristiques
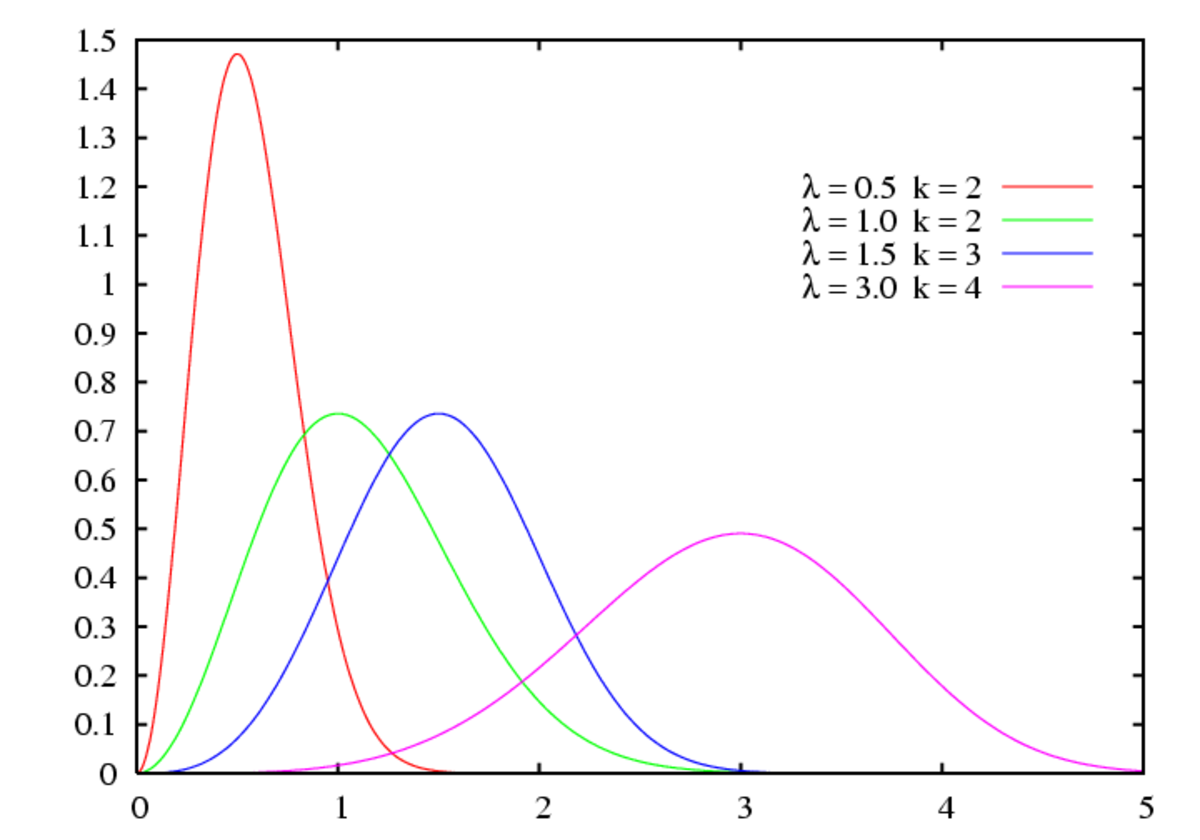
Avec deux paramètres sa densité de probabilité est :
où k > 0 est le paramètre de forme et λ > 0 le paramètre d'échelle de la distribution.
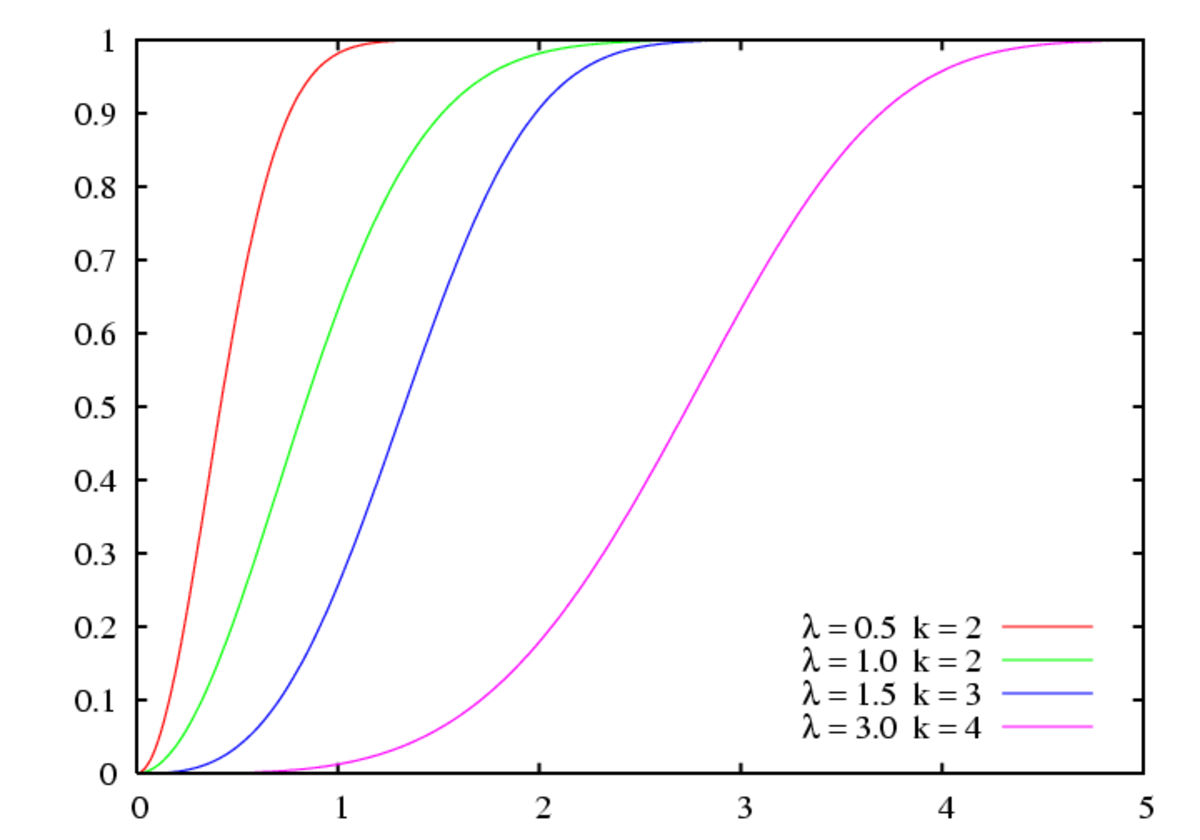
Sa fonction de répartition est définie par :
où, ici encore, x > 0.
Avec trois paramètres (généralisé) sa densité de probabilité est:
Pour x ≥ θ et f(x; k, λ, θ) = 0 pour x < θ, où k > 0 est le paramètre de forme, λ > 0 est le paramètre d'échelle et θ est le paramètre de localisation de la distribution.
Sa fonction de répartition pour la loi de Weibull 3-paramètres est définie par :
Pour x ≥ θ, et F(x; k, λ, θ) = 0 pour x < θ.
Le coefficient d'asymétrie (skewness) est donné par:
Le kurtosis est donné par:
Le taux de panne h est donné par :
Utilisation pratique
Généralités
L'expression loi de Weibull recouvre en fait toute une famille de lois, certaines d'entre elles apparaissant en physique comme conséquence de certaines hypothèses. C'est, en particulier, le cas de la loi exponentielle (k = 1) et de la loi de Rayleigh (k = 2) importantes en matière de processus stochastique.
Ces lois constituent surtout des approximations particulièrement utiles dans des techniques diverses alors qu'il serait très difficile et sans grand intérêt de justifier une forme particulière de loi. Une distribution à valeurs positives (ou, plus généralement mais moins fréquemment, à valeurs supérieures à une valeur donnée) a presque toujours la même allure. Elle part d'une fréquence d'apparition nulle, croît jusqu'à un maximum et décroît plus lentement. Il est alors possible de trouver dans la famille de Weibull une loi qui ne s'éloigne pas trop des données disponibles en calculant
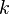

Application particulière
La distribution de Weibull est souvent utilisée dans le domaine de l'analyse de la durée de vie, grâce à sa flexibilité : comme dit précédemment, elle permet de représenter au moins approximativement une infinité de lois de probabilité.
Si le taux de panne diminue au cours du temps alors, k < 1. Si le taux de panne est constant dans le temps alors, k = 1. Si le taux de panne augmente avec le temps alors, k > 1. La compréhension du taux de panne peut fournir une indication au sujet de la cause des pannes.
- Un taux de panne décroissant relève d'une "mortalité infantile". Ainsi, les éléments défectueux tombent en panne rapidement, et le taux de panne diminue au cours du temps, quand les éléments fragiles sortent de la population.
- Un taux de panne constant suggère que les pannes sont liées à une cause stationnaire.
- Un taux de panne croissant suggère une "usure ou un problème de fiabilité" : les éléments ont de plus en plus de chances de tomber en panne quand le temps passe.
On dit que la courbe de taux de panne est en forme de baignoire. Selon l'appareil, baignoire sabot ou piscine. Les fabricants et distributeurs ont tout intérêt à bien maitriser ces informations par type de produits afin d'adapter :
- les durées de garantie (gratuites ou payantes)
- le planning d'entretien (voir MTBF)