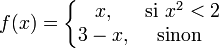Nombre réel - Définition
La liste des auteurs de cet article est disponible ici.
Aspect historique
Origine des nombres
Mise en place des fractions
Depuis l'Antiquité la représentation d'une grandeur mesurable — par exemple une longueur ou une durée — a répondu à un besoin. La première réponse fut la construction des fractions (quotient de deux entiers positifs). Cette solution, mise en place très tôt chez les Sumériens et les Égyptiens, est finalement performante. Elle permet d'approcher une longueur quelconque avec toute la précision souhaitée.
Correspondance avec des longueurs
La première formalisation construite en système que l'on connaisse est le fruit du travail d'Euclide au IIIe siècle av. J.-C. Sa construction, inscrite dans les Éléments d'Euclide, apporte deux grandes idées d'un apport majeur dans l'histoire des mathématiques.
- Les mathématiques sont formalisées avec des axiomes, des théorèmes et des démonstrations. On peut alors construire un système, avec des théorèmes dont les démonstrations s'appuient sur d'autres théorèmes. Les mathématiques sont classées en catégories, la géométrie et l'arithmétique en sont les deux plus grandes. Parler de construction prend alors tout son sens.
- Un pont est bâti entre les deux grandes catégories. Cette démarche, permettant d'utiliser des résultats d'une des branches des mathématiques pour éclairer une autre branche est des plus fécondes. Les nombres sont alors mis en correspondance avec des longueurs de segments.
Problèmes d'incomplétude
Irrationalité de la racine carrée de 2
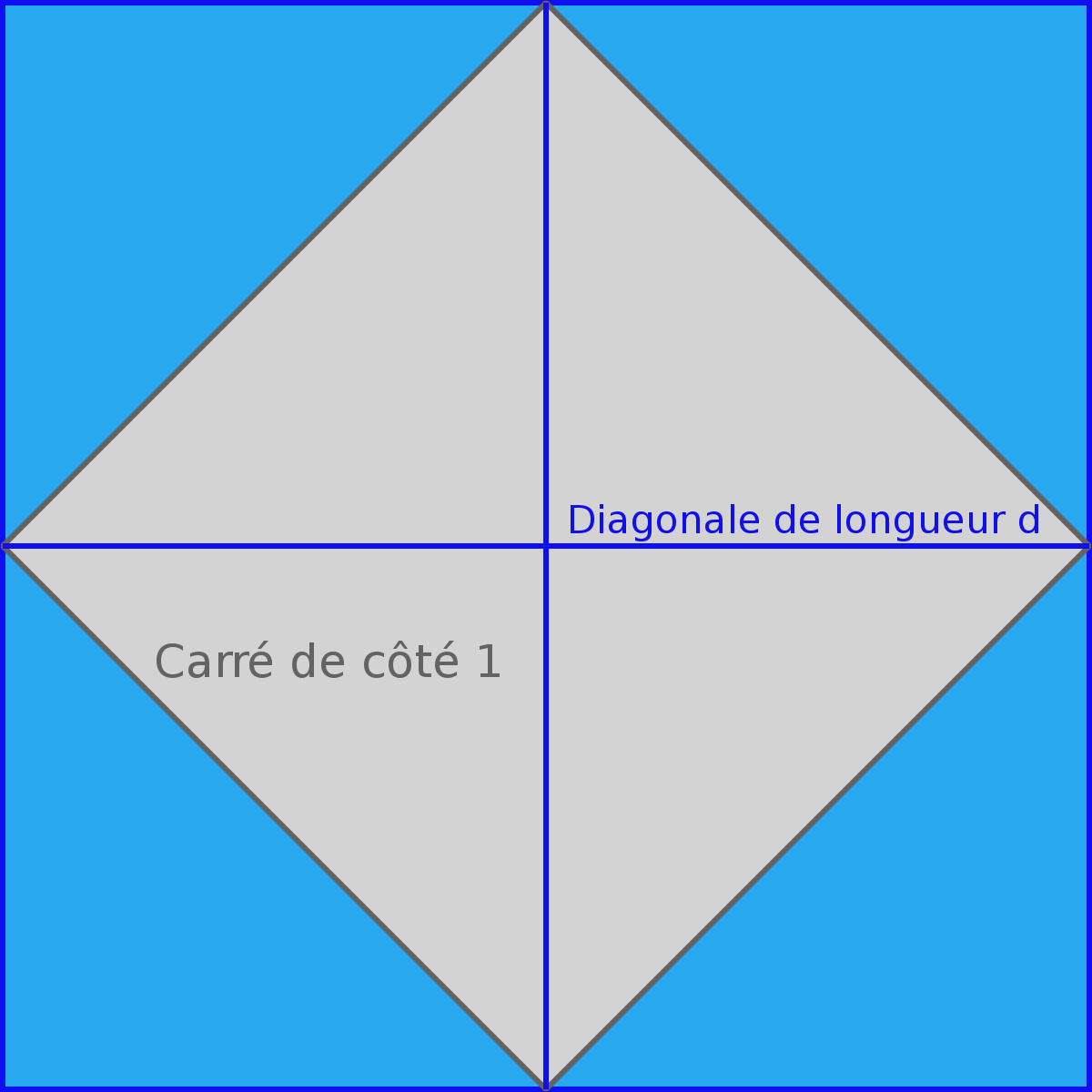
Supposons une longueur donnée choisie comme unité. Alors il existe une longueur dont le carré est égal à 2 fois l'unité. Un raisonnement géométrique, certainement déjà connu des babyloniens, montre qu'il est possible de construire un carré B de surface double de celle d'un carré initial A que l'on choisit de côté égal à 1. Si l'on note d la longueur du côté du carré B, qui est égale à la longueur de la diagonale du carré A, l'égalité d2 = 2 est alors vérifiée.
Probablement au Ve siècle av. JC, des mathématiciens grecs démontrent que les longueurs de la diagonale du carré et de son côté sont incommensurables : il n'existe pas de segment, aussi petit soit-il, qui permette de « mesurer » exactement ces deux grandeurs. Nous disons aujourd'hui que ce rapport de longueur, qui est la racine carrée de 2, est irrationnel, c'est-à-dire qu'il n'est pas égal à une fraction : si c'était une fraction m⁄n, en divisant la diagonale du carré en m parties égales et son côté en n parties égales on obtiendrait bien des segments tous de même longueurs.
Ceci met en évidence que les fractions ne peuvent suffire pour représenter les grandeurs mesurables.
Il existe une démonstration arithmétique simple de ce résultat, qui repose sur un argument de parité. Au IVe siècle av. JC Aristote y fait allusion dans un de ses écrits. On la trouve plus détaillée dans le livre X des éléments d'Euclide.
L'irrationalité de √2 se démontre par l'absurde. Supposons que √2 soit rationnel, c'est-à-dire qu'il existe deux entiers p et q (strictement positifs) tels que √2 = p⁄q. On peut supposer, quitte à simplifier suffisamment, que p et q sont premiers entre eux, en particulier un seul d'entre eux est pair.
En élevant au carré, on obtient 2 = p2/q2, soit p2 = 2q2, en particulier p2 est pair. Le carré d'un nombre impair est impair, p est donc forcément pair, c'est-à-dire qu'il existe un entier k tel que p = 2k. En reportant dans l'égalité précédente et en simplifiant par 2, on obtient q2 = 2p2.
Toujours car le carré d'un nombre impair est impair, q est pair. Mais ceci contredit l'hypothèse de départ, qui est qu'au moins l'un des deux nombres p et q est impair.
Euclide n'exprimait pas les choses de cette façon (il ne parle pas du nombre √2 par exemple), mais sa démonstration arithmétique repose sur le même principe.Développement décimal illimité non périodique
Si les fractions permettent effectivement d'exprimer toute longueur avec la précision souhaitée, il faut néanmoins comprendre que les opérations et particulièrement la division deviennent complexes si le système de numération n'est pas adapté. Le problème est décrit par l'article fraction égyptienne qui propose quelques exemples concrets.
Il faut attendre le Ve siècle pour voir l'école indienne découvrir le concept du zéro et développer un système de numération décimal et positionnel.
Un deuxième problème apparaît alors. Toutes les fractions possèdent un développement décimal dans la mesure où ce développement est infini et périodique, c'est-à-dire que la suite des décimales ne s'arrête pas mais boucle sur un nombre fini de valeurs. La question se pose alors de savoir quel sens donner à un objet caractérisé par une suite de décimales non périodique. Par exemple, le nombre à développement décimal infini qui s'exprime comme
- 0,1010010001... où le nombre de 0 entre les chiffres 1 croît indéfiniment, correspond-il à une longueur ?
Suites et séries
Dans la deuxième moitié du XVIIe siècle, on assiste à un extraordinaire épanouissement des mathématiques dans le domaine du calcul des séries et des suites.
Nicolaus Mercator, les Bernoulli, James Gregory, Godfried Leibniz, et d'autres travaillent sur des séries qui semblent converger mais dont la limite n'est pas rationnelle. C'est le cas par exemple :
- de la série de Mercator :
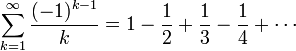
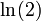
- de la série de Gregory :
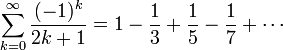
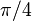
Pire, Liouville en 1844, prouve l'existence de nombres transcendants c'est-à-dire non racine d'un polynôme à coefficients entiers. Il ne suffit donc pas de compléter les rationnels en y ajoutant les nombres algébriques pour obtenir l'ensemble de tous les nombres.
- des séries du type
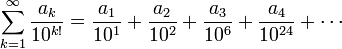
Le calcul infinitésimal
Durant la deuxième partie du XVIIe siècle, Isaac Newton et Gottfried Wilhelm Leibniz inventent une toute nouvelle branche des mathématiques. On l'appelle maintenant l'analyse, à l'époque elle était connue sous le nom de calcul infinitésimal. Cette branche acquiert presque immédiatement une renommée immense car elle est la base d'une toute nouvelle théorie physique universelle : la théorie de la gravité newtonienne. Une des raisons de cette renommée est la résolution d'une vieille question, à savoir si la Terre tourne autour du Soleil ou l'inverse.
Or le calcul infinitésimal ne peut se démontrer rigoureusement dans l'ensemble des nombres rationnels. Si les calculs sont justes, ils sont exprimés dans un langage d'une grande complexité et les preuves procèdent plus de l'intuition géométrique que d'une explicitation rigoureuse au sens de notre époque.
L'impossibilité de la construction de l'analyse dans l'ensemble des fractions réside dans le fait que cette branche des mathématiques se fonde sur l'analyse des infiniment petits. Or, on peut comparer les nombres rationnels à une infinité de petits grains de sable (de taille infiniment petite) sur la droite réelle laissant infiniment plus de trous que de matière. L'analyse ne peut se contenter d'un tel support. Elle demande pour support un espace complet. Le mot est ici utilisé dans un double sens, le sens intuitif qui signifie que les petits trous en nombre infini doivent être bouchés et le sens que les mathématiciens donnent aujourd'hui plus abstrait mais rigoureusement formalisé.
Cette notion est tellement importante qu'elle deviendra à l'aube du XXe siècle une large branche des mathématiques appelée topologie.
L'analyse suppose qu'une fonction réelle de la variable réelle est essentiellement connue par son comportement infinitésimal. Par exemple, si l'accélération d'une planète est connue à chaque instant et que sa position et sa vitesse initiales sont connues, alors il est possible d'en déduire la trajectoire exacte. Une chaîne de théorèmes, celle du théorème des accroissements finis qui se prouve par le théorème de Rolle qui se prouve par le théorème des bornes devient fausse sur les fractions rationnelles. Si on représente ce théorème en termes imagés, on peut décrire ces théorèmes de la manière suivante : pour le théorème des accroissements finis, si une voiture parcourt 120 km en 2 heures alors cette voiture se déplace au moins une fois à 60 km/h; pour le théorème de Rolle (respectivement le théorème des bornes), si une voiture part et arrive du même endroit sans jamais changer de route alors elle a fait au moins une fois demi-tour (respectivement il existe un moment où la voiture est le plus loin de son point de départ).
Ce sont ces théorèmes qui intuitivement sont si évidents, que l'on se demande même comment il est possible de les démontrer. Newton a poussé tellement loin les conséquences de ces évidences, que seules quelques rares personnes pouvaient à son époque véritablement comprendre son ouvrage majeur Philosophiae Naturalis Principia Mathematica. Les preuves se fondaient toujours in fine sur une intuition.
Explicitons alors pourquoi la démonstration du théorème des bornes impose une compréhension profonde de la nature topologique des nombres réels. Pour cela considérons la fonction f sur les rationnels de l'intervalle
![\left[1,3 \right]](https://static.techno-science.net/illustration/Definitions/autres/2/28432b66d7b98a7c8a5b47cda15f001c_ea75aec13af962d26da9dd0647d5366f.png)





La droite réelle
Si l'existence des nombres négatifs apparaît très tôt dans l'histoire (mathématiques indiennes), il faut attendre 1770 pour qu'ils obtiennent grâce à Euler un vrai statut de nombre et perdent leur caractère d'artifice de calcul. Mais il faut attendre encore un siècle pour voir l'ensemble des réels associé à l'ensemble des points d'une droite orientée, appelée droite réelle.
On considère une droite D contenant un point O que l'on appellera, par convention, origine. Soit un point I distinct de O appartenant à D que l'on identifie au nombre 1. Par convention, on dira que la distance de O à I est égale à 1 et que l'orientation de la droite est celle de O vers I. À tout point M de la droite, on associe la distance entre O et M. Si M et I sont du même côté par rapport à O alors la distance est comptée positivement, sinon elle est négative.
Cette relation que la formalisation actuelle appelle bijection permet d'identifier un nombre réel à un point d'une droite.

Après 2200 ans : la solution
Le développement de l'analyse au cours des XVIIIe et XIXe siècles a conduit les mathématiciens français et allemands à s'interroger sur la nature des nombres réels. Ces interrogations les ont conduit à dégager des propriétés fondamentales (complétude, suites adjacentes, etc) sur lesquelles pouvaient se fonder les constructions possibles de R, qui ont été formalisées autour de 1870 par Cantor, Méray et Dedekind.
La construction
Dans son cours d'Analyse à l'École Polytechnique, Augustin Cauchy propose la première définition rigoureuse d'une limite. Une séquence de nombres réels indexée par les entiers naturels (appelé suite) converge vers une limite (nécessairement unique) x lorsque la distance |x-xn| devient aussi petite que souhaitée pour n suffisamment grand. Il énonce un critère qui porte aujourd'hui son nom, le critère de Cauchy : il faut et il suffit que les distances |xn-xm| soient aussi petites que souhaitées pour n et m suffisamment grands. Par l'énoncé de ce critère, Cauchy affirme la complétude du corps des nombres réels, propriété sur laquelle peut être fondée sa définition. Cette approche est formalisée par Méray en 1869 puis par Cantor en 1883 ou en 1872. Cette idée, particulièrement adaptée à l'analyse, trouve des prolongements dans les méthodes de complétion.
Une seconde construction est publiée par Richard Dedekind en 1872. Elle découle de l'étude de la relation d'ordre sur les fractions. Une coupure de Dedekind est un ensemble A de rationnels, tel que tout rationnel de A est inférieur à tout rationnel du complémentaire de A. Un réel est alors représenté par une coupure de Dedekind. Par exemple, la racine carrée de 2 est représenté par l'ensemble des rationnels négatifs et des rationnels positifs de carrés inférieurs à 2. Il existe des variantes de la définition de coupure selon les auteurs.
Une troisième construction s'appuie sur la méthode des segments emboîtés. Un emboîtement est une suite décroissante d'intervalles fermés de nombres rationnels dont la longueur tend vers 0. Un nombre réel est alors défini comme une classe d'emboîtements modulo une relation d'équivalence. Selon Mainzer, « la vérification des propriétés de corps ordonnée est relativement pénible », ce qui explique pourquoi cette approche apparaît moins avantageuse que les deux précédentes. Il existe aussi une autre méthode à partir des développements décimaux, cependant l'addition puis la multiplication ne sont pas des opérations simples à définir.
En 1899, David Hilbert donne la première définition axiomatique du corps des nombre réels. Les méthodes précédentes construisent toutes le « même » ensemble, celui des nombres réels.
La solution est plus riche que prévue
Le XIXe siècle montre que cette nouvelle structure, l'ensemble des nombres réels, ses opérations et sa relation d'ordre, non seulement remplit ses promesses mais va au-delà.
- Non seulement le paradoxe de la
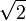
![x \mapsto \sqrt[n]{x}](https://static.techno-science.net/illustration/Definitions/autres/8/8b58c368f9187e90b33e6ebbe66047dc_4d6c7e89200bb7285fc54cf3beefbdf7.png)
- Les développements décimaux infinis ont maintenant un sens. De plus, il devient possible de mieux comprendre les nombres réels et de les classifier. Ainsi, en dehors des fractions rationnelles on découvre le corps des nombres algébriques, c'est-à-dire des nombres qui sont racines d'un polynôme à coefficients entiers. Une nouvelle famille de nombres est exhibée : les transcendants qui ne sont racines d'aucune équation polynomiale à coefficients entiers. Les propriétés de ces nombres permettent la démonstration de vieilles conjectures comme la quadrature du cercle.
- Enfin, le Théorème de Rolle est généralisé et permet la démonstration d'un résultat essentiel pour l'analyse. Le comportement infinitésimal d'une fonction, par exemple le fait que la dérivée soit toujours positive, permet de déduire un comportement global. Cela signifie par exemple, que si un solide se déplace sur une droite avec une vitesse instantanée toujours positive, alors le solide a avancé, c'est-à-dire qu'il s'est déplacé positivement (vers « l'avant ») par rapport à l'origine. Cette question qui avait arrêté les Grecs, incapables de résoudre les paradoxes de Zénon, est définitivement comprise. Ce résultat, que l'intuition déclare évident, a demandé des siècles d'efforts.
- Dans le développement du calcul infinitésimal, la manipulation des infiniment petits peut alors être abordée différemment. L'ensemble des nombres réels ne pourra satisfaire tous les mathématiciens. Dans les années 1960, Abraham Robinson met en place la notion de nombre hyperréel et permet le développement de l'analyse non standard. Cette nouvelle théorie permet d'exprimer et de démontrer plus simplement certains résultats fondamentaux comme le Théorème de Bolzano-Weierstrass.