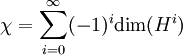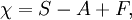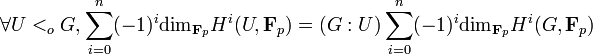Caractéristique d'Euler - Définition

La caractéristique d'Euler — ou d'Euler-Poincaré — est un invariant numérique, un nombre qui décrit un aspect d'une forme de l'espace topologique ou de la structure. Elle est communément notée par .

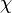
La caractéristique d'Euler fut définie à l'origine pour les polyèdres et fut utilisée pour démontrer divers théorèmes les concernant, incluant la classification des solides de Platon. Leonhard Euler, par qui le concept eut son nom, fut responsable pour beaucoup dans ce travail de pionnier. En mathématiques plus modernes la caractéristique d'Euler apparait dans l'homologie et les méthodes cohomologiques. Elle est donnée en général par la somme alternée des dimensions des groupes de cohomologie considérés :

Polyèdres

La caractéristique d'Euler a été définie de manière classique pour les polyèdres, selon la formule

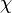
où S, A et F sont respectivement le nombres de sommets (coins), d'arêtes et de faces dans un polyèdre donné. Pour un polyèdre quelconque homéomorphe à une sphère, la caractéristique d'Euler s'avère être

.

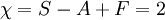
Ce résultat est connu sous le nom formule d'Euler.

Exemples de polyèdres convexes

La surface d'un polyèdre convexe est homéomorphe à une sphère et par conséquent possède une caractéristique d'Euler égale à 2, par la formule d'Euler. Ce fait peut être utilisé pour montrer qu'il existe seulement cinq solides de Platon (polyèdre régulier) :

Nom	Image	S (sommets)	A (arêtes)	F (faces)	Caractéristique d'Euler : S - A + F
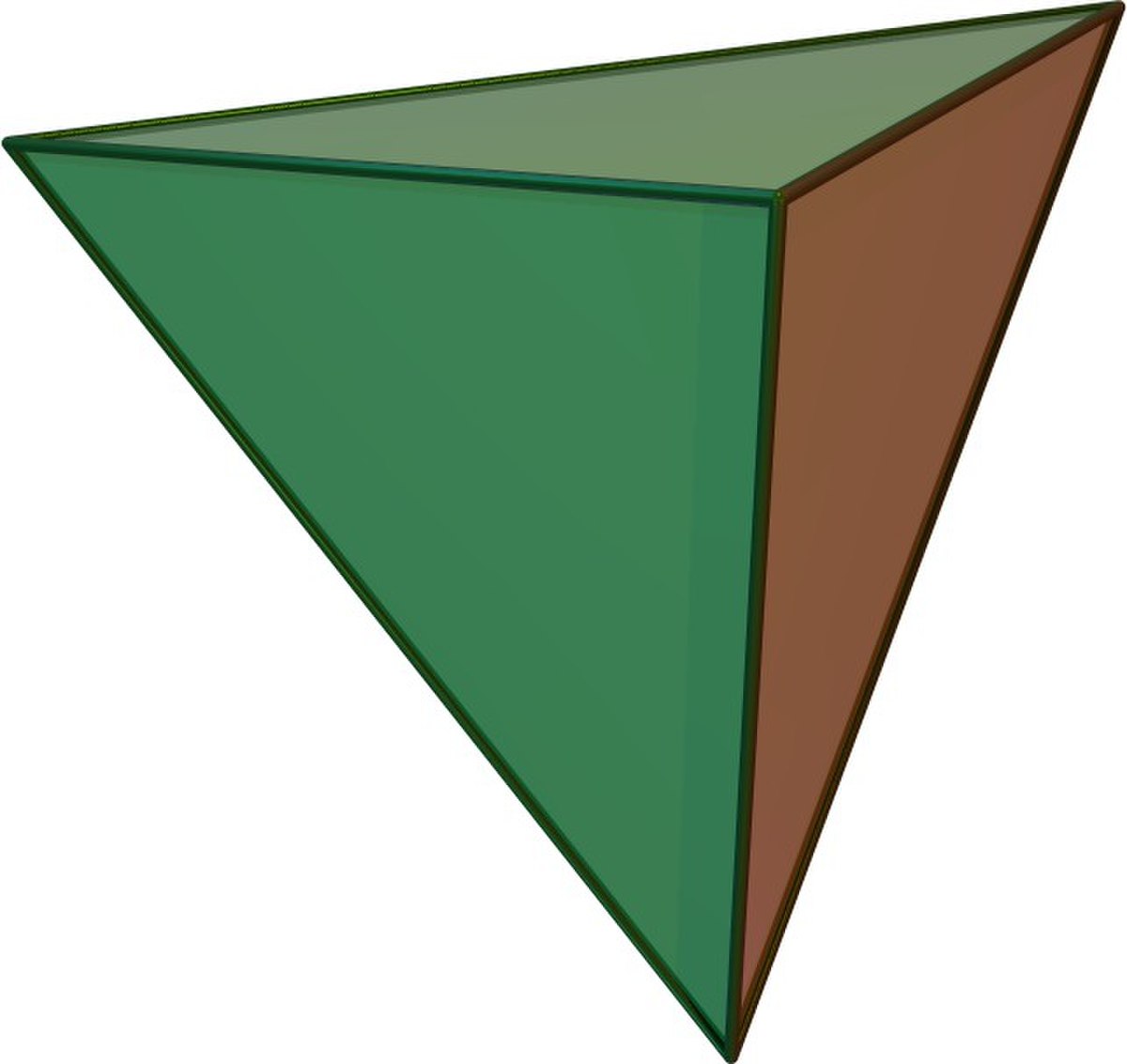
Tétraèdre		4	6	4	2
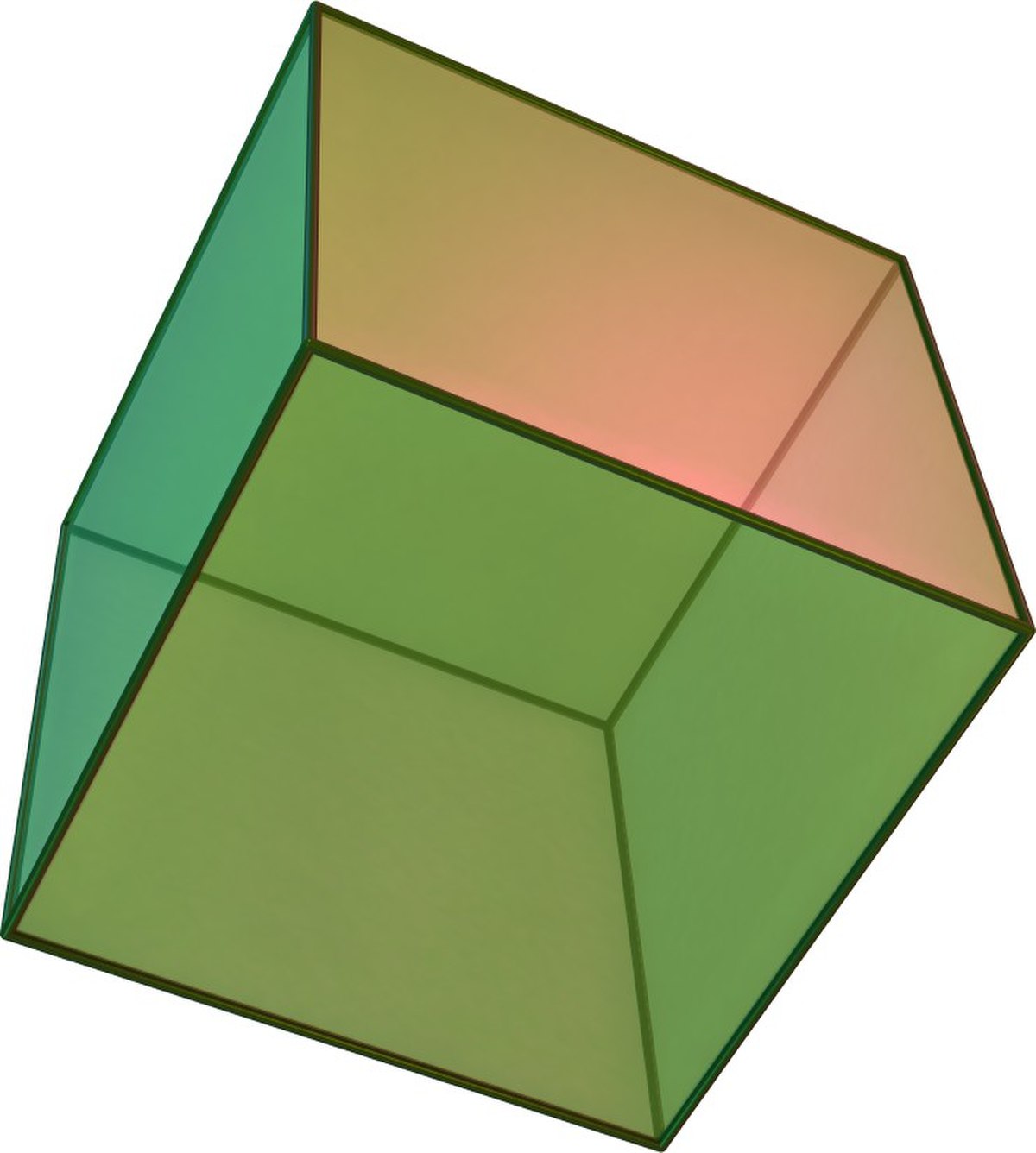
Hexaèdre ou cube		8	12	6	2
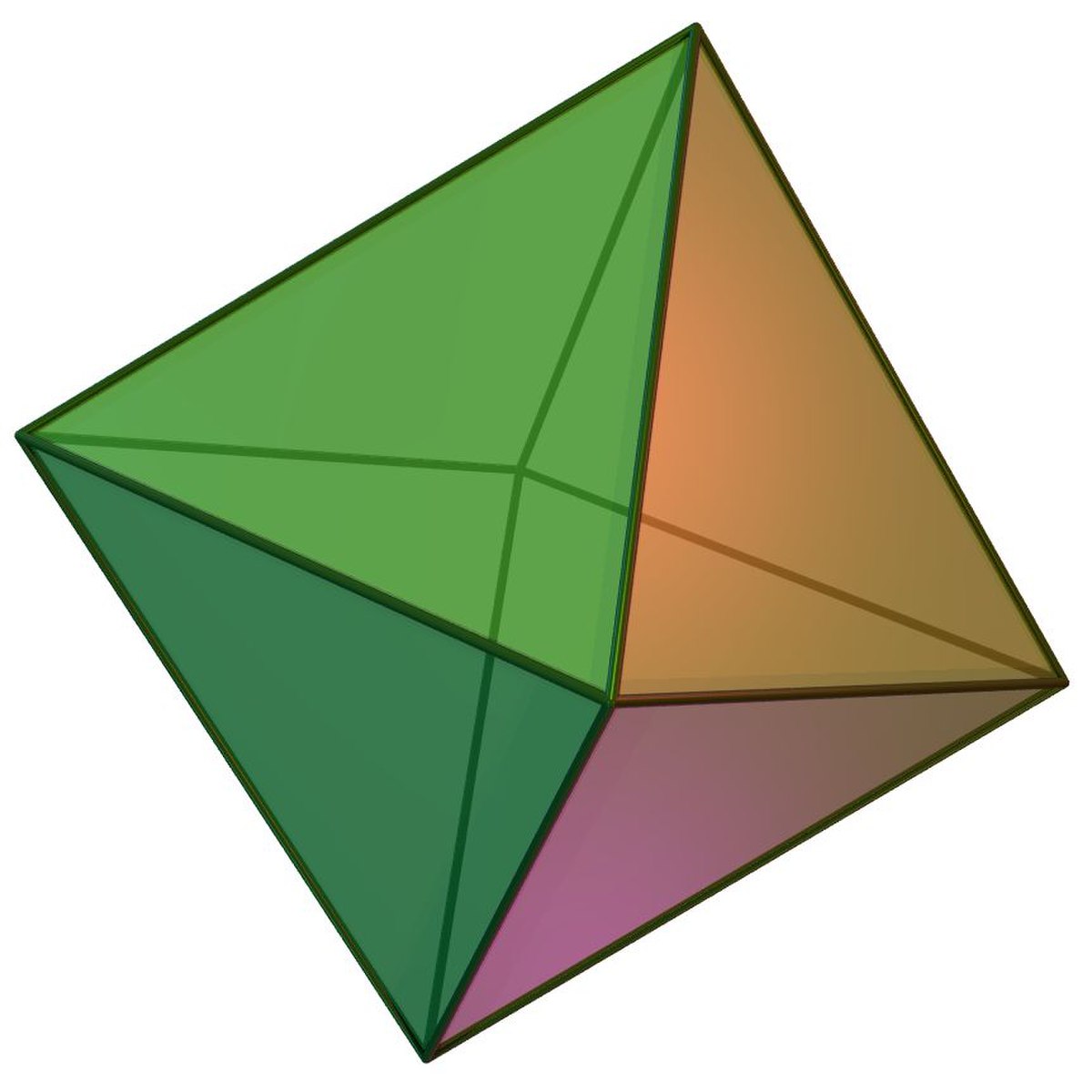
Octaèdre		6	12	8	2
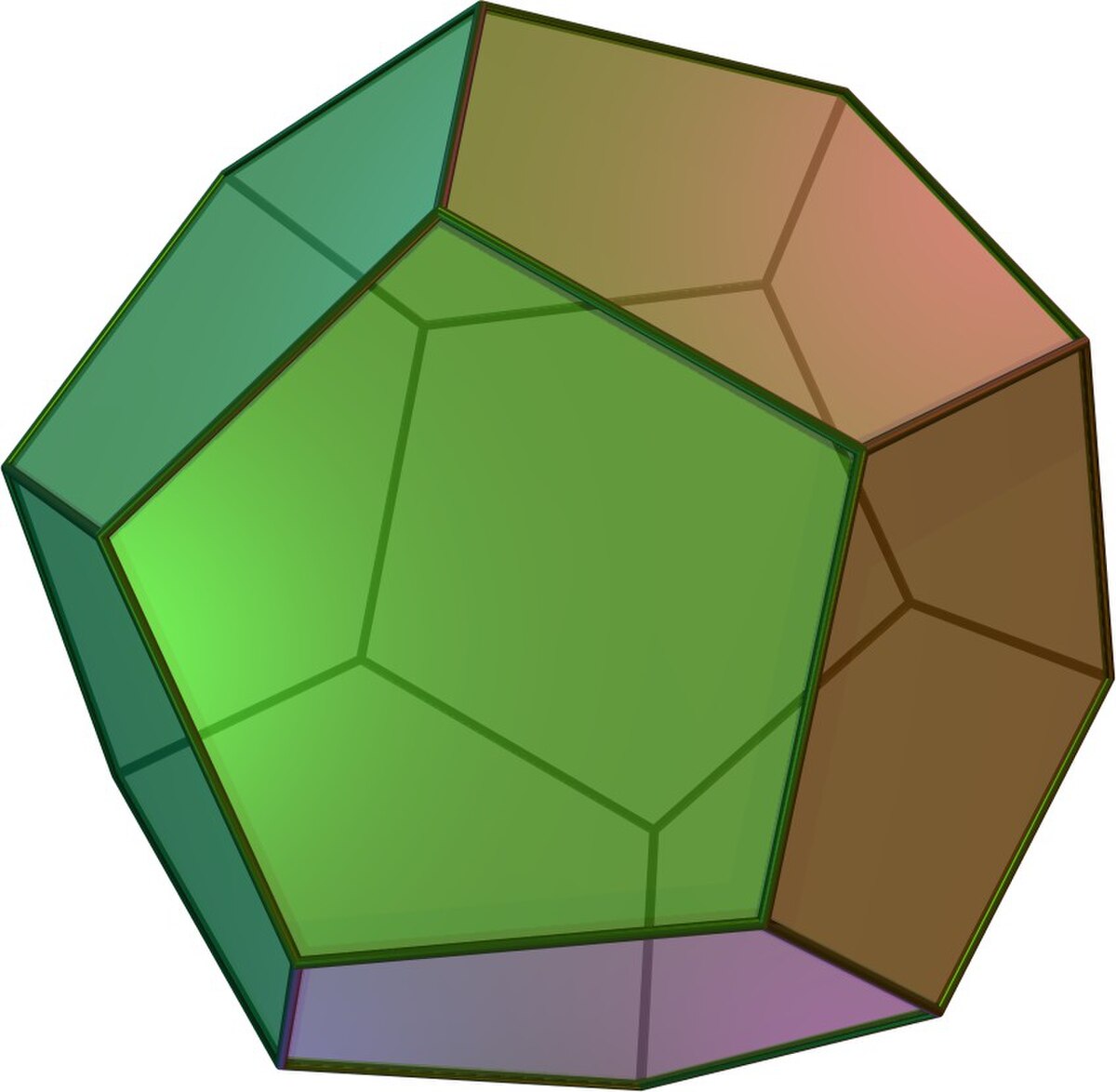
Dodécaèdre		20	30	12	2
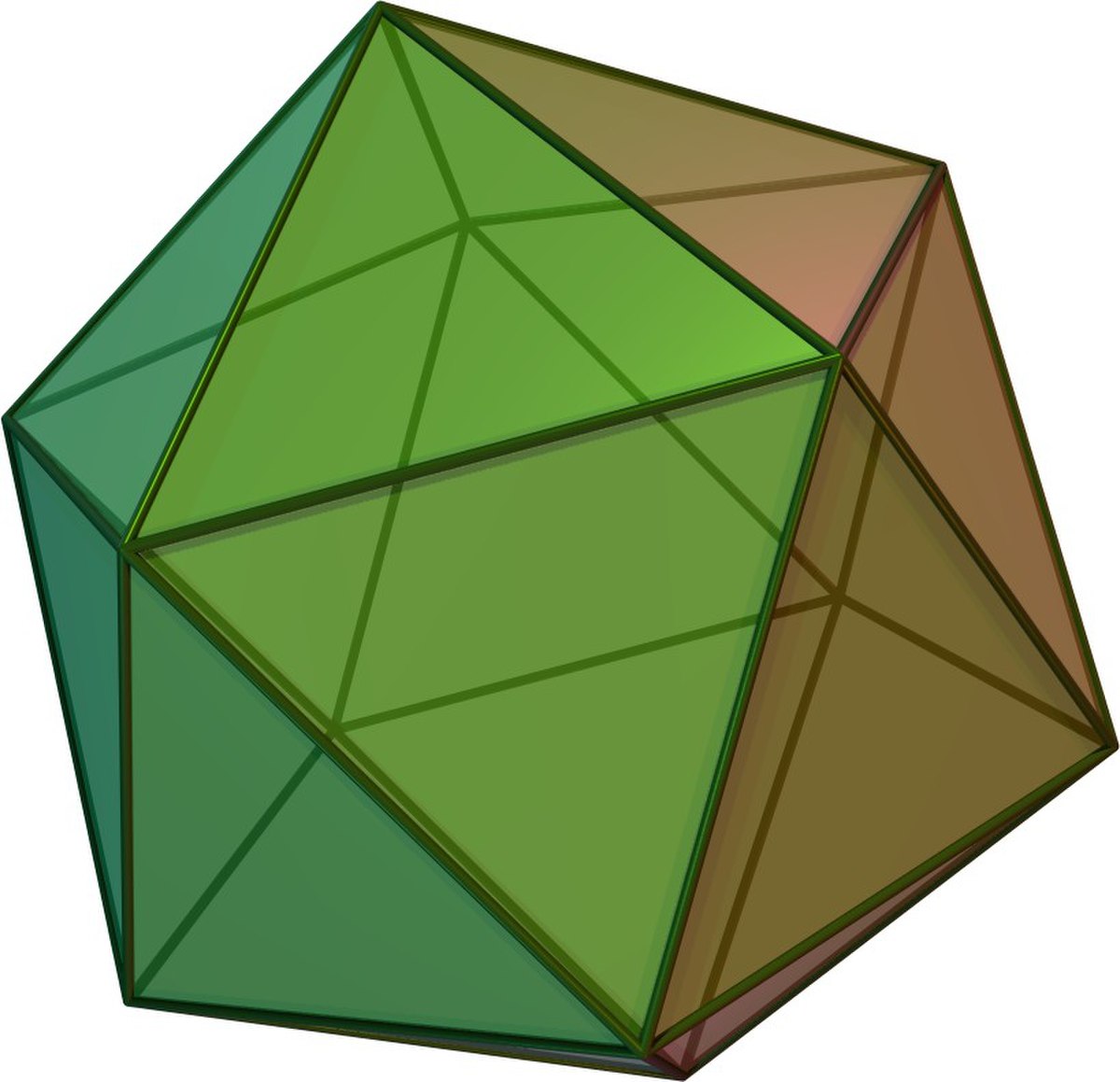
Icosaèdre		12	30	20	2

Exemples de polyèdres non-convexes

Les polyèdres non-convexes peuvent avoir diverses caractéristiques d'Euler :

Nom	Image	S (sommets)	A (arêtes)	F (faces)	Caractéristique d'Euler : S - A + F
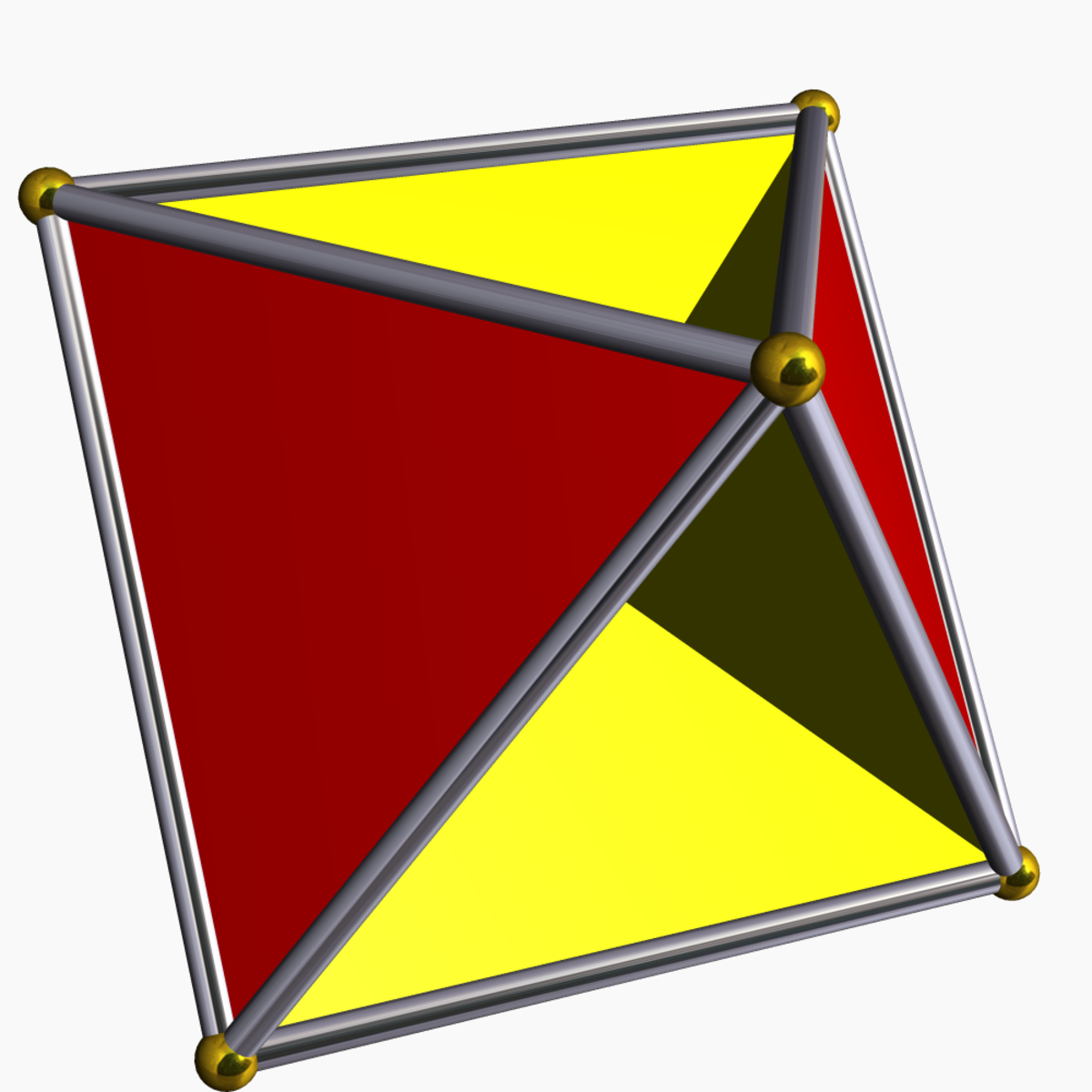
Tétrahémihexaèdre		6	12	7	1
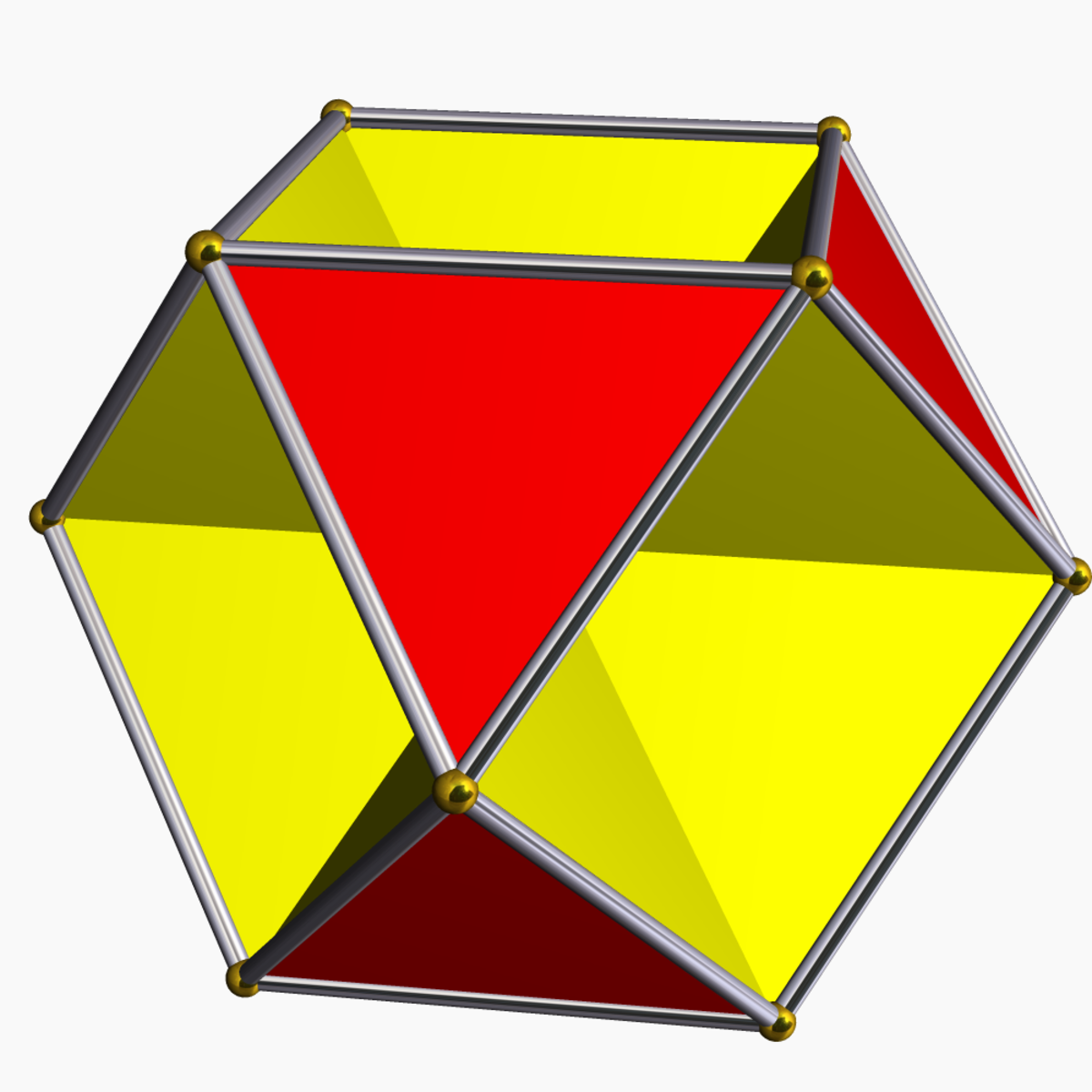
Octahémioctaèdre		12	24	12	0
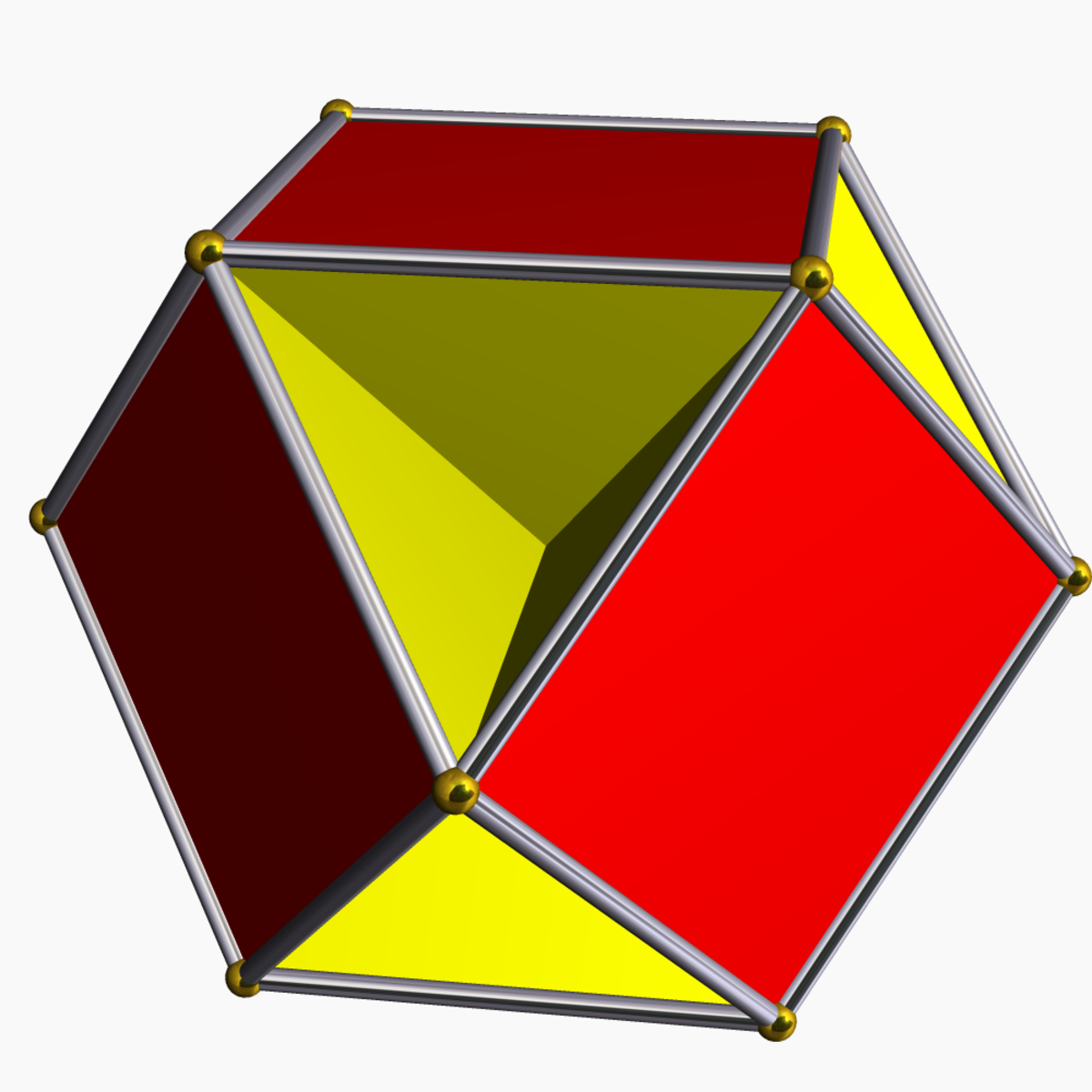
Cubohémioctaèdre		12	24	10	-2

Définition formelle

Les polyèdres discutés ci-dessus sont, en langage moderne, des complexes CW finis à deux dimensions. (lorsque seules les faces triangulaires sont utilisées, ils sont appelés complexes simpliciaux finis à deux dimensions). En général, pour un complexe-CW fini quelconque, la caractéristique d'Euler peut être définie comme la somme alternée :

,

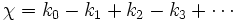
où k_n désigne le nombre de cellules de dimensions n dans le complexe.

Plus généralement encore, pour un espace topologique quelconque, nous pouvons définir le n^e nombre de Betti b_n comme le rang du n^e groupe homologique. La caractéristique d'Euler peut être définie comme la somme alternée

.

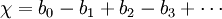
Cette quantité est bien définie si les nombres de Betti sont tous finis et s'ils sont égaux à zéro au-delà d'un certain indice n₀. Cette définition englobe les précédentes.

Théorie des groupes

Dans le cas de la cohomologie des pro-p-groupes, la caractéristique d'Euler permet par exemple de caractériser la dimension cohomologique : soit G un pro-p- groupe, alors, G est de dimension cohomologique inférieure à n si et seulement si la caractéristique d'Euler tronquée à l'ordre n est multiplicative à travers les sous-groupes ouverts de G, c'est-à-dire si et seulement si :

Topologie algébrique

Définition

En topologie algébrique, la caractéristique d'Euler d'une variété, notée c ou encore χ (Chi), est la somme alternée des nombres de Betti, comme indiqué ci-dessus. En particulier, c = 2 pour le plan projectif et la sphère, c = 1 pour le disque du plan et c = 0 pour le tore et la bouteille de Klein.

Propriétés

Un espace contractible quelconque, (c’est-à-dire, un équivalent homotopique à un point) possède une homologie triviale, ce qui signifie que le 0^e nombre de Betti est 1 et les autres 0. Par conséquent, sa caractéristique d'Euler est 1. Ce case inclut l'espace euclidien de dimension quelconque, autant que la boule solide unitaire dans un espace euclidien quelconque — l'intervalle à une dimension, le disque à deux dimensions, la boule à trois dimensions, etc.

La caractéristique d'Euler peut être calculée facilement pour des surfaces générales par un maillage sur la surface (c’est-à-dire, une description sous la forme d'un complexe CW). Pour un objet, elle représente le nombre de singularités nécessaires pour mailler cet objet avec ses géodésiques.

Exemples

• La sphère a pour caractéristique 2 : elle possède deux pôles.
• Le tore a une caractéristique nulle : il est possible de le mailler sans introduire de singularité.

Nom	Image	caractéristique d'Euler
Sphère		2
Tore		0
ruban de Möbius		0
bouteille de Klein		0
Deux sphères (non connexe)		2 + 2 = 4