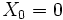Générateur de nombres pseudo-aléatoires - Définition

Un générateur de nombres pseudo-aléatoires est un algorithme qui génère une séquence de nombres présentant certaines propriétés du hasard. Par exemple, les nombres sont supposés être approximativement indépendants les uns des autres, et il est potentiellement difficile de repérer des groupes de nombres qui suivent une certaine règle (comportements de groupe).

Cependant, les sorties d'un tel générateur ne sont pas entièrement aléatoires ; elles s'approchent seulement des propriétés idéales des sources complètement (Le complètement ou complètement automatique, ou encore par anglicisme complétion ou...) aléatoires. John von Neumann (John von Neumann (né Neumann János, 1903-1957), mathématicien et physicien...) insista sur ce fait avec la remarque suivante : " Quiconque considère des méthodes arithmétiques pour produire des nombres aléatoires est, bien sûr, en train (Un train est un véhicule guidé circulant sur des rails. Un train est composé de...) de commettre un péché ". De vrais nombres aléatoires peuvent être produits avec du matériel qui tire parti de certaines propriétés physiques stochastiques (bruit d'une résistance par exemple).

La raison pour laquelle on se contente d’un rendu (Le rendu est un processus informatique calculant l'image 2D (équivalent d'une photographie)...) pseudo-aléatoire est : d’une part qu’il est difficile d’obtenir de " vrais " nombres aléatoires et que, dans certaines situations, il est possible d’utiliser des nombres pseudo-aléatoires, en lieu et place de vrais nombres aléatoires ; d’autre part, que ce sont des générateurs particulièrement adaptés à une implémentation (Le mot implantation peut avoir plusieurs significations :) informatique (L´informatique - contraction d´information et automatique - est le domaine...), donc plus facilement et plus efficacement utilisables.

Les méthodes pseudo-aléatoires sont souvent employées sur des ordinateurs, dans diverses tâches comme la méthode de Monte-Carlo (Le terme méthode de Monte-Carlo désigne toute méthode visant à calculer une...), la simulation ou les applications cryptographiques. Une analyse mathématique (Les mathématiques constituent un domaine de connaissances abstraites construites à l'aide...) rigoureuse est nécessaire pour déterminer le degré (Le mot degré a plusieurs significations, il est notamment employé dans les domaines...) d'aléa d'un générateur pseudo-aléatoire. Robert R. Coveyou du Oak Ridge National Laboratory écrivit dans un article que " la génération de nombres aléatoires est trop importante pour être confiée au hasard ".

La plupart des algorithmes pseudo-aléatoires essaient de produire des sorties qui sont uniformément distribuées. Une classe très répandue de générateurs utilise une congruence linéaire. D'autres s'inspirent de la suite de Fibonacci (Leonardo Fibonacci (Pise, v. 1170 - v. 1250) est un mathématicien italien. Fibonacci (de son nom...) en additionnant deux valeurs précédentes ou font appel à des registres à décalage dans lesquels le résultat précédent est injecté après une transformation intermédiaire. Certains générateurs pseudo-aléatoires sont dits cryptographiques quand certaines contraintes sont satisfaites. Citons entre autres Fortuna, Yarrow (Yarrow est un générateur cryptographique de nombres pseudo-aléatoires inventé par Bruce...) ou Blum Blum Shub (Blum Blum Shub (BBS) est un algorithme capable de générer des nombres pseudo-aléatoires. Il fut...).

Problèmes expliquant le terme " pseudo-aléatoire "

Utiliser des algorithmes pour créer des nombres aléatoires, sachant ce qu’est un algorithme, peut paraître assez douteux. De plus, étant donné qu’on ne sait pas bien définir le caractère aléatoire, on se demande comment on peut ne serait-ce que vouloir produire une séquence aléatoire à l’aide d’algorithmes.

Ces reproches sont tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou...) à fait fondés et on ne peut les nier. Ce sont les raisons pour lesquelles on parle de générateurs de nombres pseudo-aléatoires. En pratique, il est possible de limiter les conséquences négatives de l’utilisation d’une méthode algorithmique (L'algorithmique est l’ensemble des règles et des techniques qui sont impliquées...) pour générer des nombres aléatoires.

Biais inhérent aux méthodes employées

Comme un générateur de nombres aléatoires (Un générateur de nombres aléatoires, random number generator (RNG) en anglais, est...) est exécuté sur un ordinateur (Un ordinateur est une machine dotée d'une unité de traitement lui permettant...) déterministe, il devient de facto un algorithme déterministe. Ses sorties sont inévitablement entachées d'une caractéristique absente d'une vraie suite aléatoire : la périodicité. Avec des ressources limitées (mémoire, nombre (La notion de nombre en linguistique est traitée à l’article « Nombre...) de registres, etc.), le générateur retrouvera le même état interne (En France, ce nom désigne un médecin, un pharmacien ou un chirurgien-dentiste, à la...) au moins deux fois. Après coup, il entrera obligatoirement dans un cycle. Un générateur non périodique n'est pas impossible, mais nécessite une mémoire (D'une manière générale, la mémoire est le stockage de l'information. C'est aussi le souvenir...) croissante pour ne pas se retrouver dans le même état. Pour contourner cet obstacle théorique, le générateur peut commencer dans un état quelconque (la " graine "). Il produira toutefois la même suite si la graine (Dans le cycle de vie des « plantes à graines », la graine est la structure qui...) reste identique. De plus, le nombre de graines possibles n'est pas infini (Le mot « infini » (-e, -s ; du latin finitus,...) et le générateur ne peut produire qu'un nombre limité de séquences différentes.

Pour améliorer la qualité des sorties, on peut introduire des composantes " aléatoires " provenant des imperfections du système, comme par exemple le temps (Le temps est un concept développé par l'être humain pour appréhender le...) entre deux accès au disque dur (Un disque dur est une mémoire de masse magnétique utilisée principalement dans les...) ou le nombre de millisecondes depuis le lancement de l'ordinateur. Ces valeurs sont toutefois comprises entre certains intervalles et/ou sont en partie prévisibles. Le système reste pseudo-aléatoire.

Déviation par rapport au hasard (Dans le langage ordinaire, le mot hasard est utilisé pour exprimer un manque efficient, sinon...) parfait

La longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus...) de la période maximale double à chaque fois qu'un bit (Le bit est un chiffre binaire, c'est-à-dire 0 ou 1. Il est donc aussi une unité de mesure...) est ajouté à l'état interne. Il est facile de construire des générateurs pseudo-aléatoires avec une période plus longue que ce que n'importe quel ordinateur pourrait calculer. Mersenne Twister (Développé par Makoto Matsumoto et Takuji Nishimura en 1997, le Mersenne Twister est un...), un excellent générateur de nombres aléatoires pour les applications non cryptographiques, a une période prouvée mathématiquement de 2¹⁹⁹³⁷ - 1, un nombre astronomique.

La question est ouverte quant à savoir s'il est possible de distinguer une suite pseudo-aléatoire générée algorithmiquement d'une source parfaite d'aléa, et ceci sans connaître la graine du générateur. En cryptographie (La cryptographie est une des disciplines de la cryptologie s'attachant à protéger des messages...), la plupart des spécialistes partent du principe que c'est une chose impossible avec la puissance (Le mot puissance est employé dans plusieurs domaines avec une signification particulière :) de calcul actuelle. Ce principe est utilisé pour les chiffrements par flot comme RC4 qui procède à un XOR entre une suite pseudo-aléatoire et les données (Dans les technologies de l'information (TI), une donnée est une description élémentaire, souvent...).

En principe, la plupart des générateurs ont des problèmes mathématiques qui peuvent être décelés avec une analyse statistique (La statistique est à la fois une science formelle, une méthode et une technique. Elle...). La qualité des sorties augmente souvent au détriment de la vitesse (On distingue :) de génération et ces paramètres doivent être considérés lors de l'utilisation d'un générateur. Les failles peuvent être les suivantes :

• période plus courte avec certaines graines
• qualité du générateur qui varie fortement selon la graine
• distribution imparfaite, manque d'uniformité
• mauvaise distribution dans un espace de dimension (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce...) supérieure à 1
• ou au contraire : distribution trop idéale, uniformité trop parfaite
• valeurs successives qui ne sont pas indépendantes (ce qui est toujours le cas, sauf si on injecte des données, issues de sources aléatoires, dans une étape de la génération)
• certains bits dans les sorties sont moins aléatoires (par exemple, le bit n°8 reste souvent à 1)

Les défauts peuvent être importants ou quasiment invisibles. L'algorithme RANDU (RANDU est le nom d'un générateur congruentiel linéaire utilisé dans les années 60, sur des...) utilisé pendant plusieurs décennies était biaisé et certains résultats obtenus à l'époque ne peuvent être complètement validés. Il arrive parfois qu'une application pratique permette de déceler le problème (par exemple une simulation physique (La physique (du grec φυσις, la nature) est étymologiquement la...) avec des résultats complètement inattendus), mais il est préférable de faire des tests avant utilisation pour les déceler.

Historique du développement des générateurs pseudo-aléatoires

Le développement des algorithmes générant des nombres pseudo-aléatoires est très lié à celui de la cryptographie, l’importance militaire et économique de cette science (La science (latin scientia, « connaissance ») est, d'après le dictionnaire...) ayant motivé de nombreuses recherches au cours de l’histoire.

Les cryptages utilisés traditionnellement jusqu’au XIXème siècle (Un siècle est maintenant une période de cent années. Le mot vient du latin saeculum, i, qui...) reposaient essentiellement sur le secret autour (Autour est le nom que la nomenclature aviaire en langue française (mise à jour) donne...) de la méthode utilisée, et sur l’absence de traitement de masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un...). De nos jours, de telles méthodes sont impraticables car il existe de nombreuses théories statistiques qui permettent de retrouver l’algorithme de génération à partir de ses résultats. En outre, les techniques de cryptage (En cryptographie, le chiffrement (parfois appelé à tort cryptage) est le procédé grâce auquel...) ne peuvent plus être gardées secrètes, et en 1883, Auguste Kerckhoffs exposera une règle fondamentale (En musique, le mot fondamentale peut renvoyer à plusieurs sens.) de la cryptographie moderne : la sécurité d’un système ne doit pas reposer sur la méconnaissance de la méthode de cryptage. Cette règle, accompagnée par le développement des algorithmes de chiffrement (En cryptographie, le chiffrement (parfois appelé à tort cryptage) est le procédé grâce auquel...) par clé, marquera le début de l’essor des générateurs pseudo-aléatoires.

Leur importance est toutefois restée limitée tant que les moyens physiques de calcul n’ont pu supporter les longs et répétitifs calculs qu’ils nécessitent. C’est pourquoi leur émergence n’a vraiment commencé qu’en 1946, quand John Neumann publie son générateur middle-square. C'est durant les années qui suivirent que la plupart des algorithmes rapides et populaires virent le jour : en 1948 D. H. Lehmer introduit les générateurs congruentiels linéaires qui seront améliorés en 1958 par G.J. Mitchell et D.P. Moore ; et deviendront par la suite extrêmement répandus, la plupart des fonctions de cryptage basique y ayant recours.

Ces premiers générateurs pseudo-aléatoires possèdent malgré leur large popularité des propriétés statistiques assez mauvaises, et ne répondaient pas aux besoins des cryptographes. Plus récemment, des algorithmes robustes vis-à-vis des analyses statistiques ont été élaborés, comme l’algorithme Mersenne Twister (1997) ou encore la Méthode de Fibonacci lacunaire.

Mais aucun algorithme pseudo-aléatoire ne peut vraiment générer de suite à l’abri de toute analyse statistique (Une statistique est, au premier abord, un nombre calculé à propos d'un échantillon....), en particulier car la " graine " doit en théorie (Le mot théorie vient du mot grec theorein, qui signifie « contempler, observer,...) être elle-même aléatoire, et l’algorithme utilisé ne peut s’initialiser lui-même. Les générateurs cryptographiques actuels sont donc obligés de faire intervenir une part de hasard qui n’est pas générée par un moyen déterministe : on s’oriente vers des générateurs hybrides, possédant un algorithme de génération de nombres pseudo-aléatoires robuste, et s’initialisant sur un moyen physique de production de hasard.

Exemples d'algorithmes connus

La méthode de Von Neumann

En 1946, John von Neumann propose un générateur pseudo-aléatoire connu sous le nom de la méthode middle-square (carré médian). Très simple, elle consiste à prendre un nombre, à l'élever au carré (Un carré est un polygone régulier à quatre côtés. Cela signifie que ses...) et à prendre les chiffres au milieu comme sortie. Celle-ci est utilisée comme graine pour l'itération suivante.

Exemple

Soit le nombre " 1111 ".

1. 1111² = 1234321
2. on récupère les chiffres du milieu : 3432. C'est la sortie du générateur.
3. 3432² = 11778624
4. on récupère les chiffres du milieu : 7786.

et ainsi de suite.

Défauts

Von Neumann utilisa des nombres comportant 10 chiffres, le principe restant le même. Toutefois, la période du middle-square est faible. La qualité des sorties dépend de la graine, " 0000 " produit toujours la même séquence et constitue un " état absorbant " de l'algorithme. Von Neumann en était conscient, mais il craignait que des retouches a priori nécessaires n'apportent d'autres vices cachés. Sur l'ordinateur ENIAC qu'il utilisait avec sa méthode, il obtenait une génération 200 fois plus rapide que les résultats obtenus avec des cartes perforées. Selon Von Neumann, les générateurs basés sur du matériel ne pouvaient pas fonctionner correctement car il ne stockait pas les résultats (et on ne pouvait donc pas les vérifier). La méthode de Von Neumann montra vite ses limites lors d'applications utilisant des méthodes statistiques comme celle de Monte Carlo.

Méthode de Fibonacci

Cette méthode est basée sur la suite de Fibonacci modulo ( En arithmétique modulaire, on parle de nombres congrus modulo n Le terme modulo peut aussi...) la valeur maximale désirée :

avec x(0) et x(1) en entrée.

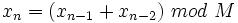
On peut employer une variante :

avec x(1)....x(k-1) en entrée.

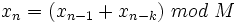
La qualité du générateur dépend de et des nombres utilisés pour initialiser la suite. Ce générateur est par contre très simple à implémenter et ne consomme que peu de ressources.

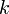
Générateurs congruentiels linéaires

Introduits en 1948 par D. H. Lehmer sous une forme réduite (incrément nul), ils vont être généralisés et seront largement utilisés ensuite. Ils reposent sur une simple formule de récurrence :

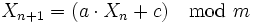
avec la graine (seed en anglais : un nombre employé pour produire une suite pseudo-aléatoire habituellement plus longue). En général, la graine est un nombre premier (Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et...), mais les contraintes exactes à son sujet dépendent de l'algorithme. Certaines graines peuvent conduire à des séquences dégénérées.

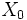
La période de ce générateur est au maximum de m, c’est-à-dire qu’elle est relativement courte puisque m est souvent choisi de manière à être de l’ordre de la longueur des mots sur l’ordinateur (par exemple : 2³² sur une machine 32 bits). Mais cette méthode présente un avantage : on connaît les critères sur les nombres a, c et m qui vont permettre d’obtenir une période maximale (égale à m).

Exemples d'algorithmes

Algorithme	a	c	m	Remarques
RANDU	65539	0	231	Biaisé et fortement déconseillé
générateur de Robert Sedgewick (Robert Sedgewick est un informaticien états-unien, surtout connu pour sa série de manuels...)	31415821	1	108	Intéressant mais déconseillé (essayer avec )
Standard minimal	16807	0	231-1

D’autres exemples utilisant les congruences

L'itération de Lehmer n'est pas la seule possible ; on peut notamment utiliser d'autres formes de congruence :

• avec
• (pour j, k fixés)

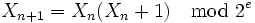
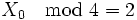
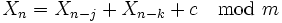
En particulier : proposée en 1958 par G.J. Mitchell et D.P. Moore a passé avec succès de nombreux tests statistiques ; on sait par ailleurs que cette suite possède une très longue période. Son plus gros défaut est l’absence de théorie la concernant. Ici encore, les valeurs initiales sont cruciales. Si les sont nuls pour tout n appartenant à l'ensemble (En théorie des ensembles, un ensemble désigne intuitivement une collection...) initial, alors la suite produira toujours un résultat nul.

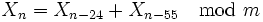
Mersenne Twister

Inventé par Makoto Matsumoto et Takuji Nishimura en 1997, Mersenne Twister est particulièrement réputé pour sa qualité. Avec sa période de 2¹⁹⁹³⁷-1 itérations, il distribue de manière uniforme sur 623 dimensions (pour des nombres de 32 bits) et s'avère être plus rapide que la plupart des méthodes statistiquement plus faibles. Il est toutefois possible d'analyser la sortie de Mersenne Twister et de se rendre compte qu'il n'est pas entièrement aléatoire. L'algorithme de Berlekam-Massey ou l'algorithme de Reed-Sloane permettent de répondre à cette question. À ce jour (Le jour ou la journée est l'intervalle qui sépare le lever du coucher du Soleil ; c'est la...), les seuls effets négatifs sont liés à la cryptographie, Mersenne Twister ne pouvant accéder au titre de générateur cryptographique.

Générateurs pseudo-aléatoires cryptographiques

Certains générateurs pseudo-aléatoires peuvent être qualifiés de cryptographiques quand ils font preuve de certaines propriétés nécessaires pour qu’ils puissent être utilisés en cryptologie. Ils doivent être capables de produire une sortie suffisamment peu discernable d’un aléa parfait et doivent résister à des attaques comme par exemple l'injection (Le mot injection peut avoir plusieurs significations :) de données forgées de manière à produire des imperfections dans l'algorithme, ou encore des analyses statistiques qui permettraient de prédire la suite.

Dans la catégorie des générateurs suffisamment sûrs, on trouve :

• Yarrow
• Fortuna
• Blum Blum Shub (sûr mais lent)
• ISAAC (ISAAC est un algorithme capable de générer des nombres pseudo-aléatoires, tombé dans le domaine...)

Une méthode courante pour générer de l'aléa en cryptographie consiste à " accumuler de l'entropie " (via diverses sources disponibles sur un ordinateur : temps entre deux accès au disque (Le mot disque est employé, aussi bien en géométrie que dans la vie courante, pour désigner une...), taille de la mémoire, mouvements du pointeur de la souris (Le terme souris est un nom vernaculaire ambigu qui peut désigner, pour les francophones, avant...)...) et à faire passer (Le genre Passer a été créé par le zoologiste français Mathurin Jacques...) le résultat dans une fonction de hachage (On nomme fonction de hachage une fonction particulière qui, à partir d'une donnée...) cryptographique comme MD5 ou SHA-1. Ce principe est utilisé par Yarrow et Fortuna qui ne génèrent un nombre que lorsque l'entropie (En thermodynamique, l'entropie est une fonction d'état introduite en 1865 par Rudolf Clausius...) est suffisante.

Domaines d'application

Les générateurs pseudo-aléatoires ont, à travers le temps, acquis une grande importance dans divers domaines, allant du médical à la sécurisation, et se sont montrés être d’une grande efficacité quant à leurs apports dans ces domaines.

Confidentialité des échanges sur les réseaux sans fils

L’échange par réseaux sans fil pose de nombreux problèmes concernant la confidentialité des éléments échangés. Ceci dit, il faut alors un mécanisme qui peut conserver le mieux possible cette confidentialité, ce mécanisme est alors le WEP pour Wired Equivalent Privacy. Le principe consiste à définir une clé chiffrée sur une longueur allant de 40 à 128 bits. Ensuite, la clé est déclarée au niveau du point (Graphie) d’accès et du client (Le mot client a plusieurs acceptations :). Le but de la clé est de créer un nombre pseudo aléatoire d’une longueur égale à celle de la trame (Le mot trame peut désigner :) de transmission. Le nombre pseudo aléatoire ainsi généré sert à chiffrer la transmission, et alors à assurer la confidentialité de cette dernière.

Toutefois, le WEP n’assure malheureusement pas une sécurité optimale, les compagnies Fluhrer et Shamir ont montré que la génération de la chaîne (Le mot chaîne peut avoir plusieurs significations :) pseudo aléatoire rend possible la découverte de la clé de session en stockant 100 Mo à 1 Go de trafic créé intentionnellement. Notons aussi que 24 bits de la clé sont dédiés à l’initialisation, ce qui veut dire que chiffrer à 128 bits est de loin meilleur que de chiffrer à 64 bits dans la mesure où chiffrer à 128 bits offre une possibilité réelle de chiffrer de 104 bits tandis que chiffrer a 64 bits n’en offre que 40 bits.

Sécurisation des applications web

Les applications WEB qui ont pour utilisateurs les navigateurs WEB ont un système qui sert à protéger leurs clients par la création de sessions. Les sessions sont des espaces de travail qui ont un espace de stockage d’informations connu, elles sont aussi privées et appartiennent à un utilisateur particulier dûment authentifié.

Néanmoins, ces sessions ne présentent pas toujours le niveau de sécurité souhaité. C’est ici qu’interviennent les nombres pseudo aléatoires. L’exemple le plus connu est celui d’attaque par session de type prédiction (méthode de détourner ou de personnifier un utilisateur WEB, elle s’accomplit par la déduction ou l'estimation de la valeur unique qui identifie la session associée). Pour éviter ce genre d’attaques, il est devenu courant d’utiliser un gestionnaire d’applications WEB capable de générer des identifiants qu’on ne peut pas prévoir. Il n’y a plus à chercher, car les applications de génération de nombres pseudo aléatoires ont été suffisamment développées pour ce faire.

Système de chiffrement

La cryptanalyse est une discipline récente, et signe un grand niveau de fiabilité (Un système est fiable lorsque la probabilité de remplir sa mission sur une durée...) quant aux méthodes de chiffrement qu’elle utilise, notamment le chiffrement à flot. Ce denier consiste à additionner bit à bit au message (La théorie de l'information fut mise au point pour déterminer mathématiquement le taux...) clair une suite binaire pseudo aléatoire de même longueur appelée suite chiffrante. Ce procédé est reconnu pour sa rapidité et sa compétitivité vis-à-vis des autres procédés dans la mesure où il est peu sensible aux erreurs introduites lors de la transmission. Des registres à décalage avec rétroaction linéaire font souvent partie des générateurs pseudo aléatoires utilisés pour produire les suites chiffrantes.

Domaine biomédical

Une application importante au niveau biomédical concerne l’amélioration de la modélisation du dépôt de dose dans le corps et aussi pour accélérer le calcul de traitement. En effet, sur les grilles de calcul, il est impératif que chaque processus de calcul puisse disposer d’une sous séquence aléatoire issue d’une séquence globale de nombres aléatoires à générer. L’un des fruits des recherches menées à ce sujet, est la plate-forme de simulation Monte-Carlo GATE, qui est un logiciel (En informatique, un logiciel est un ensemble d'informations relatives à des traitements...) de calcul de dépôt de dose sur plusieurs grappes, et qui a permis de mettre en évidence des facteurs d’accélération de l’ordre de 30 du temps de calcul en comparaison avec une utilisation en milieu hospitalier.

Une application originale : le GPS

Les codes pseudo-aléatoires connaissent une application originale dans le cadre du système de localisation par satellites GPS. Ils y sont en effet utilisés non pas en fonction de leur prévisibilité vis-à-vis d’une analyse extérieure pour protéger des données, mais parce qu’ils présentent une séquence connue, facile à calculer, et qui n’a aucune similitude avec les séquences obtenues en changeant de graine.

Ces caractéristiques sont utiles aux GPS à cause de l’utilisation qui en est faite : Le but est de mesurer une distance entre deux équipements, en l’occurrence un satellite (Satellite peut faire référence à :) de la constellation (Une constellation est un ensemble d'étoiles dont les projections sur la voûte...) GPS et un récepteur.

Cette mesure est réalisée en générant une séquence pseudo-aléatoire sur chacun des équipements, que l’on supposera synchronisés, et générant la séquence à la même vitesse. La séquence du satellite (Satellite peut faire référence à :) est alors modulée et transmise au récepteur, qui la compare a sa propre séquence. Il y a alors un décalage entre les deux chaînes, et ce décalage correspond au temps de propagation de l’information du satellite au récepteur. Il suffit alors de mesurer ce décalage, de le multiplier par la vitesse des ondes (Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible...) électromagnétiques dans l’air et on obtient la distance recherchée.

Ce principe est toutefois contrarié dans la réalité par de multiples facteurs qui conditionnent le choix du générateur pseudo-aléatoire à utiliser :

• Les séquences générées par les codes pseudo-aléatoires ne sont pas infinies et se répètent périodiquement, la période dépendant du code utilisé et de la machine sur laquelle il est implanté. Ce " défaut " entraîne une ambiguïté sur la distance mesurée par le récepteur : le décalage mesuré est de t, mais il peut aussi être de t+T (où T est la période de la séquence), de t-T, ou de tout nombre entier de périodes. Il est à priori impossible de lever cette ambiguïté sans traitement informatique qui relie la mesure de distance réalisée a la position du récepteur estimée précédemment. C’est pourquoi une caractéristique importante des codes pseudo-aléatoires utilisés dans le système GPS est leur période, qui doit être la plus longue possible : l’un des codes utilisés, appelé code P, possède une longueur d’onde supérieure au diamètre (Dans un cercle ou une sphère, le diamètre est un segment de droite passant par le centre...) de la terre (La Terre est la troisième planète du Système solaire par ordre de distance...), ce qui fait disparaître de problème de l’ambiguïté.

• La vitesse de génération du code par les équipements conditionne la précision de la mesure de distance. En effet, la précision ne pourra jamais être plus grande que la distance élémentaire obtenue en multipliant le temps nécessaire a calculer ou émettre un bit par la vitesse de la lumière (La vitesse de la lumière dans le vide, notée c (pour...). En d’autres termes, on ne peut pas être plus précis que la distance parcourue par le signal ( Termes généraux Un signal est un message simplifié et généralement codé. Il existe...) du satellite pendant l’émission d’un bit du code. Il est donc primordial de posséder un code généré extrêmement rapidement, et dont la formule de calcul soit la plus simple possible. À titre d’exemple, pour obtenir une précision idéale de l’ordre du mètre (Le mètre (symbole m, du grec metron, mesure) est l'unité de base de longueur du...), il faudrait générer un bit toutes les 3 nanosecondes.

• La méthode de mesure du décalage entre les deux codes est réalisée par une fonction de corrélation. La première caractéristique que cela impose au code est d’avoir une autocorrélation aussi proche que possible d’un pic de Dirac : si l’autocorrélation du code est importante quand il y a décalage de phase (Le mot phase peut avoir plusieurs significations, il employé dans plusieurs domaines et...), il deviendra impossible de mesurer le décalage car il y aura ambiguïté entre deux possibles. De même, si entre deux satellites la corrélation des codes n’est pas faible, leurs signaux se perturberont mutuellement et cela rendra la mesure difficile voire irréalisable.

L’ensemble de ces facteurs ont conduit les constructeurs du système GPS à utiliser les codes de Gold. Ces codes, basés sur la combinaison (Une combinaison peut être :) de deux séquences binaires, présentent des caractéristiques intéressantes pour le GPS : ils sont relativement faciles a calculer, et possèdent des périodes appropriées. Le point fort des codes de Gold est leur excellente réponse au 3ème critère : la corrélation de deux codes est faible, que ce soient deux codes décalés ou différents, et le seul cas ou la corrélation est forte est celui de deux mêmes codes en phase. De ce fait, ils sont très utilisés en télécommunications (Les télécommunications sont aujourd’hui définies comme la transmission à distance...) pour réaliser le multiplexage (Le multiplexage est une technique qui consiste à faire passer deux ou plusieurs informations à...) par codes ou CDMA.