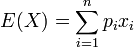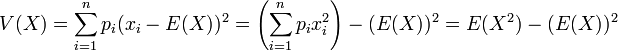Variables aléatoires élémentaires - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
La notion de variable aléatoire réelle est utilisée dès que le résultat d’une expérience aléatoire est quantifiable. Elle est née de considération sur les jeux où, à chaque jeu, pouvait être associé un gain (= somme empochée - mise). La question était de savoir comment répartir de façon juste les mises en cas d’arrêt forcé en cours de partie. Blaise Pascal contribua grandement à la fonder.
On nomme variable aléatoire réelle une application X d’un univers Ω muni d’une probabilité p vers R. Cette application crée un nouvel univers X(Ω) sur lequel on peut construire une probabilité issue de p. Cette probabilité s’appelle loi de probabilité de X. Il arrive souvent que l’on oublie l’univers Ω pour ne s’intéresser qu’à l’univers X(Ω). En français, retenons essentiellement qu’une variable aléatoire se présente comme une fonction.
Cas des variables aléatoires définies sur un univers Ω fini.
Si l’univers Ω est fini, alors l’univers X(Ω) est fini. X(Ω) = {x1, x2, ..., xn}.
Loi de probabilité
Attention : l’approche fréquentiste utilisée dans cette section ne résume pas à elle seule la notion de probabilité. Elle ne fait qu’en fournir un exemple. Nombre de probabilités sont associées à des événements où aucune notion de fréquence n’intervient.
La loi de probabilité peut se construire de la manière suivante : pX(xi) = p(X = xi). = pi
Exemple: En lançant deux dés, on crée un univers Ω de 36 éléments formé de couples d’entiers de 1 à 6. Sur cet univers, on définit une équiprobabilité (les lancers des 2 dés étant deux expériences indépendantes). Si l’on ne s’intéresse qu’à la somme des deux dés, il faut créer une variable aléatoire X qui, à chaque couple, associe leur somme.
L’univers X(Ω) est donc {2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12}. Cet univers contient 11 éléments, mais il n’est pas adéquat d’y définir une équiprobabilité.
- pX(7) = p(X = 7) = p({(1 , 6)}) + p({(2, 5)}) + p({(3 , 4)}) + p({(4 , 3)}) + p({(5 , 2)}) + p({(6 , 1)}) = 6/36 = 1/6
- pX(2) = p(X = 2) = p({1 , 1}) = 1/36
On peut ainsi créer une loi de probabilité sur X(Ω)
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| pi | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Espérance, variance et écart type
La présentation de la loi de probabilité sous forme d’un tableau ressemblant au tableau des fréquences d’une série statistique quantitative discrète et la loi des grands nombres qui stipule que les deux tableaux coïncident si on renouvelle un grand nombre de fois l’expérience, pousse à définir aussi pour X la moyenne, la variance et l’écart type.
La moyenne de la série statistique sera appelé espérance dans le cas d’une variable aléatoire. Ce terme provient sans doute de l'utilité des premières variables aléatoires dans les calculs statistiques sur les gains des jeux de hasard. L’espérance du gain correspond alors à la moyenne des gains au cours de nombreuses parties.
La variance s’écrit alors, par analogie avec la formule de la variance avec fréquences:
L’écart type reste toujours la racine carrée de la variance :
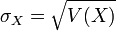
Fonction de répartition
La fonction de répartition d'une variable aléatoire X est la fonction F définie sur R par F(x) = p(X ≤ x).
Dans le cas d’une variable discrète, c’est une fonction en escalier. En effet :
- si x < x1 alors F(x) = 0.
- si
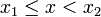
- si
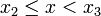
- ...
- si
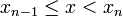
- si
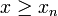
Lois célèbres
Outre l’équiprobabilité, on peut rencontrer aussi
Variables aléatoires à densité
Il arrive que l’univers Ω soit infini et que l’univers X(Ω) soit aussi infini. Le calcul des pX(x) pour tout x de X(Ω) n’est souvent pas suffisant pour calculer la probabilité d’un événement et il est même fréquent que ces pX(x) soient tous nuls. Il est alors nécessaire de calculer directement pX([a ; b]).
Densité de probabilité
On dit que X est une variable aléatoire de densité f si la probabilité de l’événement " a ≤ X ≤ b " vaut
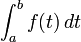
On peut remarquer que p([a ; a]) = 0, donc que p(]a ; b]) = p([a ; b]) ce qui explique la liberté prise dans ce cas avec les inégalités larges ou strictes.
De l'histogramme à la densité de probabilité
En renouvelant 10000 fois l'expérience X, on crée une série statistique continue. On peut alors ranger les différentes valeurs obtenues dans des classes de même amplitude et tracer l'histogramme des fréquences. L’aire du rectangle de base [xi, xi+1] représente la fréquence de la classe [xi, xi+1]. Cet histogramme dessine une fonction en escalier.
L'aire sous la courbe entre xi et xj représente la fréquence de la classe [xi , xj]. Or la loi des grands nombres nous dit que cette fréquence est une bonne approximation de p([xi , xj]). En multipliant les expériences et en affinant les classes, la fonction en escaliers se rapproche d'une fonction souvent continue, l'aire sous cette courbe sur l'intervalle [a ; b] est alors un bon représentant de la probabilité de l'intervalle [a ; b]. Cette fonction s'appelle la densité de probabilité de la variable X.
On prend souvent l’habitude de tracer cette densité de probabilité pour mieux visualiser la loi de probabilité associée en regardant l’aire sous la courbe entre les valeurs qui nous intéressent.
Loi uniforme
Le cas le plus simple de loi à densité est la loi uniforme. Les valeurs de X se répartissent uniformément sur un intervalle [a ; b]. L'histogramme que l'on pourrait dessiner serait une succession de rectangles de même hauteur. La densité de probabilité est donc une fonction constante k. L'aire sous la courbe sur l'intervalle [a ; b] vaut alors k(b - a). Or cette aire doit valoir 1, donc k = 1/(b-a).
La probabilité de l'intervalle [c ; d] (inclus dans [a ; b]) est alors k(d - c) =
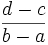
Autres lois
On rencontre aussi
- La loi exponentielle dite aussi de durée de vie sans vieillissement
- La loi normale, dite aussi loi de Laplace-Gauss, ou loi normale gaussienne, ou loi de Gauss.
Ces deux lois sont également celles de distributions d’entropie maximale sous contrainte, la première quand la seule contrainte imposée est la moyenne, la seconde quand sont imposées une moyenne et une variance. Cette caractéristique montre leur caractère général : de toutes les distributions obéissant à ces contraintes, ce sont les moins prévenues, les moins arbitraires, les plus générales, bref, les plus neutres : celles qui n’introduisent pas d’information supplémentaire (et donc arbitraire) par rapport à ce qui est donné.
Espérance, variance et écart type
La méthode d’approximation d’une intégrale par la méthode des rectangles conduit à définir l’espérance et la variance comme des intégrales issues du passage à la limite des sommes définissant moyenne et variance dans le cas d’une variable statistique continue.
De la moyenne de la série statistique, on passe à l’espérance de X par la formule.
-
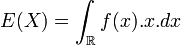
La variance s’écrit alors, par analogie avec la formule de la variance avec fréquences:
-
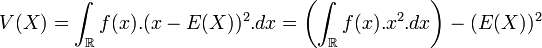
L’écart type reste toujours la racine carrée de la variance :
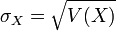
Fonction de répartition
La fonction de répartition est la fonction F définie sur R par F(x) = p(X ≤ x).
Dans le cas d’une variable à densité, c’est la primitive de f dont la limite en + ∞ est 1.
En effet
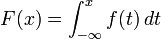
Médiane
Si la fonction de répartition F est continue et strictement croissante, elle définit une bijection de R sur ]0 ; 1[. Il existe donc alors une valeur unique M telle que F(M) = 1/2. Cette valeur s'appelle la médiane de la variable aléatoire X. Elle vérifie p(X ≤ M) = p(X > M) = 0,5.
Cas des variables aléatoires ayant une infinité dénombrable de valeurs
Ce cas sort du cadre des mathématiques élémentaires, mais mérite cependant d'être évoqué. Ces variables font le lien entre les variables discrètes prenant n valeurs, n grand, et les variables continues.
Il est possible de définir pX(xi) pour tout i de N.
Les lois les plus connues de variables aléatoires à valeurs dans N sont :