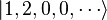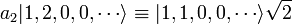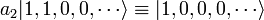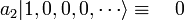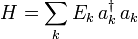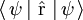Théorie quantique des champs - Définition

Articles de physique quantique |
| Théorie quantique |
| Électrodynamique quantique |
| Mécanique quantique |
| Théorie des champs |
| Modèle standard |
| Statistiques quantique |
| Bose-Einstein |
| Fermi-Dirac |
| Maxwell-Boltzmann |
| Physiciens |
| Bohr - de Broglie |
| Bose - Einstein |
| Fermi - Dirac |
| Heisenberg - Pauli |
| Schrödinger - Feynman |
La théorie quantique des champs est l'application des concepts de la physique quantique aux champs. Issue de la mécanique quantique relativiste, dont l'interprétation comme théorie décrivant une seule particule s'était avérée incohérente, la théorie quantique des champs fournit un cadre conceptuel largement utilisé en physique des particules, en physique de la matière condensée, et en physique statistique.
La première théorie quantique des champs à avoir vu le jour, connue sous le nom d'électrodynamique quantique, est aujourd'hui une des théories physique ayant le plus beau succès dans sa confrontation aux résultats expérimentaux dans le cadre du modèle standard notamment grâce à la mesure de haute précision de la constante de structure fine.
Historique
La théorie quantique des champs naît en 1927 avec l'article fondateur de l'électrodynamique quantique par Dirac : " La théorie quantique de l'émission et de l'absorption du rayonnement ". Le formalisme est ensuite développé et discuté dans les années 1930 par les théoriciens, ceux-ci se heurtant à un problème récurrent : l'apparition systématique d'infinis lors des calculs de grandeurs physiques censées être mesurables et finies. Cette difficulté ne fut entièrement surmontée qu'en 1948 avec l'invention d'une procédure systématique, la renormalisation, due principalement au japonais Tomonaga et aux américains Schwinger et Feynman.
Les succès de l'électrodynamique quantique, théorie de jauge abélienne, a conduit les théoriciens des années 1960 et 1970 à appliquer les concepts de la théorie quantiques des champs aux théories de jauge non abéliennes, donnant finalement naissance à l'actuel modèle standard de la physique des particules.
Par ailleurs, Kadanoff a introduit à la fin des années 1960 l'idée que les transitions de phases décrites par la physique statistique présentaient des propriétés d'universalité et d'invariance d'échelles. Wilson eut alors l'idée d'appliquer les méthodes de renormalisation de la théorie quantique des champs à la description des phénomènes critiques. [1]
Champs quantiques
La façon dont la théorie des champs fut introduite par Dirac à partir des particules élémentaires est connue pour des raisons historiques sous l'appelation de seconde quantification.
Il faut mentionner deux sources de confusions:
- les champs ne sont pas liés à la dualité onde corpuscule.
les particules élémentaires possèdent déjà cette dualité dans l'acceptation du terme de la mécanique classique. Ce que l'on entend par champ est un concept qui permet la création ou l'annihilation de particules en tout point de l'espace. Comme tout système quantique, un champ quantique a un hamiltonien et obéit à l'équation de Schrödinger :
(en théorie des champs, le formalisme lagrangien est plus facile à utiliser que son équivalent le hamiltonien)
- avec la seconde quantification, l'indiscernabilité des particules s'exprime en termes de nombre d'occupation.
Supposons que N = 3, avec une particule dans l'état φ1 et deux dans l'état φ2. la façon d'écrire la fonction d'onde est:
alors qu'avec la seconde quantification, cette fonction est simplement
Quoique la différence soit minime, la deuxième permet d'exprimer facilement des opérateurs création et annihilation , qui rajoutent ou enlèvent des particules à l'état.
Ces opérateurs création et annihilation très similaires à ceux définis dans oscillateur harmonique quantique, qui en mécanique quantique crée ou détruit des quanta d'énergie.
Ces operateurs créent et font disparaître des particules dans un état quantique donné.
Par exemple, l'operateur a2 a l'effet suivant:
(Le facteur √2 normalise la fonction d'onde.)
Enfin, il faut introduire " les opérateurs de champ " de création ou d'annihilation d'une particule en un point de l'espace.
De même que pour une seule particule la fonction d'onde s'exprime avec son moment cinétique, de même les opérateurs de champ peuvent s'exprimer à l'aide des transformées de Fourier.
Par exemple:
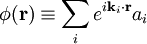
Les Hamiltoniens, en physique des particules sont écrits
comme une somme d'opérateurs création et annihilation de champ.
Cela exprime un champ de bosons libres où Ek est l'énergie cinétique. En fait, cet Hamiltonien est utilisé pour décrire des phonons.
Champ & particule ?
Introduction : le problème de la localisation
L'expérimentateur qui enregistre un " clic " dans son détecteur aimerait relier cet évènement, qu'il interpète comme la détection d'une " particule " relativement bien localisée dans l'espace (et dans le temps), au champ quantique et à ses excitations : c'est le problème de la localisation. Ce problème, qui admet une réponse simple en mécanique quantique non-relativiste, est hautement non-trivial en théorie quantique relativiste.
Localisation en mécanique quantique non-relativiste
Dans le cadre de la mécanique quantique non-relativiste, on dispose d'un opérateur position
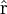
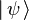
- l'écart quadratique moyen (dispersion) Δr autour de cette position moyenne est défini par :
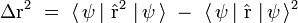
La particule quantique est d'autant mieux localisée en position que cette dispersion est petite ; la mécanique quantique n'interdit d'ailleurs pas de la prendre nulle, auquel cas la localisation spatiale est parfaitement réalisée. Bien évidemment, il y a alors une dispersion maximale en quantité de mouvement pour satisfaire les inégalités de Heisenberg.
Opérateur position en mécanique quantique relativiste ?
En mécanique quantique relativiste, les transformations de Lorentz mélangent espace et temps : si le vecteur position classique était associé à un opérateur position quantique "à la Heisenberg", il devrait aussi exister un opérateur temps.
Or, un vieil argument de Pauli suggère[2] qu'il n'existe pas d'opérateur temps hermitien en mécanique quantique. En effet, en mécanique hamiltonienne, temps et énergie sont conjugués : l'opérateur hamiltonien est le "générateur infinitésimal" des translations dans le temps (par le théorème de Noether). Par analogie avec le couple position/impulsion satisfaisant
![[\hat{\mathrm{x}}^i, \, \hat{\mathrm{p}}_j ] = i \ \hbar \ \hat{\mathrm{\delta}}_j^i](https://static.techno-science.net/illustration/Definitions/autres/8/8034e312ecd183b6380fd1cf87094c14_2be64c38d54bfd766fb21f23b3ad9178.png)
![[\hat{\mathrm{H}},\hat{\mathrm{t}}] = (\pm) \ i \ \hbar \ \hat{\mathrm{1}}](https://static.techno-science.net/illustration/Definitions/autres/8/8cf4ff3a925a41bb3f86a18ebb8082ea_0505cbe34bf63c6499d31332472d534c.png)

La solution consiste à abandonner la notion d'opérateur position, et donc à passer aux champs, fonctions définies sur l'espace-temps.
Système élémentaire au sens de Wigner
Localisation douce : l'opérateur position de Newton-Wigner (1949)
En 1949, Newton et Wigner[3] ont malgré tout réussi à construire un nouvel "opérateur position" pour les particules massives (de spin arbitraire). Modulo quelques hypothèses générales "raisonnables", il sont arrivés à un opérateur non-local dans l'espace physique. Les "états localisés" associés à cet opérateur ne sont pas des distributions de Dirac. L'état localisé autour de l'origine possède à grande distance une décroissance exponentielle avec une échelle caractéristique égale à la longueur d'onde Compton de la particule massive. Il est donc impossible de localiser une particule, ni ponctuellement, ni " strictement " (au sens de : dans un compact). De plus, ces états localisés ne sont pas invariants par transformation de Lorentz : une particule localisée dans un référentiel ne l'est pas nécessairement dans un autre. Enfin, la construction de Newton-Wigner s'étend aux particules de masse nulle de spin 0 (décrites par l'équation de Klein-Gordon) et de spin 1/2 (décrites par l'équation de Dirac), mais hélas pas au photon, de spin 1.
Impossibilité d'une localisation stricte ?
Le théorème de Malament (1996)
Théorème de Malament[4]
Le théorème de Clifton et Halvorson (2002)
Théorème de Clifton et Halvorson[5]
Notes
- ↑ référence, citation ou lien
- ↑ Eric Galapon a récemment remis en cause la validité du raisonnement de Pauli ; cf. e.g. : quant-ph/9908033 ; quant-ph/0111061 ; quant-ph/0303106.
- ↑ T. D. Newton and E. P. Wigner ; Localized States for Elementary Systems, Review of Modern Physics 21 (1949), 400 - 406. pdf.
- ↑ David B Malament ; In Defense of Dogma -- Why There Cannot Be a Relativistic Quantum Mechanical Theory of (Localizable) Particles, dans : R Clifton (éditeur) ; Perspectives on Quantum Reality, Kluwer (1996). pdf.
- ↑ Hans Halvorson & Rob Clifton ; No place for particles in relativistic quantum theories ?, Philosophy of Science 69 (2002) 1-28. ArXiv :quant-ph/0103041.
Bibliographie
Textes en français
- Laverne, Alain ; Rayonnement quantique, cours donné en 1994 par Alain Laverne (Université Paris 7) sur la quantification du rayonnement électromagnétique et le concept de photon. 240 pages.
- Bell, John S. ; Théorie quantique des champs expérimentale, traduction française par Alain Laverne (Université Paris 7) d'un cours d'introduction donné en 1977 par John S. Bell (Physique Théorique, CERN) aux physiciens expérimentateurs. 41 pages.
- Delamotte, Bertrand ; Un soupçon de théorie des groupes : groupe des rotations & groupe de Poincaré , cours d'introduction pour physiciens (prolégomènes à un cours de théorie quantique des champs) donné en 1995 par Bertrand Delamotte (Laboratoire de Physique Théorique et Hautes Energies, Université Paris 7) au DEA "Champs, Particules, Matières" . 127 pages.
- Laloë, Franck ; Cours sur les symétries, cours pour physiciens (prolégomènes à un cours de théorie quantique des champs) donné par Franck Laloë (Laboratoire de Physique Atomique, ENS Ulm, Paris) au DEA de Physique Quantique.
- Zinn-Justin, Jean ; Des infinis de la mécanique quantique relativiste au groupe de renormalisation, texte d'une conférence donnée par Jean Zinn-Justin (Service de Physique Théorique du CEA) lors de la 5me rencontre "Physique et Interrogations Fondamentales" (PIF V) intitulée : L'élémentaire et le complexe. Universel et singulier (III) (27 octobre 1999, Collège de France, Paris). Publié par : Michel Crozon & Yves Sacquin (éditeurs), EDP Sciences (2001).
- Le Bellac, Michel ; Des phénomènes critiques aux champs de jauge - Une introduction aux méthodes et aux applications de la théorie quantique des champs, InterEditions/Editions du CNRS (1988), ISBN 2-86883-359-4. Réédité par EDP Sciences.
Textes en anglais
- Wilczek, Frank ; Quantum Field Theory, Review of Modern Physics 71 (1999) S85-S95. Article de revue écrit par un Maître de la QCD, prix Nobel 2003. ArXiV : hep-th/9803075
- Zee, Anthony ; Quantum Field Theory in a Nutshell, Princeton University Press (2003), ISBN 0-691-01019-6. La meilleure introduction à la théorie quantique des champs. Pédagogique et même divertissant. Aspects de la théorie de la matière condensée comme de celle des hautes énergies.
- Ryder, Lewis H. ; Quantum Field Theory , Cambridge University Press (1985), ISBN 0-521-33859-X Ouvrage remarquable, qui complète à merveille le précédent pour la théorie quantique des champs appliquée à la physique des particules.
- Peskin, M and Schroeder, D. ;An Introduction to Quantum Field Theory (Westview Press, 1995), ISBN 0201503972. Pas à pas détaillé.
- Weinberg, Steven ; The Quantum Theory of Fields, Cambridge University Press (1995). Traité monumental en 3 volumes par un expert du domaine, prix Nobel 1979.
- Loudon, Rodney ; The Quantum Theory of Light (Oxford University Press, 1983), ISBN 0198511558
- Siegel, Warren ; Fields. ArXiV : arXiv:hep-th/9912205). Atypique.
- 't Hooft, Gerard ; The Conceptual Basis of Quantum Field Theory, Handbook of the Philosophy of Science, Elsevier (à paraître). Article de revue écrit par un Maître des théories de jauge, prix Nobel 1999. pdf.
- Srednicki, Mark ; Quantum Field Theory
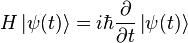
![\frac{1}{\sqrt{3}} \left[ \phi_1(r_1) \phi_2(r_2) \phi_2(r_3) + \phi_2(r_1) \phi_1(r_2) \phi_2(r_3) + \phi_2(r_1) \phi_2(r_2) \phi_1(r_3) \right]](https://static.techno-science.net/illustration/Definitions/autres/8/833350313ed2b1360d056ca0cb7d768c_d478eca41451c7a239d16bf9fc747132.png)