Norme (arithmétique) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques la norme est une notion utilisée en théorie de Galois ou en théorie algébrique des nombres.
La théorie classique de Galois étudie des extensions finies L d'un corps K un autre corps commutatif. L'ensemble L contient K (ou, ce qui revient au même, il existe un morphisme de corps injectif de K dans L), L est commutatif et L, considéré comme un espace vectoriel sur le corps K est de dimension finie. Une première définition de la norme est l'application qui à un élément l de L associe le déterminant de la fonction multiplication par l.
En arithmétique, la norme relative est une application d'un sur-corps L vers un sous-corps K d'une extension. Cette application intervient de façon cruciale dans la théorie des corps de classes : les sous-extensions abéliennes d'une extension donnée sont essentiellement en correspondance avec des groupes de normes, c'est-à-dire l'image dans le sous-corps par la norme de certains groupes du sur-corps.
Cette notion s'étend en une notion de norme d'un idéal, définie pour les idéaux premiers comme le cardinal du corps résiduel, puis par multiplicativité, pour les idéaux composés. La norme d'un idéal principal est alors égale à la norme relative sur Q, l'ensemble des nombres rationnels, d'un générateur de cet idéal. La démonstration de la finitude du groupe des classes utilise des propriétés de majoration de la norme des idéaux dans une classe donnée.
Définitions
Soit K un corps commutatif, L une extension finie et l un élément de L. Une première définition est la suivante :
-
- La norme relative de l'élément l dans K est le déterminant de l'endomorphisme du K espace vectoriel L qui à x associe l.x. Cette norme est généralement notée NL/K(l).
Il existe une définition plus restrictive et équivalente si les conditions d'existence sont remplies :
-
- Si l'extension L est galoisienne, la norme relative d'un élément l de L est le produit des images d'une racine du polynôme minimal par les différents automorphismes du groupe de Galois.
La norme d'un nombre algébrique peut être définie sans référence à la donnée d'une extension L, on parle alors de norme et non plus de norme relative.
-
- La norme d'un nombre α algébrique dans K est égale au coefficient constant de son polynôme minimal si le polynôme est séparable. Une telle norme est parfois notée N(α).
Cette définition s'applique encore si le nombre est un entier algébrique, la norme est alors entière. Elle se généralise aux idéaux d'un anneau d'entiers algébriques :
-
- La norme d'un idéal M de la fermeture algébrique OL de L est l'ordre de l'anneau quotient M/OL si le corps K est celui des nombres rationnels.
Applications
Les normes permettent parfois d'établir le caractère euclidien de certains anneaux d'entiers. Tel est le cas pour les entiers de Gauss, d'Eisenstein et de Dirichlet.
Dans le cas plus général des corps quadratiques la norme aide à élucider la structure de l'anneau pour permettre par exemple de résoudre l'équation x2 + 5.y2 = n où n est un entier.
D'une manière encore plus générale, la norme est utilisée pour établir les résultats clé de la théorie algébrique des nombres, comme la structure des idéaux fractionnaires ou celle du groupe des classes d'idéaux.
Propriétés
Théorie de Galois
Si les trois définitions semblent a priori éloignées les unes des autres, la réalité est différente :
-
- Si une extension finie L est galoisienne, le déterminant de l'application multiplication par l, où l est un élément de L est égal au produit des images d'une racine du polynôme minimal par les différents automorphismes du groupe de Galois.
L'article polynôme minimal d'un nombre algébrique montre que si σ1, σ2, ..., σd désigne les différents éléments du groupe de Galois, d étant la dimension de L en tant que K espace vectoriel et χ[X] le polynôme caractéristique, l'égalité suivante est vérifiée :
![\chi[X] =\prod_{i=1}^d \Big(\sigma_i(m) - X\Big)\quad \text{et}\quad \mathcal N_{\mathbb L/\mathbb K} (l) = \prod_{i=1}^d \sigma_i(m)](https://static.techno-science.net/illustration/Definitions/autres/2/20146bced12c0a2cf162db5e41de343b_e7f846749e9f6c27caf3bc2b4646e5c3.png)
Le déterminant est égal au monôme constant du polynôme caractéristique, correspondant bien au produit des σi(m) pour i décrivant l'intervalle de borne 1 et d.
La définition d'une norme relative à une extension et d'une norme est un peu différente. Il suffit de considérer un élément k de K pour s'en rendre compte, sa norme relative est égal à kd et sa norme à k.
-
- Soit l un élément de L et n la dimension de l'espace vectoriel L sur le corps de rupture K[l]. Si N(l) désigne la norme de l et NL/K(l) sa norme relative, alors :
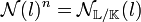
Ce résultat provient de l'égalité suivante, si P(X) désigne le polynôme minimal de l, démontrée dans l'article polynôme minimal d'un nombre algébrique :
![\chi[X] = (-1)^n P^n[X]\;](https://static.techno-science.net/illustration/Definitions/autres/a/a4a726d83577cff13cc660ec9be3a8c5_9fa6e34f46e091476d2e1199a9ba7ca3.png)
Une propriété est vérifiée pour la norme relative :
-
- Soit l1 et l2 deux éléments de L, le produit des normes relatives de l1 et l2 est égal à la norme relative du produit l1.l2.
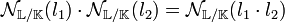
Cette propriété est la conséquence directe du fait que le produit de deux déterminants est égal au déterminant des produits. L'égalité n'est en général pas vraie pour les normes. Il n'existe en effet aucune raison pour que les corps de ruptures aient même dimension.
Théorie algébrique des nombres
Ici, K est une extension finie des nombres rationnels et L une extension finie de K. On considère deux anneaux OK et OL fermeture intégrale des corps K et L. Ce sont des anneaux de Dedekind. La norme considérée est la norme relative. Un cas particulier simple est étudié dans l'article Entier quadratique.
-
- La norme relative de L sur K d'un entier α de OL est un entier de OK.
Dire que α, un élément de L est entier sur K revient à dire que son polynôme minimal est à coefficients dans les entiers algébriques de OK. Son polynôme caractéristique, puissance du polynôme minimal est aussi à coefficients dans les entiers de OK, ce qui montre le caractère intégrale de la norme.
La norme relative dispose d'une propriété remarquable si K est égal à Q le corps des rationnels :
-
- La valeur absolue de la norme relative d'un entier algébrique α de L sur Q est égale au cardinal de l'anneau quotient OL/ αOL.
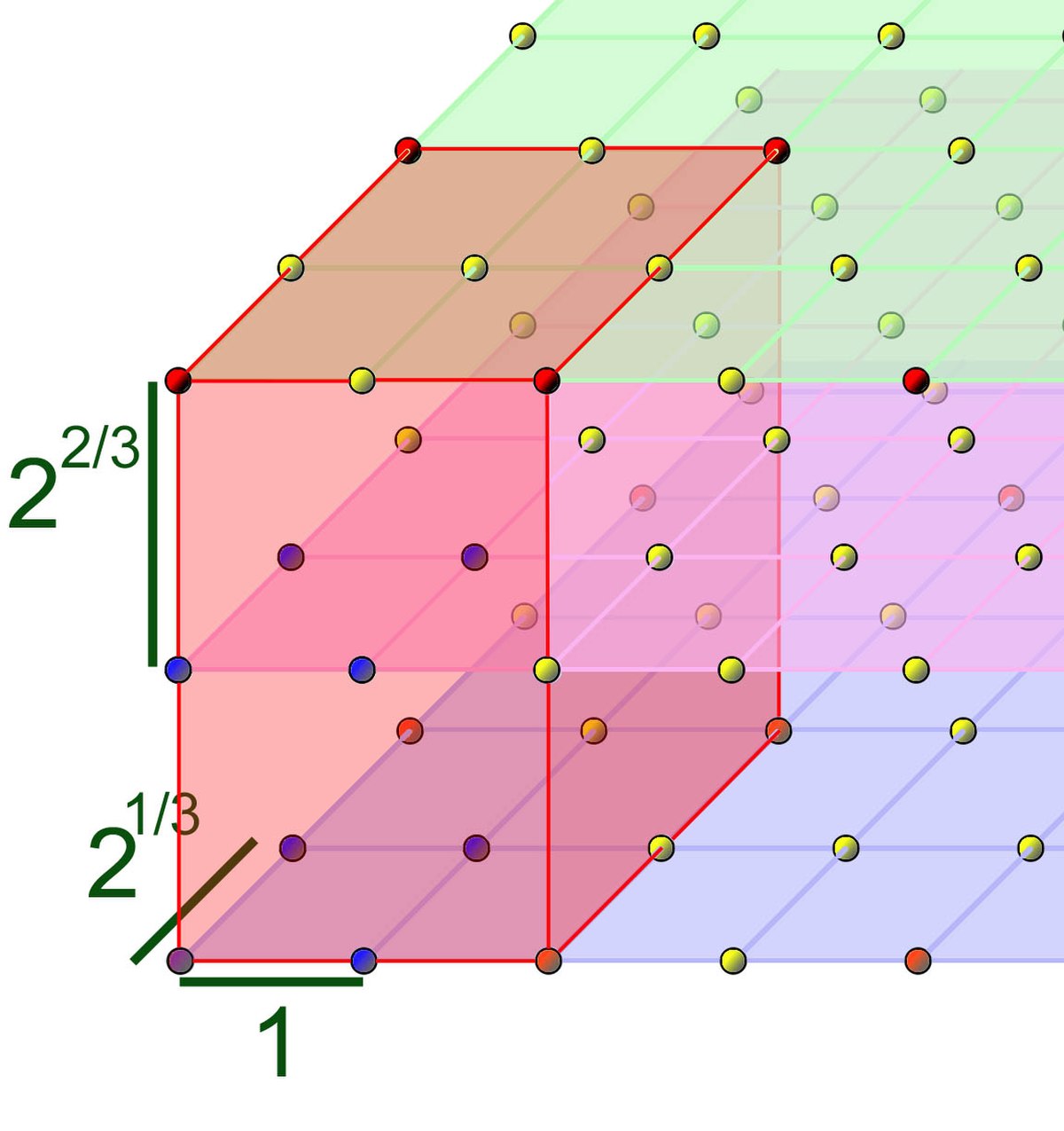
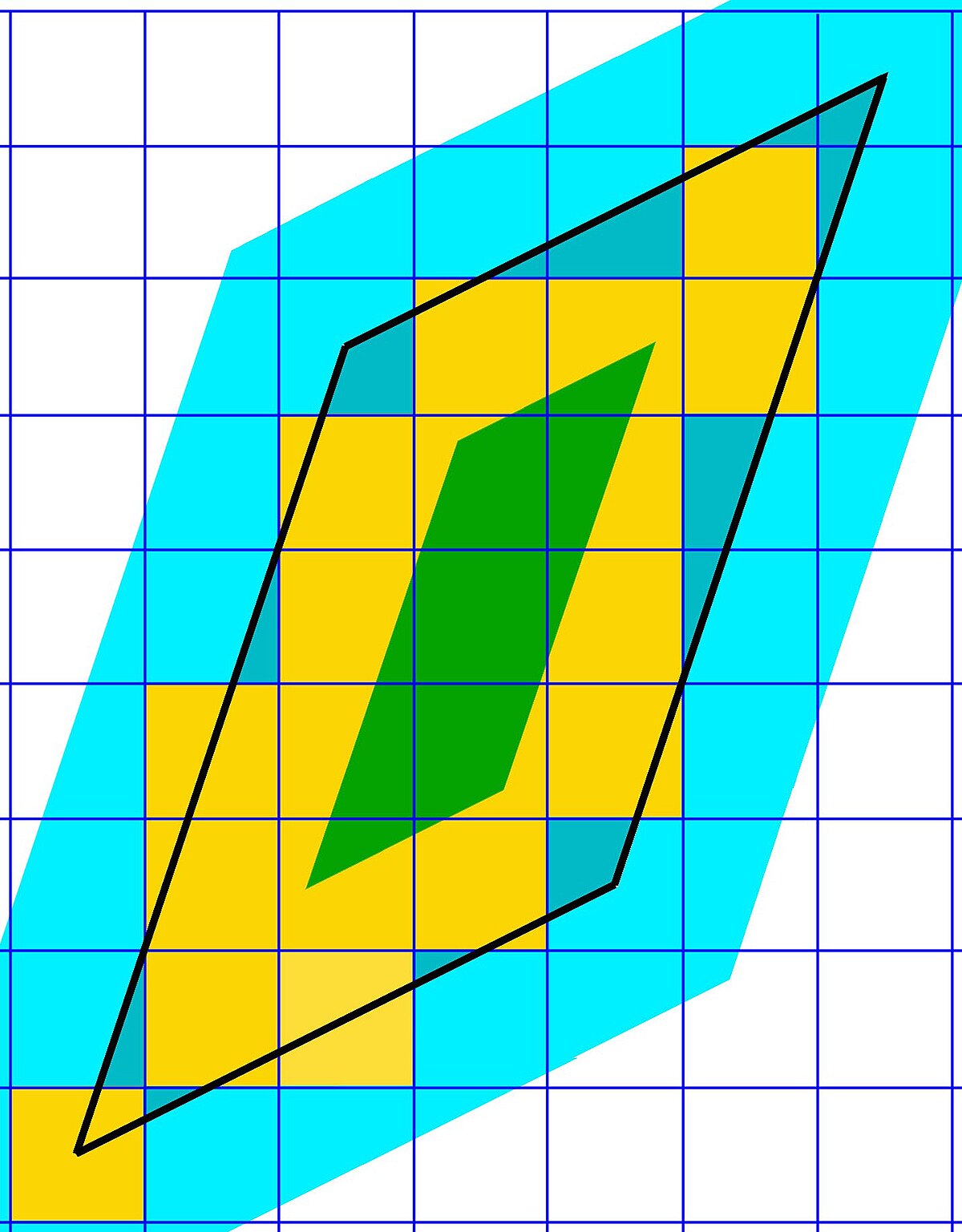
Cette propriété se démontre à l'aide de considérations issues de la géométrie arithmétique. Le corps L peut être vu comme un espace vectoriel sur Q. L'anneau OL, qui admet une base B en tant que Z module peut être vu comme un réseau, c'est-à-dire comme un sous-groupe discret de L, composé des éléments de L à coefficients dans Z pour la base B. Cette représentation est illustrée sur la figure de droite pour l'exemple Z[3√2]. Une base de l'anneau est 1, 3√2 et 3√4. Les points de l'anneau correspondent aux vecteurs de Q[3√2] à coefficients entiers dans cette base. Ils sont représentés par les petites billes sur le schéma. L'idéal des multiples de α peut être vu comme l'image de l'application linéaire φα, qui à β, un élément de l'anneau, associe α.β. Dans l'exemple, on a choisi α égal à 2 et les points de l'idéal sont en rouge sur la figure. Il forme aussi un réseau de base α.B.
Le cœur du raisonnement consiste à étudier le volume cubique rouge du schéma. Il est composé des points de coordonnées comprises dans l'intervalle [0, 1[ dans la base α.B. Comme α.B est une base de l'idéal engendré par α (l'idéal est considéré comme un Z module) cette zone porte le nom de domaine fondamental. Si l'espace est muni d'un produit scalaire euclidien conférant à B le statut de base orthonormale, le volume du domaine fondamental, encore appelé volume fondamental, est égal à la valeur absolue du déterminant de φα, ou encore à la valeur absolue de la norme de α. Sur la figure, cette norme est égale à 8 car φα est une homothétie de rapport 2 dans un espace de dimension 3. Sur la figure, on remarque bien que le cube rouge est formé de 8 petits cubes de côté 1, (par définition du produit scalaire choisi, les vecteurs 1, 3√2 et 3√4 sont de longueur 1).
Ce domaine fondamental contient exactement autant de points de l'anneau que le cardinal du quotient OL/ αOL. Dans l'exemple, il est simple de s'en rendre compte. Si β est un point quelconque de OL, il est congru au point dont les coordonnées sont le reste des divisions euclidiennes de celles de β par 2, modulo αOL. Il existe donc un unique représentant d'une classe de OL/ αOL dans le domaine fondamental. Dans l'exemple, on remarque qu'il existe exactement 8 classes, dont les représentants dans le domaine fondamental sont les points de coordonnées 0 ou 1 dans la base B. Ils sont représentés en bleu sur la figure.
Le principe de la démonstration consiste à étudier le volume formé par l'union des cubes de côté 1 et de centre les points de l'anneau inclus dans le volume fondamental. Sur la figure, on obtient un volume correspondant au translaté du domaine fondamental par le vecteur -1/2(1 + 3√2 + 3√4). L'égalité de ce volume et du volume fondamental permet de conclure et justifie la définition suivante :
-
- Soit J un idéal de OL, la norme de l'idéal J est égale au cardinal de l'anneau quotient OL / J.
Le cas particulier des entiers quadratiques, plus simple, est étudié dans l'article Idéal de l'anneau des entiers d'un corps quadratique. Toujours si K est égal à Q la propriété de multiplicativité est conservé :
-
- Soit J1 et J2 deux idéaux de OL, l'égalité suivante est vérifiée :
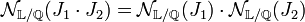
La démonstration se fonde sur le fait que l'anneau OL est de Dedekind. Tout idéal est produit d'idéaux premiers et tout idéal premier est maximal. Il suffit de démontrer que la propriété est vraie pour les idéaux maximaux et multiplier par les facteurs premiers de J2.
Enfin :
-
- Soit f un morphisme bijectif de Z module de OL vers un idéal J, la norme relative de J est égale à la valeur absolue du déterminant de f.
-
- La valeur absolue de la norme relative d'un entier algébrique α de L sur Q est égal à l'ordre de l'anneau quotient OL/ α.OL :
Soit B = (b1, ..., bd) une base de OL et donc de L. La famille α.B égale à (α.b1, ..., α.bd) est aussi une base de L en tant que Q espace vectoriel et une base de α.OL comme Z module. Tout élément γ de OL s'exprime comme combinaison linéaire de la famille α.B à coefficients dans Q, γ est élément de α.OL si et seulement si les coefficients sont des entiers relatifs. Soit F l'ensemble des points de L dont les coordonnées dans la base α.B sont éléments de l'intervalle [0,1[.
Cette configuration est illustrée sur la figure de droite, correspondant à l'anneau des entiers de Gauss et à α = 2 + i. Les points de l'anneau correspondent aux intersections du quadrillage, les point de l'idéal sont en verts et F est la surface illustrée en rouge.
-
- Montrons que chaque classe de OL/ α.OL contient un unique représentant dans F :
Soit γ un représentant d'une classe de OL/ α.OL. Soit (ci) ses coordonnées dans la base de L α.B. Sur la figure, la classe est représenté par les points bleus, le point γ peut, par exemple être choisi égal à 3 + 2.i.
Décomposons ci en la somme de sa partie entière pi et d'un reste ri éléments de [0, 1[. Les éléments de OL π et ρ sont définis par :
![\gamma = \sum_{i=1}^d c_i\alpha.b_i = \pi + \rho \quad \text{avec}\quad \pi = \sum_{i=1}^d p_i\alpha b_i,\; \rho = \sum_{i=1}^d r_i\alpha b_i\quad \text{car}\quad \forall i \in [1,d]\quad a_i = p_i + r_i](https://static.techno-science.net/illustration/Definitions/autres/f/f76fbfc22737d62ed7d971f0b2bee877_0983e26af5a2d8ea3e3e7bf1450cc1c9.png)
La famille (pi) est composée d'entiers relatifs et α est élément de α.OL, la famille (ri) est composée d'éléments de l'intervalle [0,1[ et ρ est élément de F et de OL car ρ = γ - π. La classe de γ possède un représentant ρ dans F. L'unicité résulte du fait que la différence des coordonnées de deux éléments de F dans la base α.B ne peut être entière. Sur la figure, le point ρ est égal à 1 + i, il correspond bien à l'un des 5 points de l'intersection de l'anneau et de F, en rouge sur la figure.
-
- Montrons que F contient exactement NK/Q(α) éléments dans OL :
Le raisonnement utilisé est géométrique, il est de même nature que celui du théorème de Minkowski sur le nombre de points entiers dans un convexe symétrique par rapport à l'origine.
Soit m un entier naturel strictement positif et V le volume de K constitué par les vecteurs de coordonnées en valeur absolue inférieures à m dans la base α.B. On remarque de les translations de F par des vecteurs de coordonnées entières strictement inférieurs à m - 1, en valeur absolue, dans la base α.B forment une partition de V. La démonstration précédente montre de plus que chaque translaté contient exactement autant de points de OL que F. Si Vp et Fp désignent le nombre de points de OL dans V et F, l'égalité suivante est vérifiée :
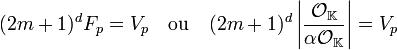
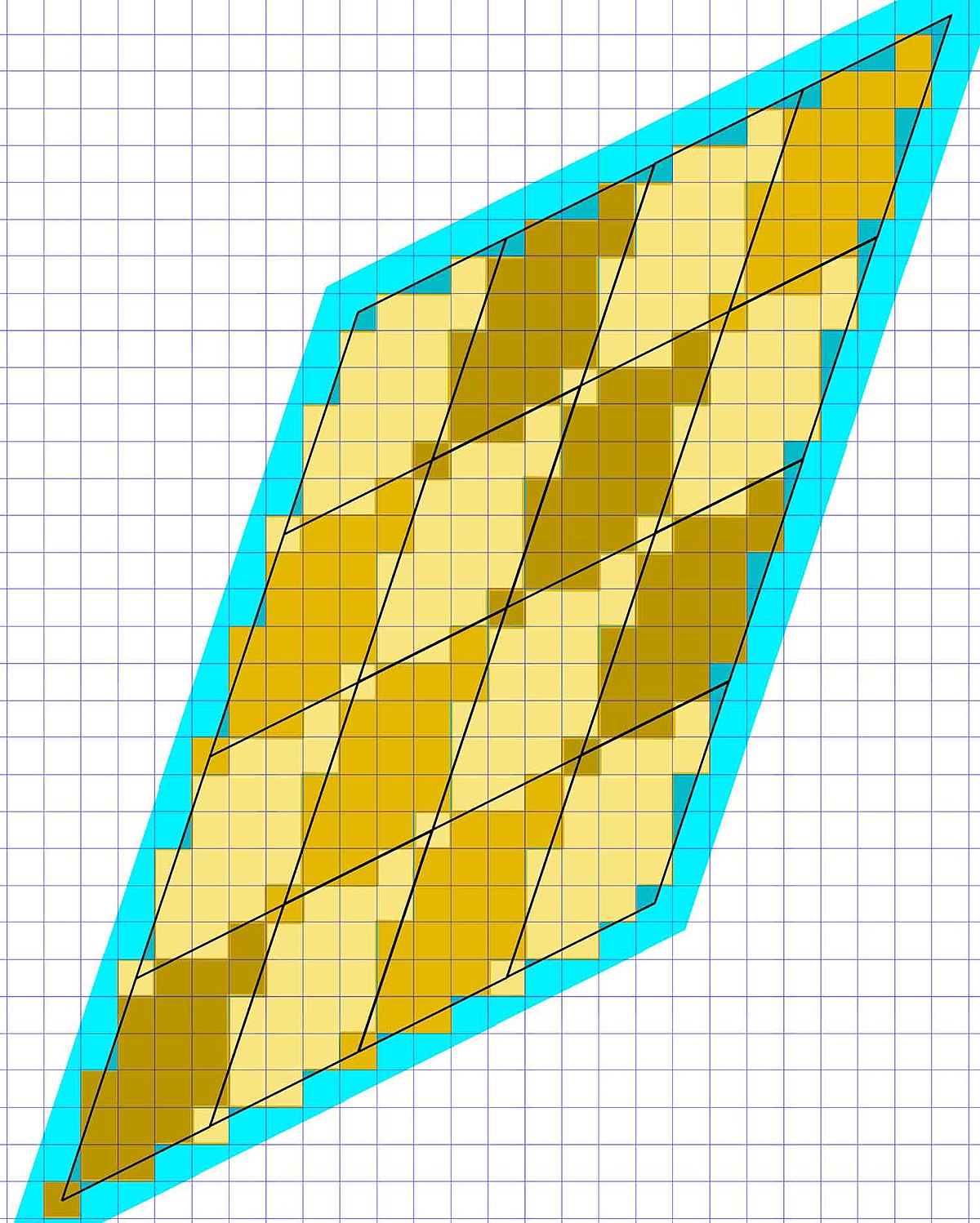
La deuxième forme est la conséquence du résultat démontrée précédemment, le signe de la valeur absolue est utilisé ici pour désigner le cardinal de l'ensemble. Cette situation est illustrée en dimension 2 par les figures à droite et à gauche. La figure de gauche représente F, les points de l'intersection de F et de l'idéal sont au centre d'un carré jaune, le volume F est à l'intérieur de la frontière, en noir. La figure de droite représente V, ce volume est constitué de 16 volumes égaux à F ou à un translaté de F. L'égalité précédente exprime le fait qu'il existe exactement autant de petits carrés jaunes dans chaque volume translaté, autrement dit, ces petits carrés s'emboitent parfaitement.
Il existe une autre manière d'évaluer Vp, il consiste à établir le volume Vv de V. On munis l'espace d'un produit scalaire conférant à B le statut de base orthonormale. Considérons un pavage de l'espace par des cubes de côtés de longueur 1, dont les arêtes sont parallèles à un vecteur de la base B et dont le centre est un point de OL. Ils correspondent aux carrés jaunes des deux figures. Soit Vv-1 le volume constitué par l'ensemble des cubes strictement inclus dans V et Vv+1 celui constitué par l'ensemble des cubes ayant une intersection non vide avec V. On obtient les majorations suivante :
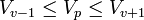
Si S est la surface frontière du volume V et Sv sa mesure, on obtient :
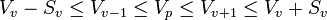
Soit M un majorant de la mesure de la plus grande face du volume fondamental F, comme il existe 2.d faces et que chaque face du volume V est composée de (2m+ 1)d-1 faces de F, on obtient les majorations suivantes :
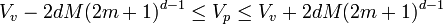
Enfin Vv est l'image d'un volume de mesure égale à (2μ + 1)d par une application linéaire de déterminant NL/Q(α). En utilisant la valeur de Vp calculée précédemment, on obtient :
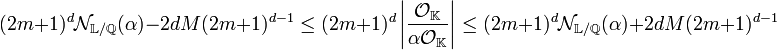
En simplifiant par (2m + 1)d les majorations :
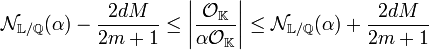
Si m est choisi plus grand que d.M, le fait que la norme relative de α et le cardinal du quotient soit des entiers naturels permet de conclure.
-
- Soit f un morphisme bijectif de Z module de OL vers un idéal J, la norme relative de J est égale à la valeur absolue du déterminant de f.
Remarquons tout d'abord qu'un tel morphisme existe toujours. Le module OL est noethérien car l'anneau associé est de Dedekind. Un idéal est un sous-module de même dimension que le corps, il admet une base. Toute application ayant bijective de B une base de J se prolonge en un morphisme de Z module bijectif.
Le raisonnement précédent s'applique encore. Il suffit de considérer comme volume fondamental l'ensemble des vecteurs de coordonnées élément de [0, 1[ dans la base image de B par f.
-
- Soient J1 et J2 deux idéaux de OL, l'égalité suivante est vérifiée :
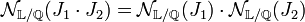
L'idéal J2 est un produit d'idéaux premiers (cf idéal fractionnaire). Il suffit donc de démontrer la proposition si J2 est premier, le cas général se traitant alors par multiplication successives d'idéaux premiers.
Considérons la structure OL / J1.J2. Elle peut être considérée comme le quotient d'un groupe additif par un sous-groupe. Il existe un morphisme de groupe canonique φ entre cette structure et OL / J1. En effet, si deux éléments de OL diffèrent par un élément de J1.J2, ils diffèrent d'un élément de J1 et ont même image dans OL / J1 et ce morphisme est surjectif. La théorie des groupes montre que si |Ker φ| désigne l'ordre du groupe noyau de φ :
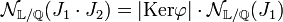
Le noyau de φ est composé des éléments des classes des éléments de J1 dans OL / J1.J2, c'est-à-dire J1 / J1.J2. On va montrer que ce noyau peut être vu comme un espace vectoriel de dimension 1 sur le corps OL / J2. Comme J2 est un idéal premier donc maximal, ce quotient est bien un corps. Remarquons qu'il opère bien sur J1 / J1.J2, soient deux éléments de OL dont la différence est un élément de J2, les produits de ces deux éléments par un membre de J1 diffèrent par un élément de J1.J2, ce qui signifie que leur classe est bien la même dans J1 / J1.J2. La structure J1 / J1.J2 est bien celle d'un groupe abélien sur lequel opère un corps. Cette structure est celle d'un espace vectoriel.
Il reste encore à montrer que cet espace est de dimension 1. Soit α un élément de J1 qui n'est pas dans J1.J2. Un tel élément existe car sinon J1 serait égal à J1.J2 et cet idéal disposerait de deux décompositions en idéaux premiers, ce qui est impossible. L'objectif est de montrer que la classe de α est un vecteur générateur de l'espace vectoriel J1 / J1.J2. Soit A l'idéal engendré par α. C'est un idéal contenu dans J1, ce qui montre que J1-1.A est un idéal de OL, noté ici B. L'idéal A est égal à J1.B. La somme des idéaux A et J1.J2 est égal à J1. En effet cette somme est égal à J1(B + J2). L'idéal B n'est pas strictement inclus dans J2 car α n'est pas un élément de J1.J2, ce qui montre que B + J2 est un idéal contenant strictement l'idéal principal J2, c'est-à-dire est égal à OL, ce qui montre que la somme de A et de J1.J2 est égal à J1. Soit β un élément quelconque de J1, on va montrer que la classe de β est générée par celle de α. La remarque précédente montre l'existence d'un élément k de OL tel que k.α diffère de β par un élément de J1.J2. En d'autre termes, la classe de k dans le corps OL / J2 multipliée par la classe de α, dans l'espace vectoriel J1 / J1.J2 est égale à la classe de β dans ce même espace vectoriel.
On a montré que J1 / J1.J2, en tant qu'espace vectoriel, est de dimension 1, car engendré par la classe de β. Le cardinal de l'espace vectoriel est égal à celui de son corps ou encore à celui de la norme de J2. Autrement dit, le noyau de φ est de cardinal la norme de J2, ce qui termine la démonstration.