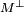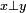Orthogonalité - Définition

Généralisation du concept

Arithmétique

Un nombre premier est somme de deux carrés s'il se trouve sur un cercle dont le carré du rayon est entier. Cette remarque introduit l'orthogonalité dans l'arithmétique.

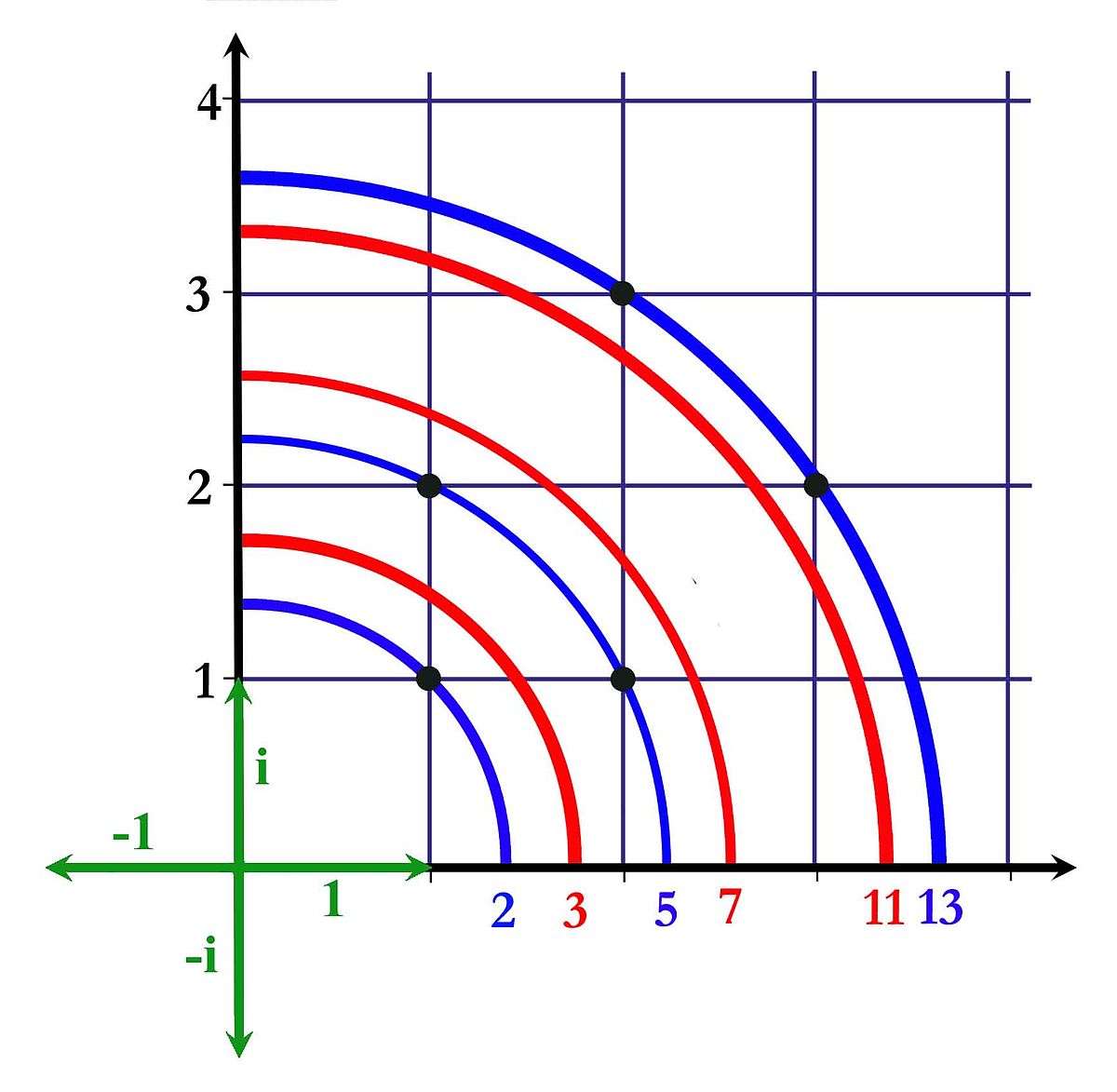
D'autres questions, bien éloignées de la géométrie du triangle sont finalement résolues avec l'orthogonalité. En 1640 Pierre de Fermat se pose la question de savoir quels nombres premiers sont somme de deux carrés. La question est d'apparence anodine, cinq et treize vérifient cette propriété, sept et onze non. Fermat devine juste en conjecturant que tout nombre premier impair dont le reste de la division par quatre est égal à un est somme de carré, mais comment le démontrer ? Plus d'un siècle et le talent d'Euler sont nécessaire pour en venir à bout. L'équation x² + y² = p est enfin résolue, elle fait partie d'une interrogation plus vaste, dans quel cas l'équation x² + n.y² = p admet-elle une solution entière? De manière plus générale, dans quel cas l'équation suivante à coefficients entiers admet-elle une solution entière :

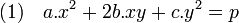
Une telle expression est appelée une forme quadratique. Lagrange propose une démarche originale, il remarque que, sous réserve de bonnes propriétés sur les coefficients a, b et c, la formule (1) représente le carré de la distance du point (x, y) à l'origine. La question est alors de savoir dans quel cas il existe deux vecteurs à coefficients entiers orthogonaux et de longueur un. Lagrange trouve la condition nécessaire et suffisante qui lui permet de conclure. Ce raisonnement lui permet de résoudre l'équation x² + n.y² = p si n est égal à un, deux, trois, quatre ou cinq. Le cas général reste hors de portée. Il faut encore plus d'un siècle d'efforts et le talent de nombreux géomètres, souvent allemands pour en venir à bout. L'arithmétique fait usage de l'orthogonalité, cependant, à la différence des grecs, les nombres associés ne sont plus les réels mais les entiers. La théorie voit un enrichissement à d'autres ensembles de nombres.

Dimension quelconque

Comme toutes les quadriques, un ellipsoïde possède des axes principaux orthogonaux. Cette propriété permet leur classification.

Une autre question impose une nouvelle généralisation. Depuis Newton, la trajectoire des planètes, essentiellement sous l'influence du soleil est relativement bien connue. Cependant, les planètes s'attirent entre elles, créant de petites perturbations par rapport à l'approximation de Newton, appelées variations séculaires. Lagrange cherche à démontrer que les variations du premier ordre ne peuvent déstabiliser le système. Augustin Louis Cauchy découvre que cette question est aussi associée à une forme quadratique. Il remarque qu'une équation de type (1) généralisée à la dimension trois définit une surface quadrique comme l'ellipsoïde de la figure de droite. Trouver les bons vecteurs orthogonaux pour cette quadrique lui permet de les classifier toutes. Cette méthode résout aussi la question de Lagrange dans le cas où seul trois planètes sont prises en compte.

La preuve de Cauchy est parcellaire, il existe plus de trois planètes. Pour résoudre le cas général, il faut pouvoir trouver autant de vecteurs orthogonaux qu'il existe de planètes. Cette question, consistant à trouver une bonne famille de vecteurs orthogonaux pour une forme quadratique est finalement résolue par Karl Weierstrass en 1858. Si l'avancée mathématique est certaine, la preuve de la stabilité du système solaire n'est toujours pas faite. l'astronome Urbain Le Verrier montre que les termes d'ordre deux ne peuvent être négligés.

Si les conséquences en astronomie restent douteuses, une chose est néanmoins établie. L'orthogonalité ne peut plus se limiter à la dimension trois, les services qu'elle rend sont appréciables en mathématiques comme en physique sur des espaces de dimension quelconque.

Forme bilinéaire

La généralisation n'est néanmoins pas encore totale. Vers la fin du XIX^e siècle Ferdinand Georg Frobenius découvre une nouvelle méthode pour étudier les groupes finis. Il les représente par un groupe d'applications linéaires. Il démontre que, pour un groupe donné, chaque représentation est construite à partir d'un nombre fini de briques élémentaires. Pour chacune de ces briques élémentaires, il considère une fonction, qui à chaque élément du groupe associe la trace de l'application linéaire associée. Cette application s'appelle le caractère de la représentation. Les caractères des briques élémentaires sont tous orthogonaux entre eux. Cette propriété permet de déterminer simplement quelles briques élémentaires sont utilisées pour une représentation donnée. Elle est un des fondements de la théorie. Cette orthogonalité s'exprime à l'aide d'une forme bilinéaire symétrique, absolument équivalente à une forme quadratique.

Les groupes apparaissent comme un sous-ensemble de rotations dans l'espace. Si les ensembles de nombres choisis sont finis, le groupe des rotations est nécessairement fini. Cette méthode permet de construire des groupes simples, briques élémentaires pour la construction de tout groupe fini. Ces ensembles de nombres ne sont plus ordonnés, l'équivalent de la distance ne peut donc être toujours positive. Frobenius n'est de loin pas le premier à s'intéresser à cette configuration. Euler étudiait déjà en arithmétique un problème analogue à celui de Fermat : x² - n.y² = 1 avec une forme quadratique pas toujours positive. James Joseph Sylvester trouve en 1852 une loi portant son nom qui indique que toutes les bases orthogonales contiennent le même nombre de vecteurs ayant une distance positive et le même nombre ayant une distance négative. Le concept d'orthogonalité s'applique alors à une forme bilinéaire, qui ne correspond plus nécessairement à une distance euclidienne. En effet, au sens propre, une distance est toujours positive.

Le formalisme moderne est plus tardif que la découverte des théorèmes fondamentaux. Les mathématiciens les découvrent souvent bien avant qu'une présentation simple et didactique soit disponible. Par exemple, le produit scalaire est une forme bilinéaire correspondant à une géométrie euclidienne. Sa définition est l'œuvre d'Hermann Weyl et date de 1918. Avec ce formalisme, les termes angle droit et perpendiculaire ne sont plus utilisés.

Définitions formelles

Soit (.|.) une forme bilinéaire définie sur ExF deux espaces vectoriels sur un corps K.

Définition 1 —  Soit M (resp. N) une partie de E (resp. F). L'orthogonal de M (resp. N) correspond à l'ensemble des vecteurs y (resp. x) de F (resp. E) vérifiant la propriété suivante :

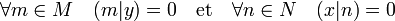
L'orthogonal de M (resp. N) désigne ainsi l'ensemble des vecteurs de E (resp. F) perpendiculaires à tous les éléments de M (resp. N). Néanmoins, dans le contexte général de cette définition les termes de perpendiculaires et angle droit ne sont plus utilisés.

Définition 2 —  Deux vecteurs x et y de E et F sont dit orthogonaux pour la forme bilinéaire si et seulement si leur image par la forme bilinéaire est nulle :

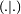
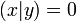
D'une manière plus générale, on dit qu'un ensemble M est orthogonal à un ensemble N si, pour tout élément m de M et tout élément n de M, l'image (m | n) est nulle.

L'orthogonal d'un ensemble M est souvent noté et la proposition x est orthogonal à y s'écrit .