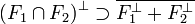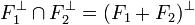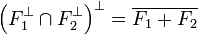Orthogonalité - Définition
La liste des auteurs de cet article est disponible ici.
Informatique
Le jeu d'instructions d'un ordinateur est dit orthogonal lorsque (presque) toutes les instructions peuvent s'appliquer à tous les types de données. Un jeu d'instruction orthogonal simplifie la tâche du compilateur puisqu'il y a moins de cas particuliers à traiter : les opérations peuvent être appliquées telles quelles à n'importe quel type de donnée. Un exemple typique est le VAX ou le PDP-10.
Dimension infinie
Motivation

En dimension finie, l'orthogonalité rend d'innombrables services. Il est tentant de généraliser sa définition aux espaces de dimensions quelconques et en particulier infini. Sous un formalisme un peu différent, c'est ainsi que Joseph Fourier résout l'équation de la chaleur. A deux fonctions f et g, on associe le produit scalaire :
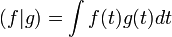
Certain problèmes issues de la physique, comme l'équation de la chaleur ou celle de la corde vibrante s'exprime comme un opérateur linéaire disposant de bonnes propriétés vis-à-vis de son adjoint. Si la configuration est particulièrement favorable, par exemple si l'opérateur est compact et autoadjoint, un résultat analogue à celui de la dimension finie apparaît. Il existe une base de vecteurs propres orthogonaux et de norme un. Le mot base prend ici une signification un peu différente de celle de la dimension finie. La famille est toujours libre, cependant ce n'est plus une combinaison linéaire qui représente un vecteur mais une série dont le carré de la norme de chaque vecteur est absolument convergente.
Puisqu'en dimension infinie les combinaisons linéaires deviennent des séries, un nouvel outil devient indispensable, la topologie, permettant de donner un sens à la limite, c'est-à-dire à l'équivalent des combinaisons linéaires. Dans le cas général, cette limite n'est garantie d'exister que si l'espace est complet. Pour cette raison, le cadre le plus simple pour étudier l'orthogonalité en dimension finie est celui d'un espace vectoriel muni d'un produit scalaire tel que la distance associée confère à l'espace la complétude. Plusieurs mathématiciens sont initiateurs de l'étude de la géométrie d'un espace vectoriel de cette nature, on peut citer Erhard Schmidt ou encore Ivar Fredholm . David Hilbert est néanmoins celui qui lui donne son nom. John von Neumann donne la définition moderne du concept.
Il existe certaines configurations où l'espace fonctionnel ne peut être équipé d'un produit scalaire. Une autre technique permet de bénéficier des propriétés d'orthogonalités, provenant de l'espace dual. En général n'est considéré que le dual topologique, c'est-à-dire celui ne contenant que les formes linéaires bornées. Une fois encore l'hypothèse de la complétude de l'espace vectoriel E est fort utile. Stefan Banach propose la première formulation axiomatique moderne. Son livre de 1932 sur la question est encore une référence. Un espace de Banach est un espace vectoriel normé complet.
Espace de Hilbert
Espace de Banach
Dans ce paragraphe E désigne un espace de Banach et E* son dual topologique, l'unique dont il est question ici. Ainsi le produit scalaire est remplacé par une forme bilinéaire souvent noté avec le crochet de dualité <.,.> utilisé dans ce paragraphe. Cette forme, encore parfois appelée produit scalaire, est l'unique étudiée ici. En effet, toute forme bilinéaire d'un espace E dans un espace F est la composée d'un opérateur linéaire a de F dans le dual de E et du crochet de dualité. Les propriétés d'une telle forme bilinéaire sont les conséquences de celle de a et de son adjoint.
La définition de l'orthogonalité est l'application de la définition générale. Ainsi, l'orthogonal d'une partie Ψ* du dual est le sous-espace vectoriel de E composé des vecteurs orthogonaux à tous les vecteurs de Ψ*. On remarque qu'une autre définition aurait pu être utilisée, l'ensemble des éléments du bidual orthogonaux à Ψ*. Il existe une isométrie canonique entre E et le bidual, qui à x associe x** définie par :
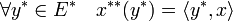
Dire que E est un espace réflexif revient à dire que l'isométrie est surjective et qu'il est possible d'identifier E avec le bidual. Dans toute la suite du paragraphe, l'orthogonal d'une partie de E* désigne toujours un sous-espace vectoriel de E, même si l'espace n'est pas réflexif.
Proposition 1 — Soit F un sous espace vectoriel de E, l'orthogonal de
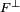
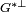
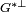
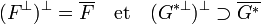
La proposition 2 pour les espaces euclidiens prend une forme légèrement différente :
proposition 2 — Soit F1 et F2 deux sous-espaces vectoriels fermés de E alors :
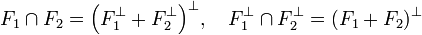
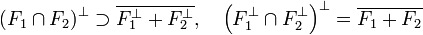
Si F1 + F2 est un sous-espace fermé, alors la situation est proche de la configuration euclidienne. Le résultat suivant est plus profond, en conséquence, il est plus subtile à démontrer :
proposition 3 — Les quatre propositions suivantes sont équivalentes :
-
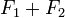
-
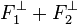
-
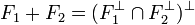
-
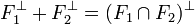
-
- L'orthogonal de
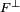
- L'orthogonal de
Remarquons dans un premier temps qu'un orthogonal est un sous espace fermé. Soit (xn) une suite de l'orthogonal d'une famille Φ* convergeant vers x. Soit x* un élément de Φ* :
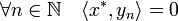
Un passage à la limite montre que y est aussi élément de l'orthogonal de Φ*. L'adhérence de F est donc contenu dans l'orthogonal de
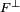
Réciproquement raisonnons par l'absurde. Soit x un élément de l'orthogonal de
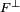
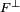
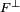
-
- L'orthogonal de
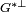
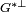
- L'orthogonal de
Montrons que
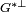
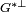
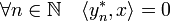
Un passage à la limite montre que y est orthogonal à x et donc orthogonal à
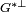
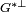
Réciproquement, supposons E réflexif. On raisonne par l'absurde comme précédemment. Soit y* un élément de l'orthogonal de
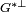
-
- Proposition 2 :
-
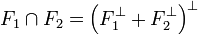
Soit x un élément de l'intersection, il est orthogonal à tout élément de
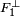
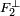
Réciproquement, la somme des orthogonaux de F1 et F2 contient tout élément de l'orthogonal de l'intersection de F1 et F2. Comme l'intersection de deux fermés est un fermé, la proposition 1 permet de conclure que :
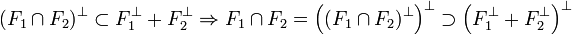
Ce qui termine la démonstration.
C'est une conséquence de la proposition précédente et de la proposition 1.
Considérons un élément de l'intersection, il est par définition orthogonal à tout élément de F1 et de F2. L'intersection est donc incluse dans l'orthogonal de la somme. Réciproquement soit un élément de l'orthogonal de la somme. Il est, par définition orthogonal aux élément de F1 et de F2, ce qui termine la démonstration.
C'est une conséquence de la proposition précédente et de la proposition 1.
-
- Les quatre propositions suivantes sont équivalentes :
-
-
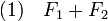
-
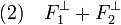
-
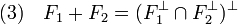
-
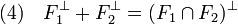
-
- (1) est équivalent à (3) :
Cette proposition est une conséquence directe de la proposition précédente.
- (4) implique (2) :
Si (4) est vraie, alors la somme est égal à un orthogonal, comme tout orthogonal est fermé, la somme est fermée.
- (1) implique (4)
Réciproquement, si (2) est vraie, une proposition précédente montre que la somme des orthogonaux est incluse dans l'orthogonal de l'intersection. Soit y* un élément de l'orthogonal de l'intersection. Soit G la somme de F1 et de F2. Tout élément x de G est somme d'un élément x1 de F1 et d'un élément x2 de F2. Soit z2* l'application qui à x associe < y* , x1>. Comme y* est la forme linéaire nulle sur l'intersection de F1 et F2, l'image de x par z2* est bien définie. La forme z2* est clairement liénaire. De plus, un corollaire du théorème de Banach-Schauder, dit de l'application ouverte montre qu'il existe une constante C strictement positive telle que (la démonstration du corollaire est donnée dans l'article associée):
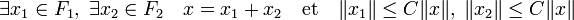
Cette propriété montre la continuité de z2*. Le théorème de Hahn-Banach sous sa forme géométrique montre qu'il est possible de prolonger z2* en une forme linéaire continue y2* sur E. Définissons y1* comme la différence y* - y2*. La forme y1* est nulle sur F1 et y2* est nulle sur F2. Ce qui montre que y* est bien élément de la somme des orthogonaux.
-
- (2) implique (1) :
Applications
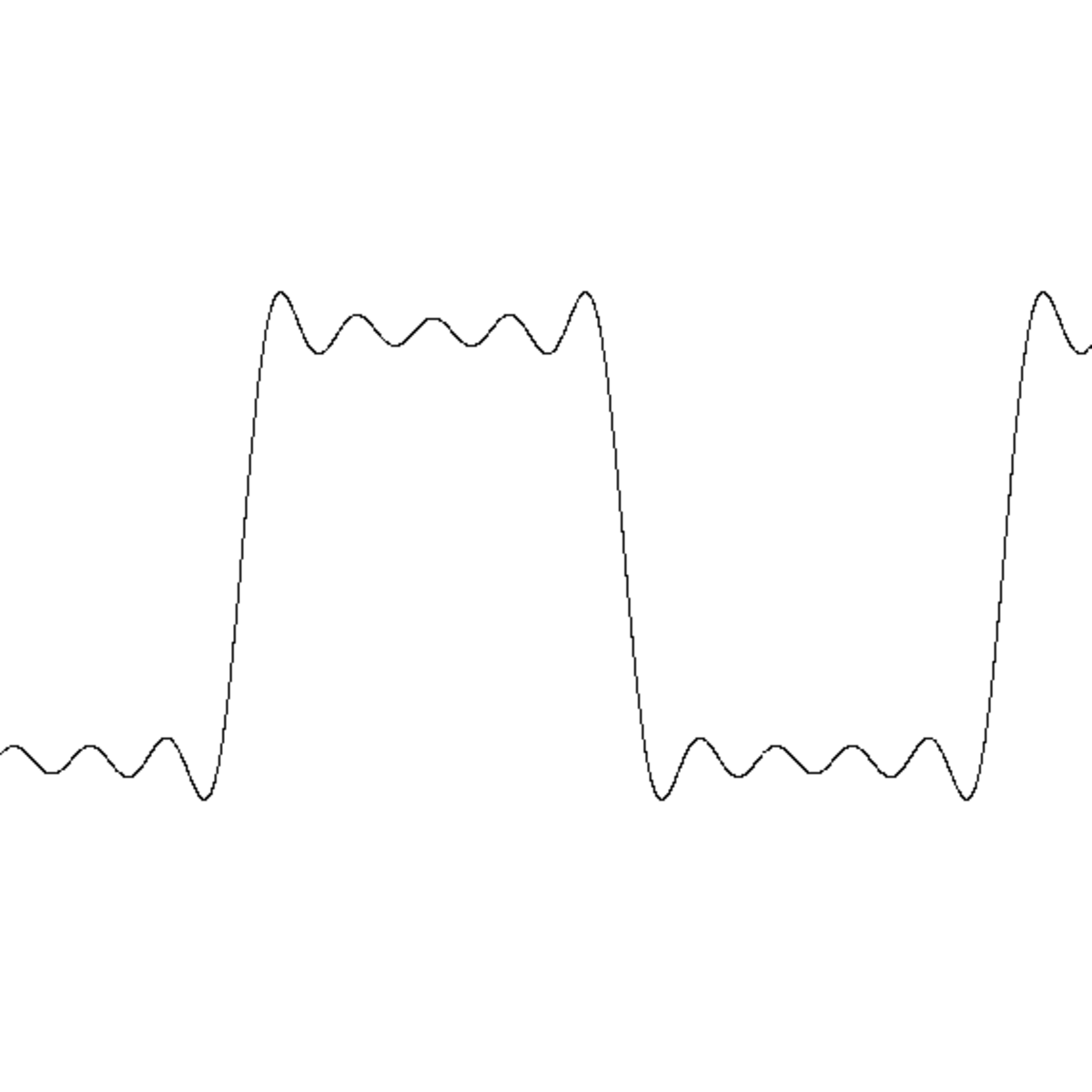
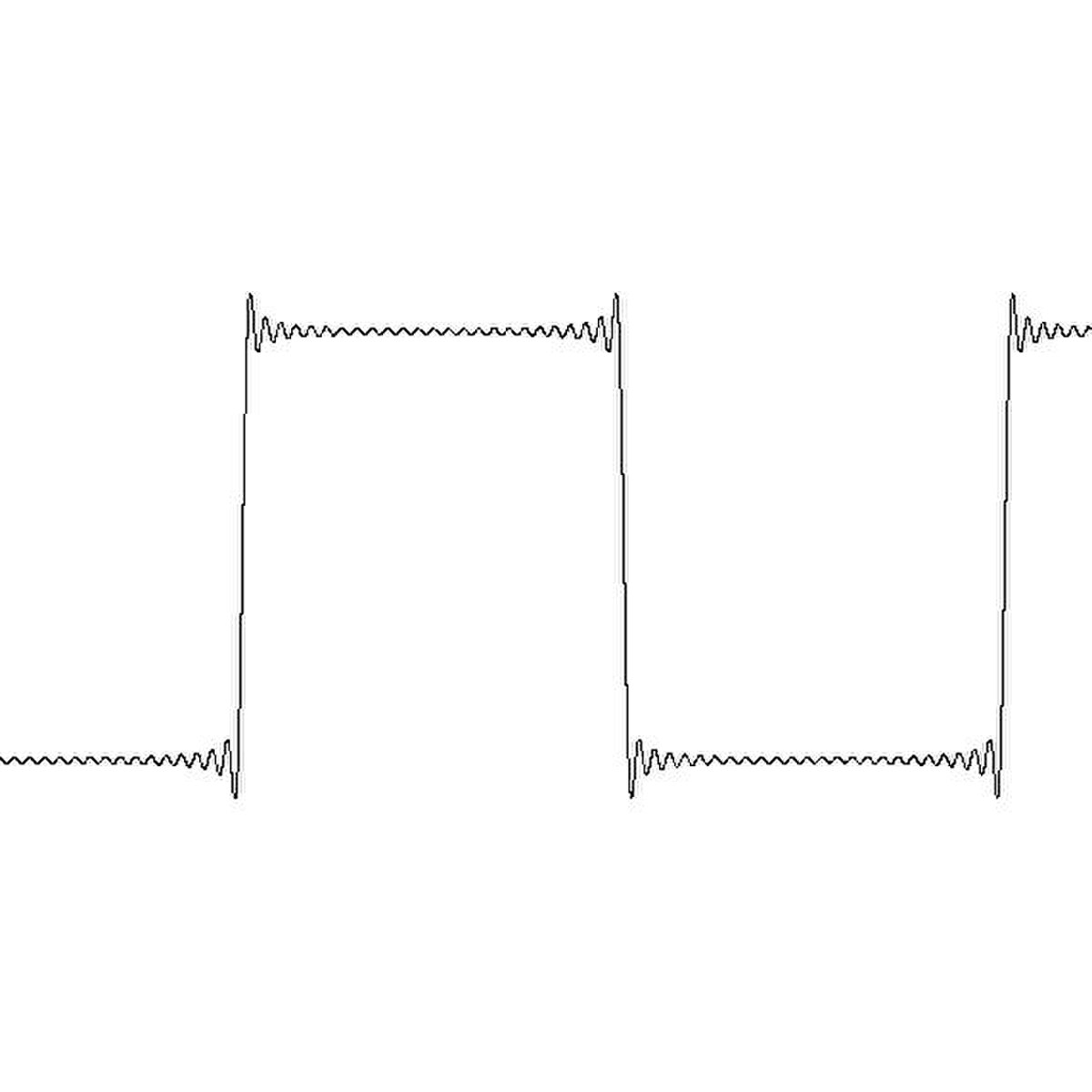
La première application historique de l'orthogonalité en dimension infinie a pour objectif de résoudre une équation aux dérivées partielles. La nature offre de nombreux exemples où l'équation se traduit par un opérateur linéaire. Tel est le cas, par exemple pour l'équation d'onde qui régit les mouvements d'une corde vibrante. Cette équation se résout simplement si la position initiale de la corde est une sinusoïde de période la longueur de la corde divisée par un entier. Ces cas particuliers possèdent deux propriétés importantes. L'espace vectoriel approxime aussi précisément que souhaité toutes les positions initiales que peut prendre la corde (elle est supposée ne pas rompre, ce qui signifie que la position initiale est représentée par une fonction continue). De plus cette famille sinsoïdale est orthogonale, l'inégalité de Bessel permet de déterminer une combinaison linéaire qui approxime aussi précisément que souhaité la position initiale ou propose une série convergente vers cette position. Les figures de droite et de gauche illustrent deux approximations de la fonction créneau. La linéarité de l'opérateur permet d'évaluer la trajectoire de la corde par combinaison linéaire ou série. Cette technique, consistant à décomposer une fonction sur une famille orthogonale est à l'origine d'une vaste branche des mathématiques, appelée analyse harmonique.
Pour cette raison, de nombreuses familles orthogonales ont été construites. Les polynômes orthogonaux, comme ceux de Legendre, d'Hermite ou de Laguerre sont de cette nature. Ils correspondent à trois produits scalaires différents.
Le théorème de Weierstrass possède son équivalent sur un Hilbert. L'opérateur doit non seulement être autoadjoint mais aussi compact. Cette configuration correspond à une équations intégrales étudiée par Hilbert et Schmidt. Comme en dimension finie, il existe une base de vecteurs propres orthogonaux. Cette équation intégrale possède une signification profonde en physique, elle représente par exemple les équations de Maxwell.
La bonne propriété topologique de compacité n'est pas toujours présente. L'équation de Schrödinger est un exemple d'opérateur autoadjoint non compact, il n'est d'ailleurs pas continu. S'il existe toujours des vecteurs propres et s'ils sont toujours orthogonaux, ils ne forment plus une base de l'espace des solutions. Une fois encore, il est nécessaire d'élargir les définitions pour que les concepts restent opérationnels. Une valeur λ est dite spectrale pour l'opérateur a si a -λ.Id n'est pas inversible. Il se peut que a -λ.Id soit injectif et non surjectif. Dans ce cas, il n'existe pas de vecteur propre. Une autre théorie devient nécessaire, appelée théorie spectrale.
La physique ne se contente pas des espaces de Hilbert. Un phénomène peut être suffisamment discontinu pour sortir du Hilbert, il est parfois modélisé par un pic de Dirac, une espèce de fonction valant zéro partout sauf en un point ou elle vaudrait l'infini. Elle représente par exemple une probabilité de présence nulle partout sauf en un point où la position est certaine. Pour enrichir l'espace fonctionnel, il devient nécessaire d'utiliser des Banach et la théorie des distributions. Le produit scalaire devient le crochet de dualité.
Si la physique est à l'origine de la généralisation de l'orthogonalité aux dimensions infinies, elle n'est de loin pas la seule cliente. La théorie des représentations s'étend aux groupes continus. Les caractères deviennent des fonctions du groupe à valeur dans les nombres complexes. A l'aide d'une mesure, comparable à l'intégrale sur les réels, un produit scalaire est défini. Les relations d'orthogonalités du cas fini se généralisent. Une fois encore, la décomposition en briques élémentaires est donnée par des relations d'orthogonalités entre les caractères. Cette approche consistant à décomposer une fonction sur une famille orthogonale est de même nature que celle utilisée pour étudier les mouvements d'une corde vibrante. Si le groupe choisi est celui des nombres complexes de module un, les résultats obtenus sont identiques. on retrouve par un autre chemin la théorie de l'analyse harmonique. Il devient possible de la généraliser à bien d'autres groupes.