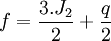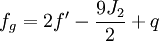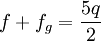Sphéroïde de Clairaut - Définition

Théorème de Clairaut

Parmi les résultats essentiels obtenus par Clairaut, citons les suivants : Soit un corps de révolution symétrique par rapport à l'équateur, de rayon équatorial a et de rayon polaire c, et supposons que l'aplatissement géométrique défini par le rapport , est petit. Dénotons par u l'angle que fait la verticale en un point quelconque M de la surface avec l'axe des pôles. L'équation de cette surface, appelée sphéroïde de Clairaut, est r = a(1 − f.cos²u) en première approximation.

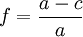
Soient γ_e et γ_p les pesanteurs à l'équateur et aux pôles, et l' aplatissement gravimétrique. Clairaut a montré que, dans ces circonstances, la pesanteur sur le sphéroïde sera de la forme γ(M) = γ_e(1 + f_g.cos²u).

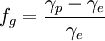
Comme l'angle u est la colatitude du point M, on se rend compte que Clairaut retrouve ainsi par la théorie le résultat que Maupertuis avait déduit d'une douzaine d'expériences pendulaires à différentes latitudes. Cette dernière équation, munie d'un terme supplémentaire très petit pour tenir compte des effets du second ordre, constitue à l'heure actuelle la formule internationale de la pesanteur. Tous les gravimétristes l'utilisent pour réduire leurs observations.

D'autre part, si ω désigne la vitesse angulaire de rotation du corps de masse M et de moments d'inertie A et C par rapport aux axes équatorial et polaire, respectivement, on définit alors le facteur de forme dynamique par et la constante géodynamique q par le rapport de l'accélération centrifuge à l'accélération de la pesanteur à l'équateur, c'est-à-dire .

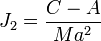
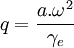
Clairaut a montré qu'entre les quatre nombres f, f_g, J₂ et q, il existe les trois relations suivantes:

La première de ces trois relations algébriques constitue le théorème de Clairaut. Elle possède une signification profonde, en ce sens qu'elle associe dans une même expression la quantité géométrique f, la quantité cinétique J₂ et la quantité dynamique q. La dernière relation est tirée des deux premières en éliminant J₂. En effet, Clairaut admet seulement que la surface du corps est de niveau constant, au sens du nivellement, celle qu'épouserait une pellicule liquide recouvrant l'entièreté de la surface. La troisième équation ci-dessus ne dépend donc pas d'éventuelles variations de la densité, ni de la structure interne du corps, pourvu que sa surface externe soit de niveau. Comme la valeur de q est bien connue et l'était déjà du temps de Clairaut, à savoir q ≅ 1/288, il suffit de déterminer le paramètre f_g, c'est-à-dire les variations de la pesanteur, pour déduire de la troisième relation l'aplatissement géométrique f. Un calcul aisé permet de vérifier que pour une densité interne constante, on trouve .

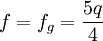
Autrement dit, on retrouve la valeur annoncée par Newton. D'autre part, pour un corps quasi-sphérique, . Dans ces conditions, la première des trois relations ci-dessus fournit f ≅ , qui est la valeur prévue par Huyghens. Qui plus est, Clairaut tira d'importantes conclusions concernant la constitution de la Terre en admettant que celle-ci, bien que solide, se comporte comme un corps en équilibre hydrostatique. C'est souvent l'hypothèse qu'on fait encore actuellement lorsqu'on étudie la structure interne de la Terre et des planètes. La théorie de Clairaut était en avance d'un siècle et demi par rapport aux possibilités techniques permettant sa pleine application. En effet, ce n'est qu'à la fin du XIX^e siècle ou au début du XX^e siècle que les méthodes géodésiques commençaient à être assez précises pour pouvoir tirer profit de cette théorie. En tout cas, elle justifiait entièrement l'interprétation des observations de Richer et elle permettait même de soupçonner des incompatibilités entre l'aplatissement que l'on pouvait déduire en utilisant la troisième relation et l'aplatissement qu'on pouvait calculer par la géométrie en attribuant au méridien un profil elliptique.

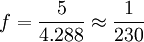
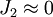
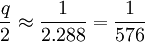
Clairaut conclut en ces termes : «… Mais la comparaison de la théorie avec les observations achèvera peut-être de décider en faveur d'un système qui a déjà tant d'apparence d'être vrai, je veux dire celui de Mr. Newton. Car l'attraction étant supposée, je démontre que, toutes les hypothèses les plus vraisemblables qu'on puisse faire sur la densité des parties internes de la terre, il y a toujours une telle liaison entre la fraction qui exprime la différence des axes et celle qui exprime la diminution de la pesanteur du pôle à l'équateur que si l'une de ces deux fractions surpasse 1/230, l'autre doit être moindre et précisément de la même quantité ; or, comme toutes les expériences que l'on a faites sur la longueur du pendule nous montrent que la diminution de la pesanteur du Pôle à l'équateur est plus grande que 1/230, on doit conclure que la différence des axes est moindre ».

En fait, les mesures pendulaires de l'époque auraient pu fournir, grâce à la troisième relation de Clairaut, des estimations de f comprises entre 1/274 et 1/303, donc assez voisines de la valeur moderne fournie par la géodésie spatiale, il n'en allait pas de même pour les mesures d'arcs de méridien. En effet, on montre que le rayon de courbure d'une ellipse méridienne dont l'aplatissement est faible est donné en bonne approximation par , où φ est la latitude et a le demi-grand axe de l'ellipse. Si nous désignons par ρ₁ et ρ₂ deux rayons de courbure se rapportant respectivement aux latitudes et (φ₂) des points moyens de deux mesures d'arc, on trouve . Or, est précisément égal au rapport des arcs de 1° mesurés par triangulation. La méridienne de Laponie avait fourni 57438 toises par degré à une latitude moyenne de 66°20', celle de France 57074 toises par degré à une latitude moyenne de 49°29' et celle du Pérou 56746 toises par degré à une latitude moyenne de 1°30' S. Notons encore la valeur amendée par Le Monnier pour l'arc Paris-Amiens de 57183 (au lieu de 57074) toises par degré à la même latitude moyenne de 49°29' que celle retenue par La Caille.

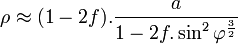
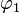
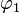
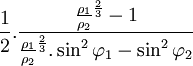
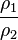
Les valeurs de f déduites de mesures d'arcs en France, en Laponie, en Equateur et au Cap de Bonne-Espérance se répartissent entre les valeurs extrêmes 1/125 et 1/1271, qui n'ont guère de signification physique. Les raisons de cette dispersion des valeurs de l'aplatissement terrestre obtenues par triangulation donnaient lieu à des discussions fort animées qui se sont poursuivies pendant très longtemps. Il s'est avéré qu'une partie de l'erreur provenait d'un désaccord d'environ 10^–3 entre la toise de Picard et celle de l'Académie. Une erreur plus importante — dont on ne s'est rendu compte que bien plus tard — s'était glissée dans les mesures astronomiques de Maupertuis en Laponie.

Comme on le voit, la période qui s'étend entre 1650 et 1750 fut marquée par des progrès inestimables, tant du point de vue expérimental et observationnel que du point de vue théorique. Elle vit la naissance et l'acceptation définitive — entre 1720 et 1740 — de la théorie de la gravitation de Newton pour expliquer le mouvement des corps célestes et la forme de la Terre et des planètes. Pendant cette époque, la géodésie et l'astronomie géodésique connurent un essor sans précédent. Celui-ci fut au départ à peu près exclusivement à mettre au compte de savants français qui, sous l'égide de l'Académie Royale des Sciences de Paris, organisaient de grandes campagnes astrogéodésiques et gravimétriques à travers le monde, dans le but de déterminer l'aplatissement de la Terre et de vérifier la théorie de Newton. Bien sûr, la Science ne fut pas l'apanage des seuls Français. Ainsi, l'an 1700 vit la fondation de l'Académie Royale des Sciences de Prusse à Berlin, et l'an 1725, la création de l'Académie Impériale des Sciences de Russie à Saint-Pétersbourg. De même que l'Académie des Sciences de Paris et la Société Royale de Londres, ces institutions vont jouer un rôle très important dans la suite pour faire progresser les connaissances scientifiques. Entretemps, Newton et Leibniz (1646–1716) avaient inventé le calcul différentiel et intégral (calcul des fluxions), lequel fut développé notamment par Jacques Bernoulli (1654–1705) et son frère Jean Bernoulli (1667–1748), par le marquis Guillaume de L'Hospital (1661–1704), par James Gregory (1638–1675) et par bien d'autres.