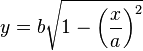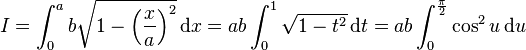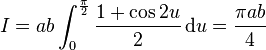Ellipse (mathématiques) - Définition
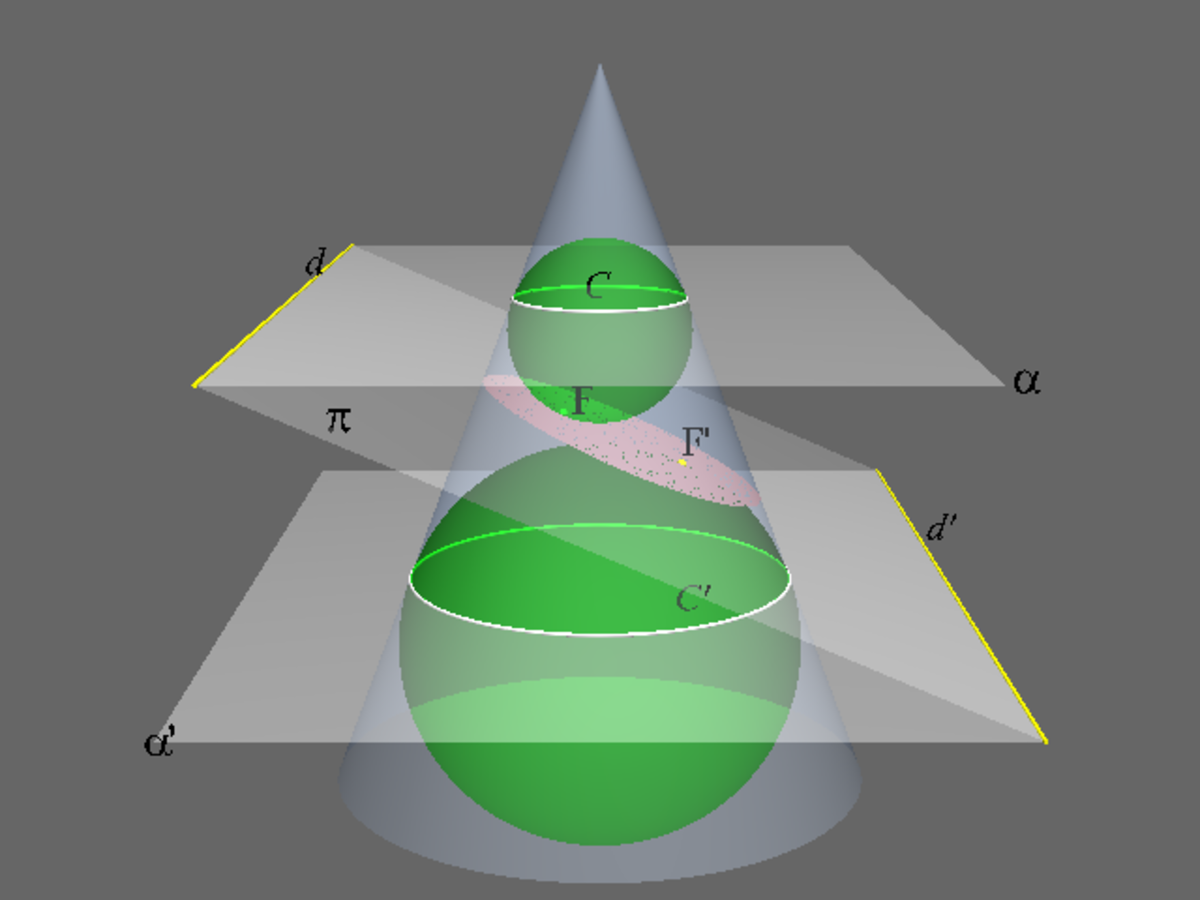
Une ellipse est, en mathématiques, une courbe plane fermée obtenue par la projection d’un cercle sur un plan sécant, ou par l’intersection d’un cône droit avec un plan non perpendiculaire à son axe. Le cercle est considéré comme un cas particulier d’ellipse.
C’est donc la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane.
En géométrie, elle est le lieu dont chacun des points est tel que la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple).
Les trajectoires des corps célestes (planètes, comètes ou satellites artificiels) en orbite autour d'une étoile ou d’une autre planète sont des ellipses en première approximation (voir problème à deux corps et problème à N corps).
Une ellipse est une conique d'excentricité strictement comprise entre 0 et 1.
Définitions géométriques
Section d’un cône
L’ellipse est une courbe plane qui fait partie de la famille des coniques. Elle est obtenue par l’intersection d'un plan avec un cône de révolution lorsque ce plan traverse de part en part le cône. Le cercle est alors un cas particulier de l'ellipse (plan de coupe perpendiculaire).
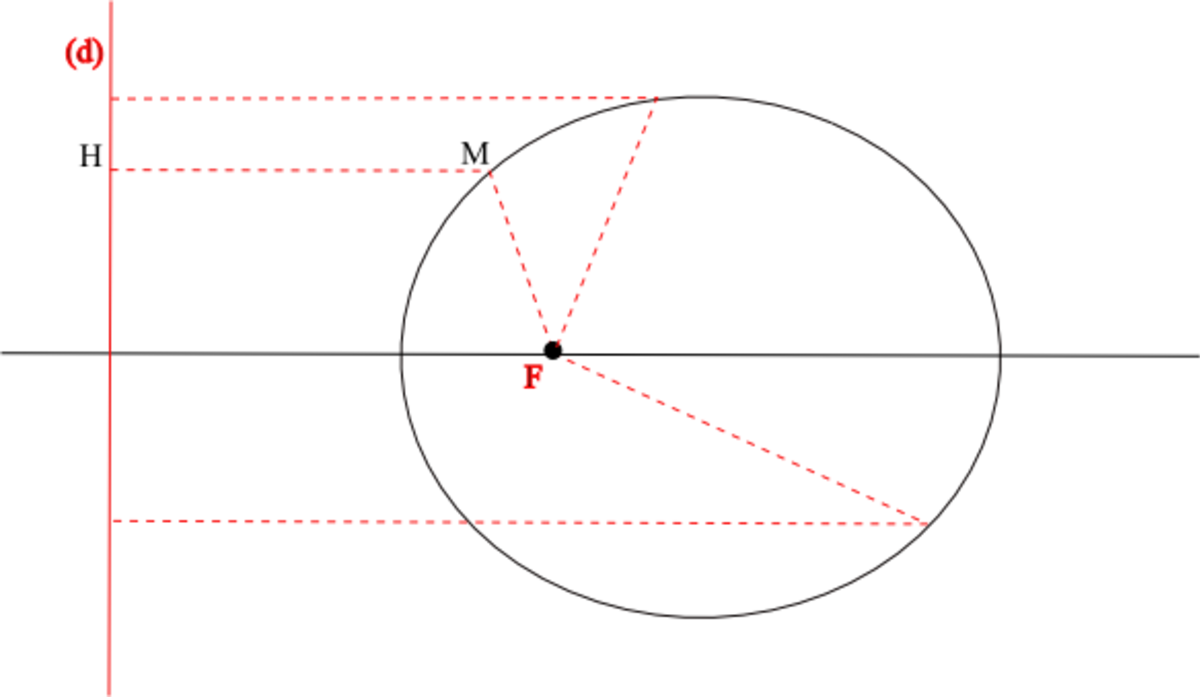
Directrice et foyer
Le cadre est l'espace affine euclidien de dimension 2. Soient (d) une droite, F un point n'appartenant pas à (d), e un réel dans ]0,1[. Soit P le plan affine déterminé par (d) et F. On appelle ellipse de droite directrice (d), de foyer F d'excentricité e l'ensemble des points M du plan P vérifiant :
où d(M,F) mesure la distance du point M au point F et d(M,(d)) = d(M,H) celle de M à la droite (d).
Notons K le projeté orthogonal de F sur (d). (KF) est alors clairement un axe de symétrie de l'ellipse appelé axe focal.
Définition bifocale de l'ellipse
Soient F et F' deux points distincts du plan. On appelle ellipse de foyers F et F', l'ensemble des points M du plan vérifiant la propriété suivante :
où 2a est la longueur du grand axe, 2c = d(F,F') et 2b est la longueur du petit axe (perpendiculaire au grand axe).
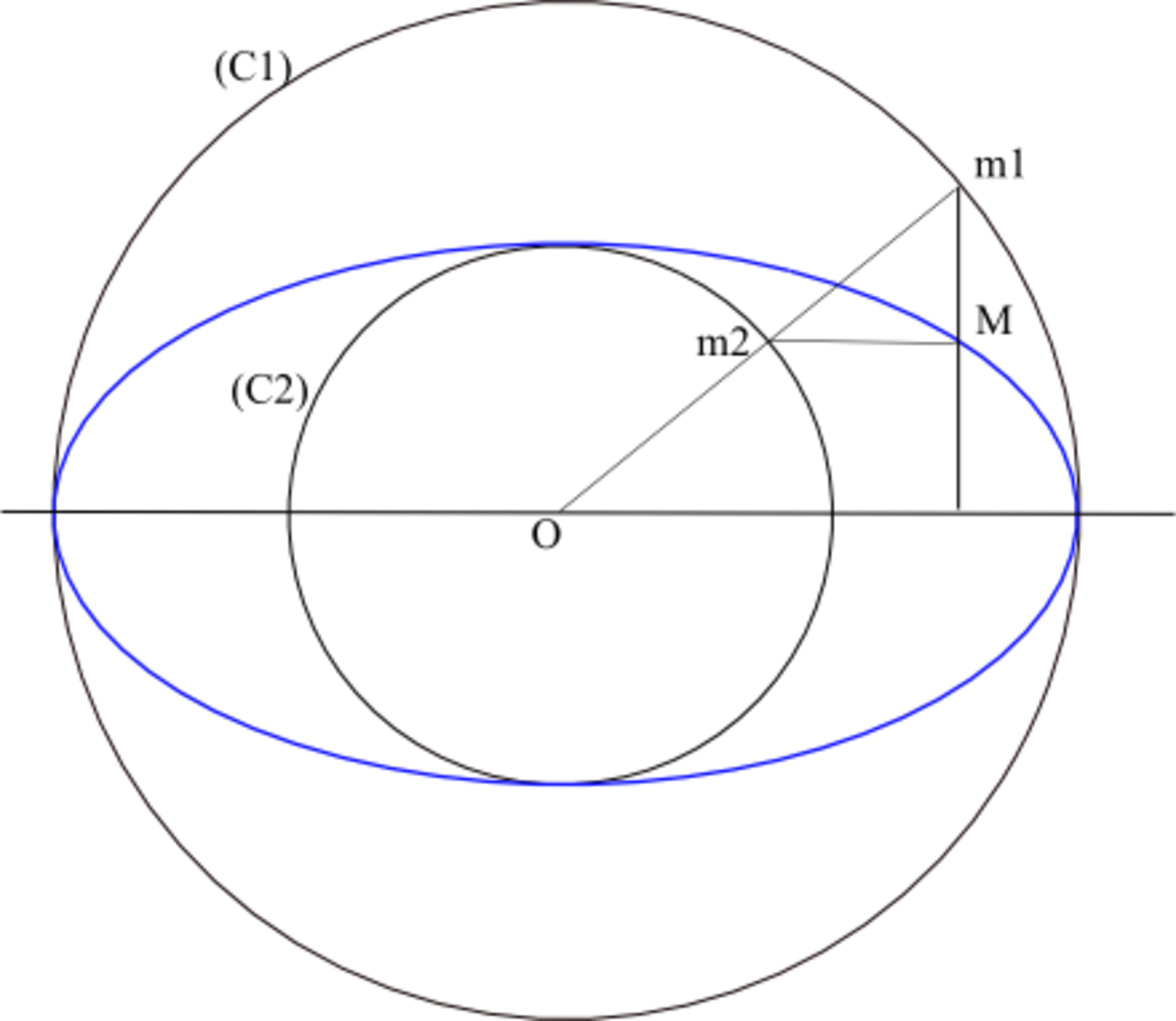
Image d'un cercle par une affinité
Soient (C1) un cercle de centre O et de rayon a, (C2) un cercle de centre O et de rayon b (b < a) et (xx') une droite passant par O. On appelle ellipse de centre O, de demi-grand axe a et de demi-petit axe b l'image du cercle (C1) par l'affinité d'axe (xx'), de direction perpendiculaire à (xx') et de rapport b /a.
Pour construire le point M de l'ellipse, image du point m1 du grand cercle, on construit le point m2 du cercle (C2) situé sur [Om1]. On mène par m1 une perpendiculaire à (xx') et par m2 une parallèle à (xx'). Les droites se coupent en M. En effet, si m' est le projeté orthogonal de m1 sur (xx'), on a, d'après le théorème de Thalès,
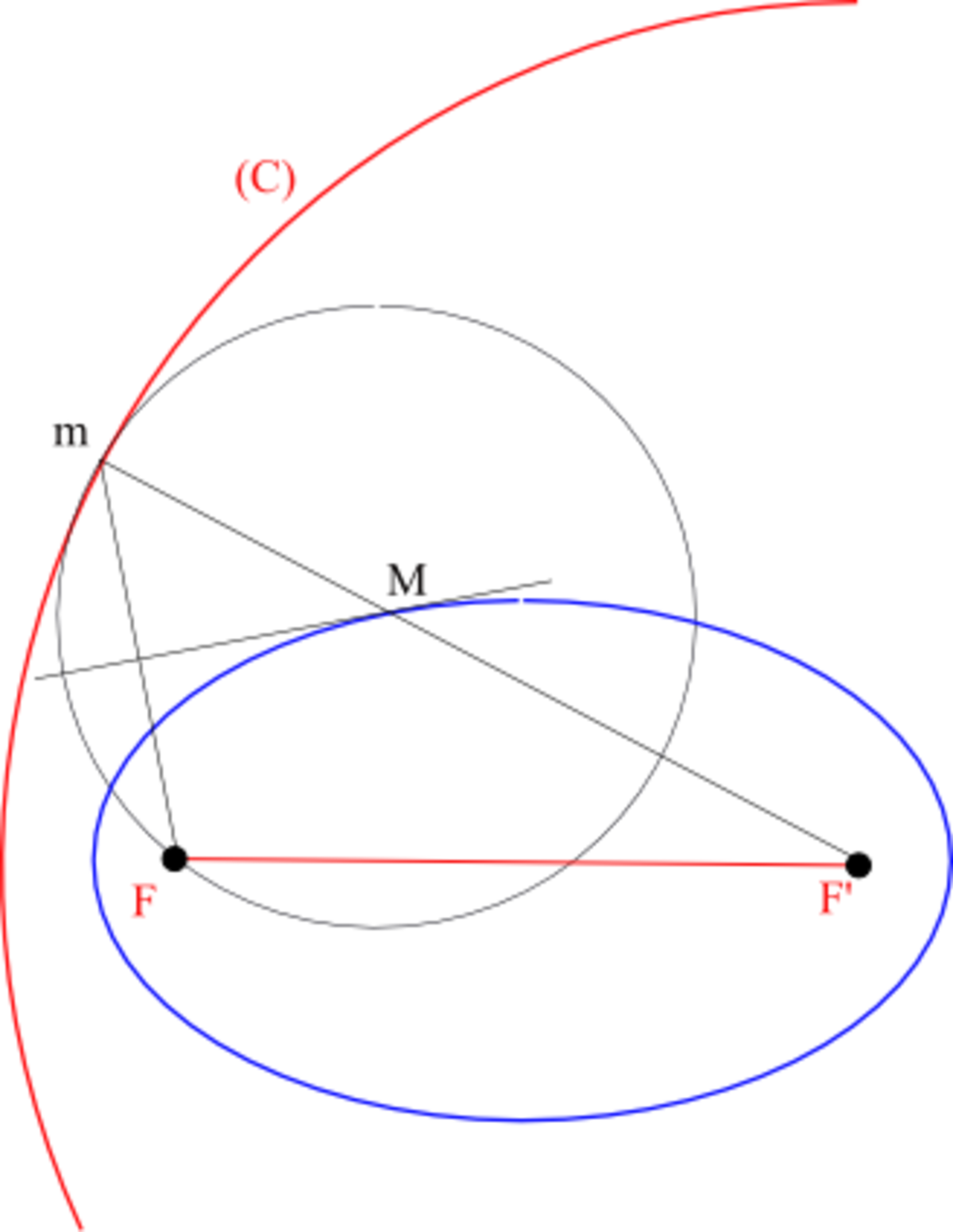
Construction par le cercle directeur
Soient F et F' deux point distincts, (C) un cercle de centre F' et de rayon 2a (2a > FF').
On appelle ellipse de cercle directeur (C) et de foyer F, l'ensemble des centres des cercles tangents à (C) et passant par F.
Pour construire le point M, centre du cercle tangent à (C) en m, on trace la médiatrice du segment [Fm], elle rencontre le rayon [F'm] en M.
Propriétés géométriques
Éléments de symétrie
L'" axe focal ", aussi appelé " grand axe ", passant par le foyer et perpendiculaire à la directrice, est axe de symétrie de l'ellipse; de même pour le petit axe, perpendiculaire au grand axe et passant par le "centre de l'ellipse", milieu de [FF']. L'intersection du grand axe et du petit axe, centre de l'ellipse, est un centre de symétrie.
Les points d'intersection de l'ellipse avec son grand axe sont appelés sommets principaux, ceux de l'ellipse avec son petit axe sont dits secondaires.
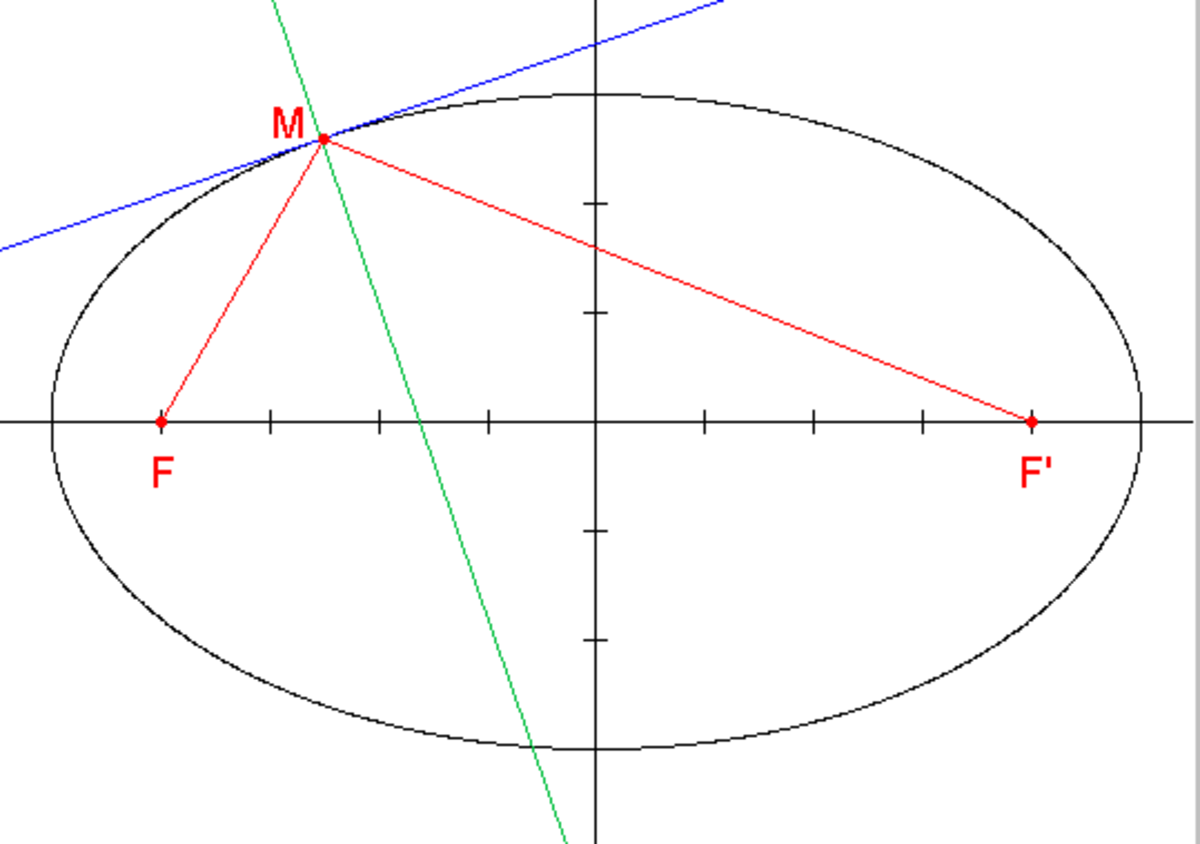
Tangente et bissectrice
Soit une ellipse dont les foyers sont F et F'. En un point M de cette ellipse, considérons la bissectrice du secteur angulaire(FMF'). Alors, cette bissectrice est perpendiculaire à la tangente en M.
Cette propriété est utilisée en optique géométrique dans les miroirs elliptiques : un rayon lumineux qui passe par un des foyer, lorsqu'il est réfléchi, passe par l'autre foyer. Ainsi, si l'on met une ampoule à un foyer d'un miroir elliptique, le faisceau lumineux se concentre sur l'autre foyer.
Ceci explique également le fait que les sons se propagent très bien d'un quai à l'autre du métro parisien. En effet, la plupart des stations ont une forme elliptique. Si la source d'un son se trouve à un des foyers, tous les sons réfléchis vont converger vers l'autre foyer (sur l'autre quai). Cette propriété possédée par l'ellipse est aussi appelée " propriété de réflexivité " et s'explique en se servant de la tangente en un point de l'ellipse: de cette façon, un son ou un rayon lumineux émis d'un des foyers sera réfléchi sur l'autre foyer. Cette propriété est exploitée dans la conception de certains instruments d'optique. Elle est évidemment présente dans une galerie à écho, c'est-à-dire dans une pièce dont le plafond, par sa forme elliptique, fait qu'une personne qui chuchote en l'un des foyers est entendue en l'autre foyer. La rotonde du Capital Building à Washington et le Mormon Tabernacle à Salt Lake City sont des exemples de cette sorte de galerie. (Extrait du livre d'Analyse 5e édition, de SWOKOWSKI, traduit de l'anglais par Micheline Citta).
Rapport entre les grandeurs
Si l'ellipse est définie par son excentricité e et la distance h entre le foyer et la directrice, alors
- p = eh où p est le paramètre de l'ellipse.
-
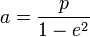
-
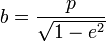
-
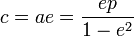
Si l'ellipse est donnée par ses demi-axes a et b
-
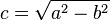
-
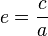
-
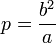
-
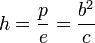
Équations caractéristiques
Équation cartésienne
Dans le repère défini par le grand axe et le petit axe de l'ellipse, son équation est:
Si une ellipse n'est pas centrée à l'origine d'un système de coordonnées x-y, mais que son grand axe et son petit axe restent parallèles aux axes des coordonnées, celle-ci peut être spécifiée par l'équation suivante:
où les paramètres h et k sont les coordonnées du centre de l'ellipse.
Paramétrisation
dans le repère défini par le grand axe et le petit axe.
Équation polaire
dans le repère défini par le foyer et l'axe focal.
ou
dans le repère défini par le centre et l'axe focal.
Circonférence
La circonférence d'une ellipse est 4aE(e), ou E est une intégrale elliptique complète de deuxième espèce.
La série est :
Une bonne approximation est donnée par une formule de Ramanujan :
qui peut aussi s'écrire :
ou a est la demi-longueur du grand axe et b la demi-longueur du petit axe.
Plus généralement, la longueur de l'arc, comme une fonction de l'angle sous-tendu, est donnée par une intégrale elliptique incomplète de seconde espèce. La fonction réciproque, l'angle sous-tendu comme une fonction de la longueur de l'arc, est donnée par les fonctions elliptiques.
Aire du domaine intérieur à une ellipse
Il existe différentes manières de calculer l'aire d'une ellipse. On peut se placer dans le repère porté par les axes où l'équation de l'ellipse s'écrit :
Avec les symétries établies plus haut, il suffit de calculer par exemple l'aire de la portion d'ellipse dans le quart supérieur droit du plan rapporté à ce repère. L'équation de la portion d'ellipse correspondante est :
pour x dans [0,a]. D'où l'aire du quart supérieur droit d'ellipse :
la dernière réécriture obtenue avec le changement de variable
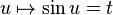
et pour l'aire de toute l'ellipse :
- S = πab
Remarquer que pour a = b, on retrouve l'aire du cercle.
Tracer une ellipse
- Méthode des deux points et de la corde : selon la propriété (lien), la somme AF + AF' des distances entre un point A de l'ellipse et ses deux foyers F et F' est constante. Ainsi, on plante deux piquets dans le sol (les deux foyers), on prend une corde non élastique de longueur donnée (la somme constante) que l'on attache aux piquets; le trajet que l'on parcourt en maintenant la corde tendue est une ellipse. On nomme cette technique celle de " l'ellipse du jardinier ".
Tracé d'une ellipse à l'aide de deux piquets et d'une corde non élastique tendue
- En dessin industriel, une ellipse est en général un cercle vu en perspective (une pièce est rarement elliptique même si ce n'est pas exclu), ou bien un perçage en biais par rapport à la surface de la pièce. L'ellipse se représente donc avec les même traits d'axe que pour le cercle. Dans le cas d'un cercle vu en perspective, ces traits d'axe sont inclinés et suivent les directions de référence. Dans le cas d'une forme réellement elliptique, les traits d'axes sont perpendiculaires.
Ellipse servant à représenter un perçage droit vu en perspective (figure de droite); le trait d'axe vertical figure l'axe du perçage
Ellipse servant à représenter un perçage oblique vu de face (figure de droite)
- Tracé à main levée, méthode du parallélogramme exinscrit : on a vu ci-dessus qu'une ellipse pouvait être considérée comme un cercle vu en perspective. De même qu'un cercle est inscrit dans un carré, une ellipse est inscrite dans un parallélogramme qui n'est autre que ce carré vu en perspective cavalière (notez qu'il existe une infinité de parallélogrammes exinscrits, il suffit d'en choisir un). On trace d'abord un parallélogramme, on le divise en quatre quartiers selon les parallèles aux côtés passant par les milieux des autres côtés; dans chaque quartier, on trace un arc passant par les milieux des côtés et tangent aux côtés en ces milieux.
Tracé d'une ellipse à main levée à l'aide d'un parallélogramme
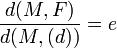
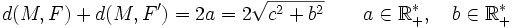
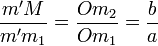
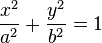
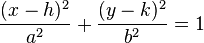
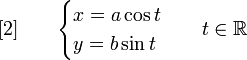
![[3a] \qquad r = \frac{p}{1+e \cos \theta} \qquad \theta \in\R](https://static.techno-science.net/illustration/Definitions/autres/d/d86daee13a72681f39bc900b81f29614_6318910115a918b956c899b3888177b6.png)
![[3b] \qquad r^2 = \frac{b^2}{1-e^2 \cos ^2 \theta} \qquad \theta \in\R](https://static.techno-science.net/illustration/Definitions/autres/2/2f63c552693a4c082587efe35985a268_54e1fdeda3174c003fb6f9f0c3416f1c.png)
![c = 2\pi a \left[{1 - \left({1\over 2}\right)^2e^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{e^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{e^6\over5} - \dots}\right]](https://static.techno-science.net/illustration/Definitions/autres/5/5f685ae0bd8cfe8e222e21c1e0235ed5_9aef099ec801062a8bd48890b0f4908c.png)
![c \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]](https://static.techno-science.net/illustration/Definitions/autres/a/aed48da661e7dde46dd3f629b93d8f13_a14995b052890d01df9c1fe3b46b388c.png)
![c \approx \pi a \left[ 3 (1+\sqrt{1-e^2}) - \sqrt{(3+ \sqrt{1-e^2})(1+3 \sqrt{1-e^2})} \right]](https://static.techno-science.net/illustration/Definitions/autres/d/de161dbd0cf20681d2d065c646fdc954_57e77c62a4bdaaeaca753cb6354cd93f.png)