Effet de peau - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'effet de peau ou effet pelliculaire (ou plus rarement effet Kelvin) est un phénomène électromagnétique qui fait que, à fréquence élevée, le courant a tendance à ne circuler qu'en surface des conducteurs.
Effet de peau pour un conducteur isolé
Ce phénomène d'origine électromagnétique existe pour tous les conducteurs parcourus par des courants alternatifs. Il provoque la décroissance de la densité de courant à mesure que l'on s'éloigne de la périphérie du conducteur. Il en résulte une augmentation de la résistance du conducteur.
Cela signifie que le courant ne circule pas uniformément dans toute la section du conducteur. Tout se passe comme si la section utile du câble était plus petite. La résistance augmente donc, ce qui conduit à des pertes par effet joule plus importantes.
Effet de peau entre deux conducteurs
Dans un câble composé de deux conducteurs (aller et retour du courant), à haute fréquence il peut se produire un effet de proximité entre les deux conducteurs, improprement confondu avec l'effet de peau, qui fait que le courant a tendance à circuler seulement sur les parties des conducteurs en vis à vis.
Cet effet s'ajoute à l'effet de peau proprement dit. Il est totalement dépendant de la géométrie de l'ensemble : section des conducteurs (circulaire, carrée, plate...), distance entre conducteurs, asymétrie des conducteurs (par exemple fil parallèle à un plan de masse), etc. L'effet de proximité est pratiquement négligeable sur des conducteurs espacés de plus de 20 cm.
Afin d'atténuer cet effet, il faut éloigner les conducteurs, mais cela a d'autres inconvénients, comme d'augmenter l'inductance.
Mise en évidence de l'effet de peau par Nikola Tesla
Sur son estrade, Nikola Tesla avait des bobinages, des lampes à incandescences, et surtout, d'étonnants tubes de verre emplis de gaz à très basse pression. Tesla saisissait d'une main un fil conducteur provenant d'une de ses bobines, et où circulait un courant alternatif à haute tension. De l'autre main, il prenait un tube et celui-ci s'illuminait, à la stupéfaction de la salle !
Le secret ? Tesla employait un courant à très haute fréquence. Par "effet de peau", celui-ci ne pénètre pas dans les conducteurs, comme le corps humain, mais circule à leur périphérie.
Épaisseur de peau dans un métal
L'épaisseur de peau détermine, en première approximation, la largeur de la zone où se concentre le courant dans un conducteur. Elle permet de calculer la résistance effective à une fréquence donnée. Dans ce calcul, on néglige la partie réelle devant la partie imaginaire : la conductivité des métaux étant très élevée.
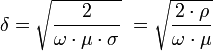
- δ : épaisseur de peau en mètre [m]
- ω : pulsation en radian par seconde [rad/s] (ω=2.π.f)
- f : fréquence du courant en Hertz [Hz]
- µ : perméabilité magnétique en Henry par mètre [H/m]
- ρ : résistivité en Ohm-mètre [Ω.m] (ρ=1/σ)
- σ : conductivité électrique en Siemens par mètre [S/m]
Pour un conducteur de section significativement plus grande que δ, on peut calculer la résistance effective à une fréquence donnée en considérant que seule la partie extérieure d'épaisseur δ contribue à la conduction. Par exemple pour un conducteur cylindique de rayon R, on aura une section utile de :
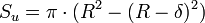
Exemples de valeurs
Pour un conducteur en cuivre, on a les valeurs ci-dessous.
| fréquence | δ |
|---|---|
| 50 Hz | 9,38 mm |
| 60 Hz | 8.57 mm |
| 10 kHz | 0.66 mm |
| 100 kHz | 0.21 mm |
| 1 MHz | 66 µm |
| 10 MHz | 21 µm |
Modélisation de l'effet pelliculaire dans un conducteur cylindrique en régime harmonique
Soit I(r) le courant circulant dans l'épaisseur comprise entre la surface et le rayon r du cylindre, et I le courant total.
La fonction de répartition du courant ayant pour origine r = 0 la surface du conducteur est donnée par l'expression :
|
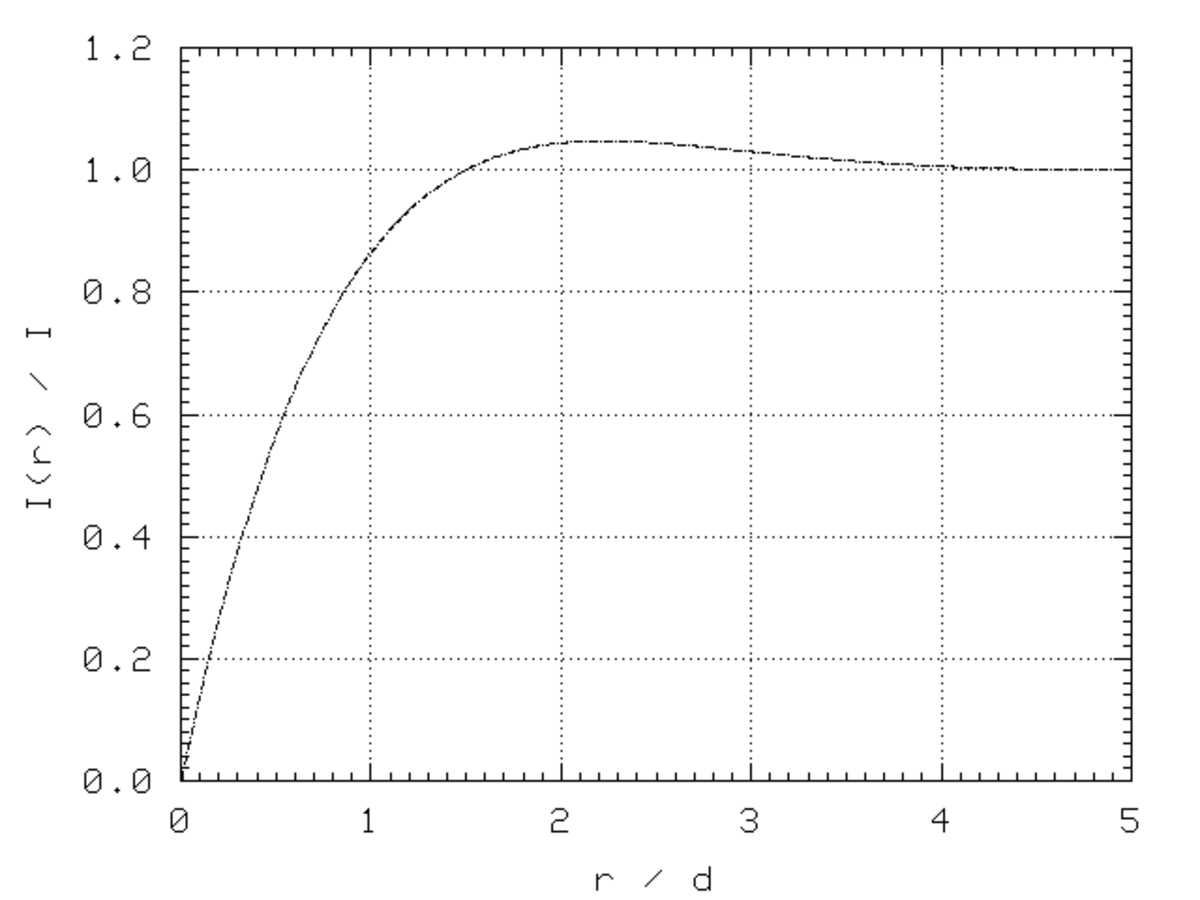
Si l'on représente graphiquement le module de la fonction de répartition du courant dans le conducteur cylindrique, c’est-à-dire
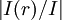
On considère un cylindre de rayon a et de longueur infinie. On se place en régime harmonique, le cylindre étant parcouru par un courant alternatif sinusoïdal de pulsation ω. L'étude en régime harmonique se fait en prenant la transformée de Fourier des équations de Maxwell.
L'équation de Maxwell-Faraday en régime harmonique s'écrit :
L'équation de Maxwell-Ampère s'écrit :
dans lesquelles
- E est le vecteur champ électrique
- B est le vecteur induction magnétique
- H est le vecteur champ magnétique
- J est le vecteur densité de courant
Il faut adjoindre à ces équations la loi de magnétisation du matériau
μ étant la perméabilité magnétique absolue du matériau, ainsi que la loi d'Ohm dans le conducteur, sous sa forme locale :
σ étant la conductivité électrique du matériau.
Faisant l'hypothèse que le conducteur est homogène, ces deux paramètres μ et σ sont constant dans le matériau, ce qui permet de multiplier l'équation de Maxwell-Faraday par la conductivité électrique
et de même, l'équation de Maxwell-Ampère peut être multipliée par la perméabilité magnétique
On se place dans un système de coordonnées cylindriques dont les variables seront notées (r, θ, z), z étant l'axe de symétrie du cylindre.
Dans ce système de coordonnées on fait les hypothèses suivantes sur la densité de courant :
- le vecteur densité de courant est dirigé suivant l'axe du cylindre
- la densité de courant ne varie pas suivant l'axe du cylindre
- la densité de courant est parfaitement axisymétrique, elle ne dépend donc pas de l'angle θ.
Ces hypothèses amènent à écrire le vecteur densité de courant sous la forme suivante :
Si l'on prend le rotationnel de l'équation de Maxwell-Faraday, on trouve :
soit, en utilisant une relation d'analyse vectorielle
Étant donnée les hypothèses faites sur le vecteur densité de courant, on a
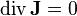
En coordonnées cylindriques, la composante axiale du Laplacien s'écrit :
En posant
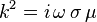
Si l'on effectue le changement de variable
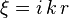
Afin d'assurer la continuité du courant en r = 0, on recherche des solutions de cette équation sous la forme J0(ξ), J0 étant la fonction de Bessel de première espèce d'ordre 0. Ainsi, on aura :
j0 étant une constante. On peut par ailleurs détailler la constante k
δ étant l'épaisseur de peau précédemment définie par
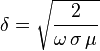
et de même
et donc, finalement, la densité de courant est donnée par
ber et bei étant les fonctions de Kelvin-Bessel d'ordre zéro.
Le courant total à travers la section est alors défini par :
Notons Ber et Bei les primitives suivantes, qui peuvent s'évaluer au moyen d'une série :
Avec ces notations, on peut alors exprimer le courant total sous une forme plus compacte
On peut calculer de même le courant circulant dans l'épaisseur comprise entre la surface et le rayon r :
et donc finalement la fonction de répartition du courant ayant pour origine r=0 la surface du conducteur est donnée par l'expression suivante :
Atténuation de l'effet de peau
L'effet de peau est généralement une nuisance, car il crée des pertes supplémentaires, des atténuations à fréquence élevée, etc. Une manière efficace d'en diminuer l'effet est de diviser le conducteur, c'est-à-dire de le remplacer par plusieurs conducteurs en parallèle isolés entre eux.
Dans l'idéal, chaque « brin » du conducteur ainsi formé devrait avoir un rayon inférieur à δ. Le fil de Litz est un type de conducteur qui pousse à l'extrême cette division.
Une autre technique consiste à plaquer le conducteur avec de l'argent. Lorsque la «peau» est entièrement dans la couche d'argent, elle bénéficie de ce que l'argent a la plus faible résistivité de tous les métaux. Cette méthode peut être un bon compromis pour un courant composé de deux composantes, l'une à basse fréquence qui circulera dans la totalité de la section, l'autre à très haute fréquence qui circulera dans l'argent.
On peut enfin envisager des géométries de conducteurs permettant de limiter l'effet de peau. Dans les postes électriques haute tension, on utilise fréquemment des conducteurs tubulaires creux en aluminium ou cuivre pour transporter de forts courants. L'épaisseur du tube est en général de l'ordre de δ, ce qui permet une utilisation effective de l'ensemble du conducteur. En basse tension on utilise parfois des géométries plus complexes et permettant un meilleur comportement thermique, mais l'idée est toujours d'avoir des épaisseurs de conducteur ne dépassant pas δ.
![\frac{I(r)}{I} = \frac{Ber(\frac{\sqrt{2}\,a}{\delta})-Ber(\frac{\sqrt{2}\,r}{\delta}) + i \, [Bei(\frac{\sqrt{2}\,a}{\delta}) - Bei(\frac{\sqrt{2}\,r}{\delta})]}{Ber(\frac{\sqrt{2}\,a}{\delta}) + i \, Bei(\frac{\sqrt{2}\,a}{\delta})}](https://static.techno-science.net/illustration/Definitions/autres/3/3f32c783bcaef4acfd113f8032bc1d40_30385cb810c6838495aa447fa34cd467.png)
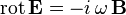
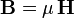
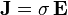
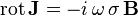
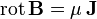
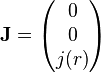
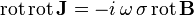
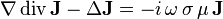
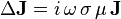
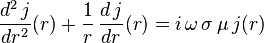
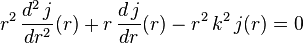
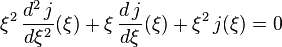
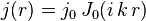
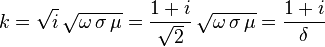
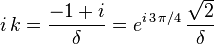
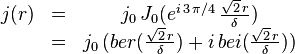
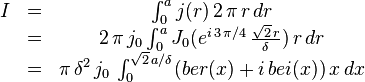
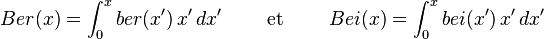
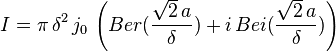
![\begin{matrix}I(r) &=& \int_{a-r}^a j(r^\prime) \, 2 \, \pi \, r^\prime \, dr^\prime\\ &=& \pi \, \delta^2 \, j_0 \, \left( Ber(\frac{\sqrt{2}\, a}{\delta})- Ber(\frac{\sqrt{2}\, r}{\delta}) + i \, [Bei(\frac{\sqrt{2}\, a}{\delta}) - Bei(\frac{\sqrt{2}\, r}{\delta})] \right)\end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/c/c659bbada4519b05cb22ef4023921c09_7ddef5a13e6d523068b0505a8ac75019.png)

















































