Équation - Définition

Analyse

Zéro d'une fonction

La dichotomie		Le théorème du point fixe		La méthode de Newton.

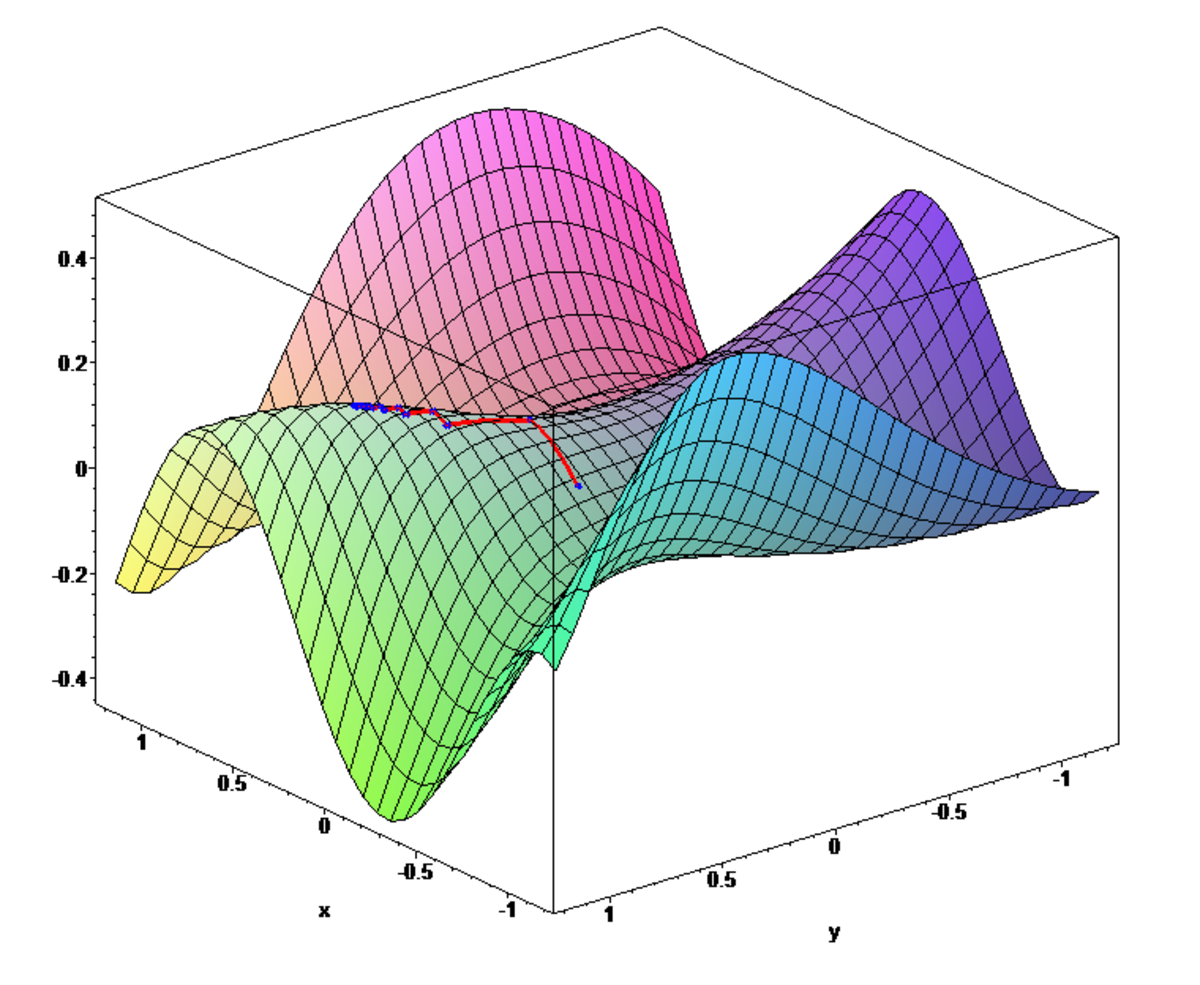
En analyse plus encore, il sera bien souvent vain d'espérer traiter une équation par des techniques élémentaires de substitution ou transformation, en espérant isoler la variable. Et même quand cela s'avère possible, comme pour certaines équations algébriques, si l'objectif est l'obtention d'une valeur numérique, l'approche décrite dans ce paragraphe est souvent moins coûteuse. On peut toujours ramener l'équation à une forme f(x) = 0. Considérons par exemple l'équation suivante, l'inconnue étant un réel strictement positif :

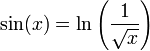
Elle se réécrit f(x) = 0 si on pose f(x) = sin(x) + 1/2ln(x). Un zéro est une solution de l'équation dans ce cas particulier. Il serait vain de chercher à exprimer un zéro par une formule composant des fonctions élémentaires (fractions rationnelles, fonctions exponentielles, logarithmiques ou trigonométriques...). Une telle expression n'existe pas ici. On se contentera de chercher le nombre de zéros, des intervalles les contenant, ainsi que des approximations de ces zéros.

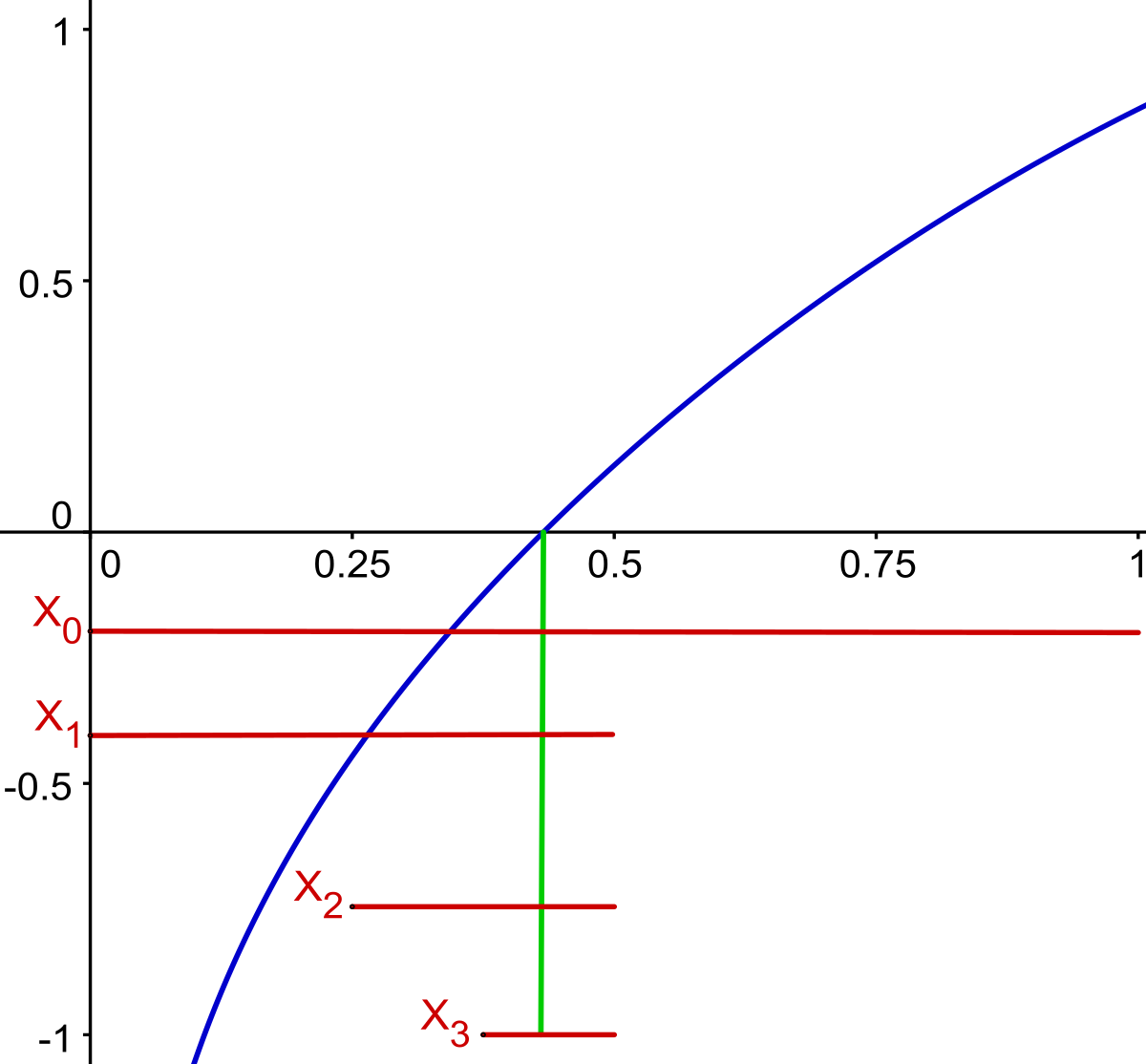
Dans l'exemple, l'étude de la fonction f montre facilement qu'il y a exactement trois zéros, un dans l'intervalle ]0, 1], un dans [3, 4] et le dernier dans [5, 6]. La continuité de f permet de construire une première suite (x_n) convergeant vers le zéro de l'intervalle ]0, 1]. Au voisinage de 0, la fonction est strictement négative, au point 1, elle est strictement positive, le théorème des valeurs intermédiaires garantit l'existence d'un zéro dans cet intervalle, car f est continue. On pose x₀ = 0, au point 1/2, la fonction f est strictement positive, on en déduit l'existence d'un zéro dans l'intervalle [0, 1/2] et on pose x₁ = 0. Au point 1/4, elle est strictement négative, on en déduit l'existence d'un zéro dans [1/4, 2/4] et on pose x₂ = 1/4 et ainsi de suite. On construit ainsi une suite convergeant vers la solution, ce qui permet d'obtenir une approximation aussi précise que souhaitée. Cette méthode porte le nom de dichotomie et est la première illustrée dans la figure du paragraphe.

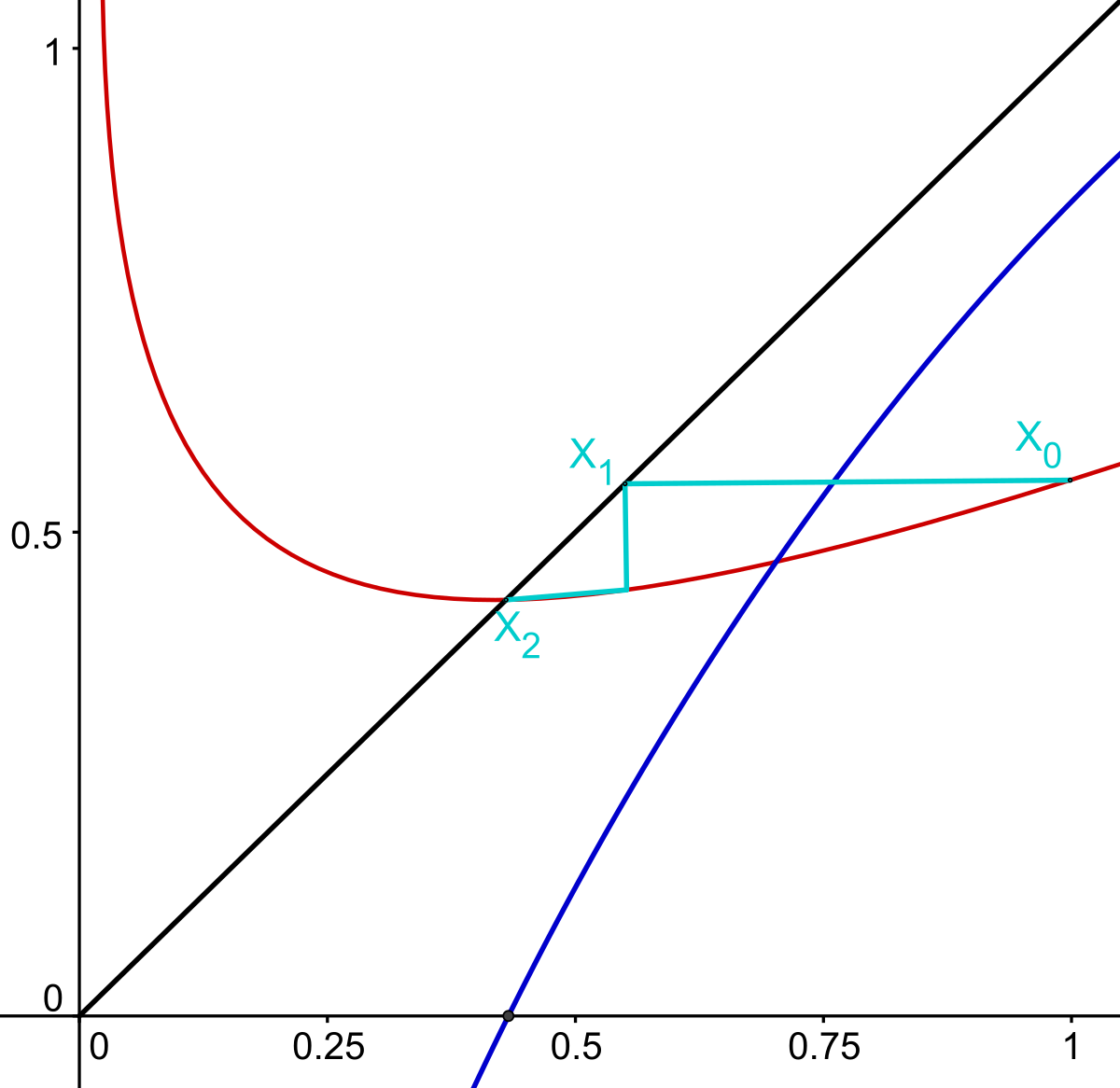
Seule la continuité de f a été utilisée dans l'algorithme précédent, un théorème du point fixe est à la base d'une méthode plus efficace. On construit une fonction g (en rouge sur la figure du milieu) ayant pour point fixe (c'est-à-dire un point x tel que g(x) = x) la solution recherchée. On choisit g de telle manière à ce que la dérivée au point fixe soit la plus petite possible. Une solution simple est de définir g(x) = x + λ.f(x). Dans l'exemple, on peut choisir λ égal à -1/2. Cette fois-ci, il est plus judicieux de choisir x₀ égal à 1. On définit x_n = g(x_n-1). Si la dérivée de g est proche de 0, la convergence est bien meilleure que celle de l'algorithme précédent. Dans l'exemple choisi, la solution est égale à 0,43247... La quatrième itération de la première méthode donne pour valeur 0,375 alors que celle issue du point fixe donne 0,4322...

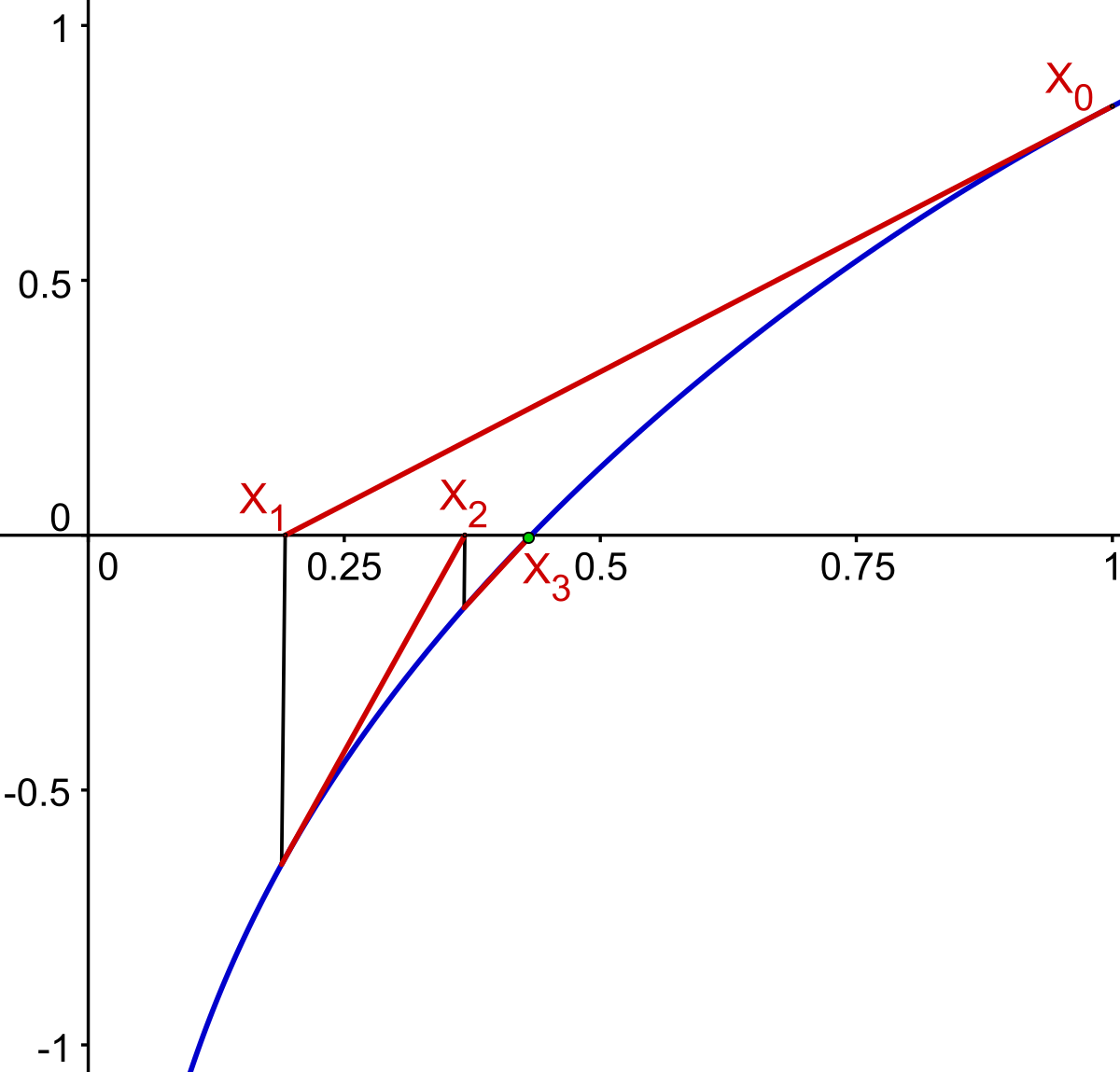
La dérivabilité de f partout sur son domaine permet la mise au point d'un algorithme ayant une convergence encore meilleure. La méthode consiste, à partir d'un point x₀, égal à 1 dans l'exemple, à trouver la solution x₁ de l'équation linéaire tangente de la fonction f au point x₀. Puis on construit x₂ comme la solution de l'équation linéaire tangente de la fonction f au point x₁. Dans l'exemple étudié, illustré sur la figure de droite, la valeur de x₄ est égale à 0,43246 soit quatre décimales exactes. Cette méthode porte le nom de Newton.

Équation vectorielle

La méthode de descente du gradient s'applique à toute équation d'un espace vectoriel de dimension finie et à valeurs dans l'ensemble des nombres réels. Elle est illustrée ici à l'aide d'une représentation en courbes de niveaux

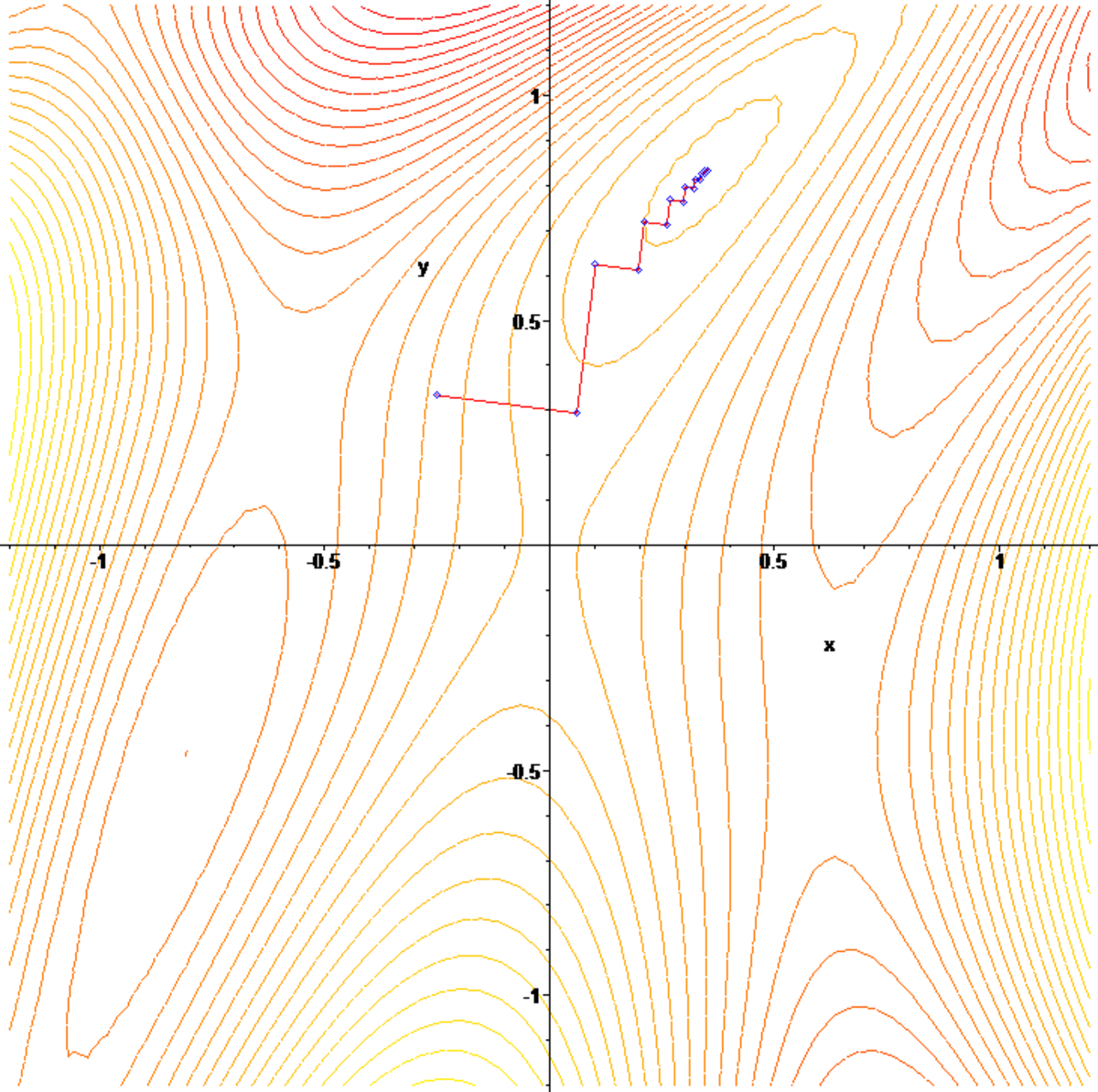
Si l'équation prend la forme f(x) = 0 où f est une fonction d'un espace vectoriel E à valeurs dans un espace vectoriel F dont le vecteur nul est noté 0, les idées de l'algèbre linéaire peuvent encore s'appliquer partiellement. Il est possible de choisir une base de E et de F et d'exprimer f à l'aide de m fonctions f_j réelles de n variables x_k, où m est la dimension de F et n celle de E, on obtient ce que l'on appelle un système d'équations, de la forme suivante :

Cette représentation correspond à la même équation que celle représentée à gauche, mais cette fois-ci en dimension 3.

Les mêmes limitations que celles décrites au paragraphe précédent s'appliquent. Il est tout à fait possible que la technique d'isolation des variables, qui fonctionne dans le cas de l'équation linéaire, ne soit pas possible, par exemple si les f_i contiennent des expressions trop complexes. Certaines des idées, exprimées dans le cas où f est une fonction de la variable réelle à valeurs réelles, peuvent s'adapter à la géométrie d'un espace vectoriel de dimension finie, d'autres non. Il n'existe pas d'équivalent du théorème des valeurs intermédiaires pour la nouvelle configuration. En revanche, le théorème du point fixe se généralise, ainsi que la définition d'une dérivée.

La dérivée, ou plutôt la différentielle de f peut être utilisée de plusieurs manières. La première est une simple adaptation de la méthode de Newton, à partir d'un point x₀, on résout l'équation linéaire tangente en ce point, c'est-à-dire Df_x0.h + f(x₀) = 0. La valeur x₁ est égale à x₀ + h et l'on réitère le processus pour obtenir une suite. Si E est égal à F et pour permettre une convergence plus rapide, on résout souvent une équation linéaire analogue, mais dont l'application linéaire associée définit un produit scalaire. Cette astuce permet une accélération du temps de traitement de la résolution des équations linéaires intermédiaires, la méthode associée porte le nom de quasi-Newton.

Une autre méthode consiste à transformer l'ensemble d'arrivée en R₊, par exemple en équipant F d'un produit scalaire et en recherchant les zéros de la fonction g à valeurs réelles, qui à x associe le carré de la norme de f(x) ou encore le produit scalaire de f(x) avec x, si E est égal à F. Les deux équations f(x) = 0 et f(x)² = 0 possèdent les mêmes solutions. Le problème revient à trouver un extremum de la nouvelle fonction g. On part d'un point x₀ dans la direction de la ligne de plus grande pente, dont la direction est donnée par le gradient et on s'arrête au point x₁, le minimum de la fonction g dans la direction du gradient. Puis on réitère le calcul.

Analyse fonctionnelle

L'aérodynamisme d'un objet volant est régi par une équation qui s'étudie à l'aide de l'analyse fonctionnelle. Des outils puissants tels que l'espace de Hilbert sont nécessaire pour établir quelques théorèmes généraux.

Si l'espace vectoriel E est plus vaste et n'est plus de dimension finie, d'autres idées doivent être utilisées pour venir à bout de l'équation. Cette configuration se produit si l'inconnue x désigne une fonction. Une fois encore, il est vain de rechercher des méthodes systématiques exprimant les solutions sous la forme d'une composition de fonctions élémentaires, les cas où une telle expression existe tiennent plus de l'exception que de la règle.

Une méthode générale consiste associer à un espace de fonctions H_p, comme celui des fonctions continues définies sur un intervalle [a, b], une géométrie. Pour ce faire, on peut définir sur l'espace une distance euclidienne, c'est-à-dire définie par un produit scalaire comme celui qui, à deux fonctions f et g de H_p associe :

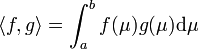
À l'aide de cette distance, on construit une suite (x_n) de fonctions qui vérifie la propriété de Cauchy, c'est-à-dire que si les indices n et m sont suffisamment grands x_n et x_m sont arbitrairement proches. Un exemple est donnée par l'équation intégrale, dite de Fredholm :

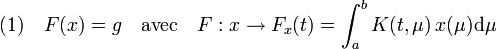
La suite (x_n) est construite de telle manière à ce que la distance entre les fonctions F_xn(t) et g(t) tende vers zéro. La difficulté est qu'une suite de Cauchy ne converge pas nécessairement dans H_p, ce qui revient à dire que cet espace n'est pas complet. Il est alors plongé dans un espace H qui le contient et qui lui, est complet. Un élément de H n'est plus une fonction, il peut être vue comme un élément du dual de H_p. Dans H, la suite (x_n) converge vers une limite s. Elle peut être interprétée comme une solution de l'équation (1) car la distance entre F(s) et g est nulle. Mais s n'est pas une fonction, c'est un être abstrait, élément du dual de H_p, on parle de solution faible. On montre enfin que cette être abstrait s'identifie à un élément de H_p, c'est-à-dire une à fonction qui vérifie l'équation (1), appelée solution forte