Équation - Définition

Algèbre

Théorie des équations

Le graphe du module du polynôme X⁵ - 3X + 2, montre que ce polynôme admet au moins quatre racines (la cinquième n'est pas visible sur le graphique), illustrant le théorème de d'Alembert-Gauss dans un cas particulier.

La première théorie des équations ne concerne que les équations polynomiales, c'est-à-dire de la forme P(X) = 0 où P est un polynôme. Elle est basée sur des transformations des membres de l'équation en appliquant les cinq opérations « classiques » (addition, multiplication, soustraction, division et extraction de racine) aux coefficients de l'équation comme à son inconnue.

Si le degré du polynôme est égal à 2 et si les coefficients et les solutions recherchées sont réels, alors ces méthodes permettent de trouver les solutions, encore appelées racine (cf l'article Équation du second degré). L'usage du changement de variable permet d'étendre la famille d'équations qui se résolvent, ainsi comme l'illustre l'exemple e^2x - (e^a + e^b)e^x + e^a+b = 0, en posant X = e^x. Cette méthode du changement de variable ne se limite pas aux équations algébriques.

Pour aller plus loin et résoudre l'équation cubique, c'est-à-dire du troisième degré, les mathématiciens italiens de la Renaissance découvrent la nécessité d'enrichir l'ensemble des nombres en lui adjoignant des nombres imaginaires. Cette découverte permet la résolution des équations du troisième et quatrième degré (Voir les méthodes de Cardan et Ferrari).

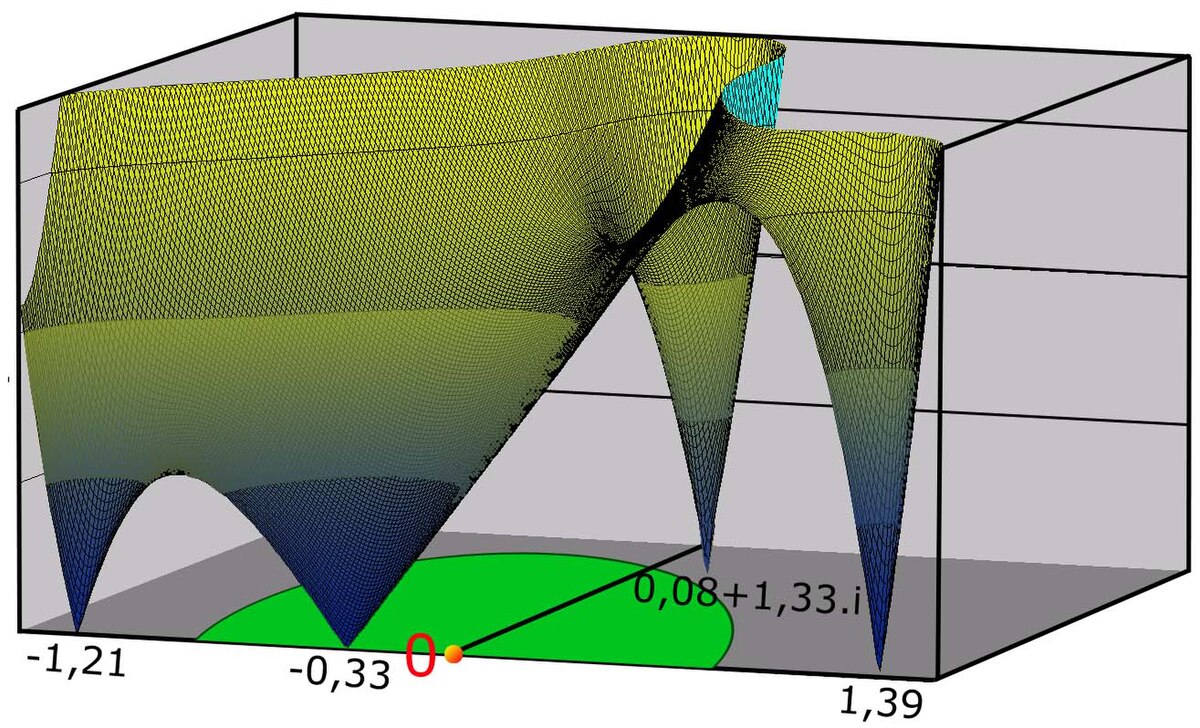
Le théorème de d'Alembert-Gauss précise que tout polynôme de degré supérieur ou égal à 1 et à coefficients réels ou complexes, admet au moins une racine complexe. Si ce théorème assure, dans un cas très général, l'existence d'une solution, il n' en offre aucune formulation explicite, et l'intuition de ces racines complexes pour les polynômes réels n'est pas immédiate. Le deuxième théorème, dit théorème d'Abel en explique la raison : il n'existe, en général, aucune formule analogue à celles qui s'appliquent aux petits degrés, capable d'exprimer les racines. Ce résultat, œuvre de Niels Abel, est complété par Évariste Galois qui indique une condition nécessaire et suffisante pour déterminer dans quels cas les racines d'une équation polynomiale possèdent une expression de cette nature. Sa démonstration fait appel à la théorie de Galois.

Les deux théorèmes précédents closent la théorie des équations. Cette expression fut encore en vigueur en mathématiques pendant tout le XIX^e siècle. Elle reste d'actualité en histoire des sciences. Elle est encore utilisée en mathématiques, mais elle est devenue rare et un peu désuète.

Système d'équations linéaires

Les Neuf Chapitres sur l'art mathématique est un livre anonyme en chinois proposant une méthode de résolution de l'équation linéaire.

Une autre famille d'équations est traitée par l'algèbre : celle des équations linéaires. Ce sont les équations de la forme (1) a(x) + b = 0, où a est une application linéaire d'un espace vectoriel E dans un espace vectoriel F, b un vecteur de F et x une variable qui décrit l'ensemble E. Si les espaces E et F sont de dimension finie, notés n pour E et m pour F, le choix d'une base de E et de F, permet d'exprimer a sous la forme d'une matrice (a_jk), x sous la forme d'un vecteur colonne à n coordonnées (x_k) et b d'un vecteur colonne à m coordonnées (b_j).

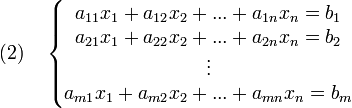
D'une équation (1) on passe à un système (2), de m équations à n inconnues. Cette technique, consistant à passer d'une équation vectorielle à un système de plusieurs équations réelles de plusieurs variables réelles, ne se limite pas au cas linéaire.

Sous la forme (2), plusieurs algorithmes permettent de trouver une racine. Si n est égal à m et si le déterminant de la matrice de a est non nul, il est possible d'utiliser la règle de Cramer. Ce n'est pas l'algorithme le plus efficace, la méthode du pivot de Gauss est plus simple et plus rapide. Elle revient à isoler les n variables à l'aide d'une suite de substitutions. Cette méthode est ancienne, on en trouve un équivalent dans le chapitre 8 du livre chinois de mathématiques intitulé Les Neuf Chapitres sur l'art mathématique et datant d'avant notre ère. Au XIII^e siècle Qin Jiushao va plus loin et trouve comment résoudre un système linéaire avec des congruences comme coefficients, pour résoudre une question liée à un « programme de répartition de grains ».

Équation linéaire et géométrie

La géométrie permet de trouver des algorithmes de résolution de l'équation linéaire, plus rapides que la méthode du pivot de Gauss. La figure illustre le graphe en dimension 3, de la fonction f.

Cette figure illustre les courbes de niveaux en bleu de la fonction f. Les segments rouges et verts correspondent au trajet suivi par la suite approximante, qui converge en deux étapes en dimension 2.

L'approche géométrique de l'équation linéaire offre des informations d'une autre nature. L'image d'une application linéaire a, c'est-à-dire l'ensemble des vecteurs qui admettent un antécédent par f forme un sous-espace vectoriel, comme l'est un plan dans un espace de dimension trois. Le noyau de a, c'est-à-dire les vecteurs de l'ensemble de départ ayant pour image le vecteur nul, est aussi un sous-espace. Ces résultats montrent que l'ensemble des solutions forme un espace affine de direction le noyau de a.

Le point de vue géométrique permet d'élaborer des algorithmes de résolution qui tiennent compte des spécificités de a. Dans certains cas particuliers, il existe des techniques qui permettent de trouver une solution plus rapidement qu'avec la méthode du pivot de Gauss. Un exemple correspond au cas où E est un espace euclidien égal à F et a est tel que l'application qui à x et y associe < -ax,y> soit un produit scalaire. Ici les crochets désignent le produit scalaire initial de l'espace E. Ceci implique que la matrice de a est de déterminant non nul et symétrique, si la base de E est choisie orthonormale.

Une méthode consiste à ne pas chercher à résoudre l'équation a.x + b = 0 mais à répondre à une autre question, d'apparence plus complexe. Elle revient à trouver le point optimal de l'expression qui à x associe f(x), défini par :

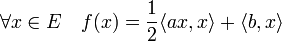
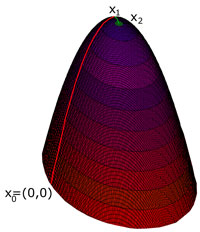
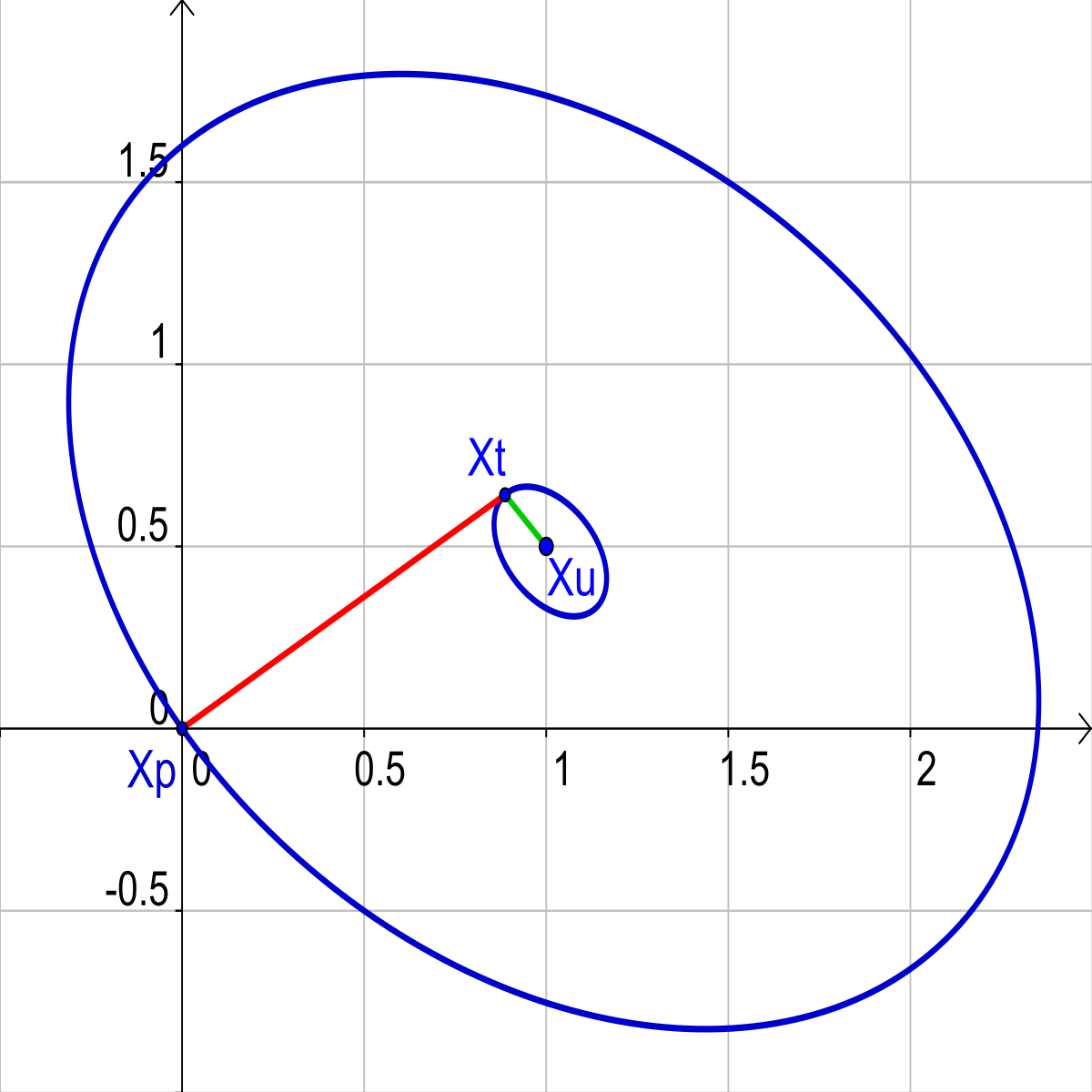
Son point optimal est la solution de l'équation linéaire. Pour comprendre la méthode de résolution, le plus simple est de représenter le cas où F est de dimension 2. Le graphe de f a alors la forme d'un pain de sucre, comme illustré sur la figure de gauche. Une méthode consiste à partir d'un point quelconque x₀ et à suivre la ligne de plus grande pente, illustrée en rouge sur les figures et qui correspond à une parabole à gauche et à un segment à droite. Le sommet de cette parabole est noté x₁. A partir du point x₁, on suit à nouveau la ligne de plus grande pente, en vert sur les figures. Cette technique porte le nom de descente de gradient.

Si, au lieu de suivre exactement le chemin de plus grande pente, on en choisit un de direction orthogonale aux directions précédentes pour le produit scalaire < -a.x,y>, la méthode converge vers la solution en un maximum de n étapes, si n désigne la dimension de E. Elle porte le nom de méthode du gradient conjugué.