Longueur d'un arc - Définition
La liste des auteurs de cet article est disponible ici.
Définition de Jordan
Motivation
Pendant 150 ans, la définition du XVIIe siècle remplit les besoins des mathématiciens, au besoin avec la généralisation de Riemann. Encore maintenant, il n'est pas rare qu'elle soit utilisée quand le sujet se limite à de la géométrie différentielle. Durant la deuxième moitié du XIXe siècle, de nouvelles questions imposent une approche plus générale.
Les courbes étudiées ne possèdent plus systématiquement une origine spécifiquement mécanique ou cinématique mais proviennent aussi d'autres branches des mathématiques. Giuseppe Peano découvre la courbe qui porte maintenant son nom et qui recouvre intégralement la surface d'un carré de côté 1. Hermann Minkowski utilise des convexes pour résoudre des questions de théorie algébrique des nombres. Les frontières de ces convexes, s'ils sont dans un plan euclidien, peuvent parfois être paramétrées comme des arcs.

Camille Jordan est un précurseur dans l'étude des courbes du plan euclidien ayant une autre origine que cinématique. Il essaie de résoudre certaines questions apparemment anodines comme celle du théorème portant son nom, ce résultat traite d'une courbe fermé et simple. Fermé signifie que l'image des extrémités du segment de définition sont confondues et simple que l'unique point double est l'extrémité. Une telle courbe sépare le plan en deux parties connexes, l'intérieur et l'extérieur de la courbe.
Pour supporter un tel développement, il est nécessaire de ne pas se limiter aux arcs géométriques de classe C1. Jordan propose une nouvelle définition de la longueur fondée sur une démarche plus proche de celle d'Archimède que des analystes du XVIIe siècle. Une méthode intuitive pour comprendre sa logique consiste à poser une corde le plus précisément possible sur l'arc que l'on désire mesurer. Pour pouvoir aisément calculer la longueur de la corde, on lui impose de suivre un trajet polygonal. On punaise les sommets de la corde sur l'arc étudié, de telle manière à ce que les punaises se succèdent, comme sur la figure de droite. En ajoutant de plus en plus de punaises, on impose à la corde de suivre de plus en plus précisément l'arc. Une fois accrochée une infinité de punaises régulièrement espacées on obtient la longueur recherchée. Si cette approche possède l'avantage d'être pertinente, même dans le cas d'un arc non dérivable, donner un sens rigoureux à l'idée d'une infinité de punaises régulièrement espacées serait un peu délicat. Jordan propose plutôt la borne supérieure des longueurs des différentes cordes imaginables, attachées avec un nombre fini de punaises. Cette démarche allie la rigueur avec une généralisation de la longueur aux arcs non nécessairement dérivables.
Par delà le fait de pouvoir traiter des courbes non dérivables, de nouvelles méthodes deviennent utilisables qui ne l'étaient pas avec la définition précédente. Un exemple est donné avec le théorème isopérimétrique. Ce théorème stipule que toute surface possède une aire plus petite que celle du disque de même périmètre. Certaines démonstrations, présentées dans l'article sur cette question, nécessitent la définition de longueur au sens de Jordan.
Approche formelle
L'ensemble d'arrivée n'est maintenant plus nécessairement euclidien, (E, d) désigne dans ce paragraphe un espace métrique et I toujours un intervalle de R. Le couple (I, f) est un arc, c'est-à-dire une fonction continue de I dans E. La logique suivie pour la définition est proche de celle utilisée pour l'intégrale de Riemann. Soit S une suite finie a0, ..., an strictement croissante d'éléments de I. Pour une raison de commodité, une telle suite est appelée ici un découpage de l'intervalle I.
A la suite S on peut associer la longueur L(S), définie par :
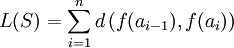

La valeur L(S) est appelée ici longueur de la ligne polygonale de sommets les images de la suite S par f. L'inégalité triangulaire impose de définir la longueur de l'arc C comme supérieure à celle d'une ligne polygonale associée à un découpage de I. La ligne droite que suit la ligne polygonale entre deux sommets consécutifs est en effet le chemin le plus rapide entre ces deux points et passer par la courbe C est nécessairement plus long. En revanche, si le découpage est très précis, on peut espérer obtenir une bonne approximation de la longueur de C, ce qui justifie la définition suivante :
-
- La longueur de l'arc C est la borne supérieure de l'ensemble des valeurs que prennent les longueurs des lignes polygonales de sommets les images d'un découpage de l'intervalle I.
Une telle définition n'impose pas à la longueur d'être finie. Par exemple une droite est de longueur infinie. Des contre-exemples moins triviaux sont donnés par la figure de droite ou encore la courbe de Peano, qui est continue mais nulle part dérivable, et dont l'image du segment [0,1] est l'ensemble des points d'un carré de côté 1. Ceci donne lieu à la définition suivante :
-
- Un arc est dit rectifiable si et seulement si sa longueur est finie.
Propriétés
-
- La longueur d'un arc géométrique est supérieure à la distance qui sépare les extrémités, si elles existent.
Cette proposition n'est que la généralisation de l'inégalité triangulaire. Dans un espace euclidien, la trajectoire la plus courte entre deux points est le segment de droite. Tout support d'arc géométrique d'extrémités ces deux points est nécessairement plus long. Cette proposition n'a d'intérêt que si les deux extrémités ne sont pas confondues, comme par exemple pour le cercle.
-
- La longueur de deux supports géométriques d'arcs qui partagent une extrémité est la somme des longueurs des deux supports.
Cette proposition est encore très intuitive. Suivre une route qui va de A à B, puis continuer jusqu'à un point C représente la même longueur que suivre la même route pour aller de A à C.
-
- Une homothétie d'un rapport k (qui suppose que l'ensemble d'arrivé dispose d'une multiplication externe, comme un espace vectoriel) appliquée un arc géométrique, accroit la longueur de l'arc d'un rapport k, si la distance est issue d'une norme.
Une dernière propriété est utile pour assurer la cohérence de la définition de longueur. Ici E désigne à nouveau un espace euclidien :
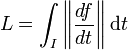
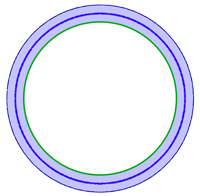
Les arcs paramétrés rectifiable sur un espace E sont dotés d'une distance naturelle, celle de la continuité uniforme. Il est naturel de s'interroger sur la continuité de la fonction qui, à un arc associe sa longueur. La figure de gauche montre que cette fonction n'est pas continue. En effet, dire qu'un arc, en rouge sur la figure, est proche d'un autre, le cercle bleu sur la figure, signifie que l'arc se trouve dans une espèce de tube, de petite largeur. La courbe en rouge montre qu'il est possible de construire une telle courbe qui oscille suffisamment pour avoir une longueur très différente. En revanche, si la courbe rouge est proche de la bleue, sa longueur ne peut être beaucoup plus petite que la bleue. Celle de plus petite longueur est illustrée à droite en vert. On parle de semi-continuité inférieure.
-
- La fonction longueur de l'ensemble des arcs paramétrés rectifiables d'un espace métrique E dans R, munis de la norme de la convergence uniforme, qui à un arc associe sa longueur, est semi-continue inférieurement.
-
- L'intégrale de la norme de la dérivée de f sur l'intervalle I est convergente et la longueur L de l'arc (I, f) au sens de Jordan est égale à celle définie par l'intégrale de la norme de sa dérivée :
Soit ε un réel strictement positif. Le fait que l'arc soit rectifiable se traduit par l'existence d'un découpage de I : a0, ... an tel que la longueur de la ligne polygonale des images par f approxime L, la longueur de l'arc à ε/3 près. Ces hypothèses se traduisent par la majoration :
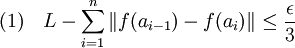
Sur le segment [a0, an], la dérivée de f est une fonction uniformément continue. On en déduit que, quitte à affiner le découpage choisi :
![\forall i \in [1,n],\;\forall x \in [a_{i-1},a_i] \quad \|\frac {df}{dx}(a_{i-1}) - \frac {df}{dx}(x)\|\ \le \frac {\epsilon}{3(a_n - a_0)}](https://static.techno-science.net/illustration/Definitions/autres/3/3f84e958f2f7655593487473e92ccd8b_68a2fd738b8d9b3929c7cf010f32c01d.png)
Ceci montre que, d'après la définition de la dérivée :
![\forall i \in [1,n-1]\quad \|f(a_i) - f(a_{i-1}) -\frac {df}{dx}(a_{i-1}) (a_i - a_{i-1})\| \le \frac {\epsilon(a_i -a_{i-1})}{3(a_n - a_0)}](https://static.techno-science.net/illustration/Definitions/autres/a/aa8219a83c56b78ca9a5f35c03b65add_dfcdea11d94867c86f4efcf39cb2d461.png)
En sommant ces n - 1 majorations, on obtient :
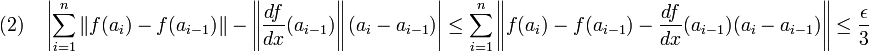
En combinant les majorations (1) et (2), on obtient :
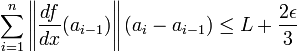
La dernière majoration est vraie pour tout découpage de I suffisamment fin. Ce qui indique que l'intégrale impropre de la norme de la dérivée de f entre a et b est convergente. Autrement dit, quitte à encore affiner le découpage, on dispose aussi de la troisième majoration :
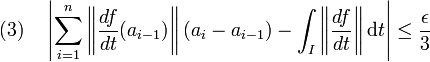
En sommant les trois majorations (1), (2) et (3), on obtient :
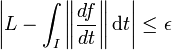
La dernière majoration étant vraie pour tout ε strictement positif, l'égalité entre la longueur de l'arc et l'intégrale est bien vérifiée.
-
- La fonction longueur est semi-continue inférieurement :
Soient (I, f) un arc paramétré rectifiable, (I, g) un autre arc paramétré, proche du premier au sens de la convergence uniforme et ε un réel strictement positif. L'objectif est de trouver un réel strictement positif μ tel que, si Lf et Lg désigne respectivement la longueur de f et de g :
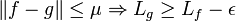
Le fait que f soit rectifiable indique l'existence d'un découpage d de f, noté (a0, ..., an), tel que polygone P associé à ce découpage et à f, ait une longueur LP proche à ε/2 de celle de f :
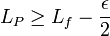
Considérons le polygone Q, de découpage d, associée à g, la longueur du polygone Q est plus petite que celle de g, par définition de la longueur d'un arc. Si la distance entre f et g est plus petite que μ, alors la distance entre P et Q au points du découpage est aussi plus petite que μ, on en déduit :
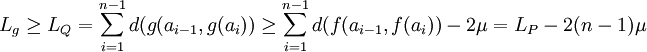
En choisissant μ plus petit que ε/4n, on obtient :
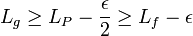
Ce qui montre la semi-continuité inférieure recherchée.