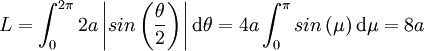Longueur d'un arc - Définition
La liste des auteurs de cet article est disponible ici.
Arc de classe C1
Une approche cinématique
Le XVIIe siècle est celui de Galilée. La notion de vitesse instantanée prend un sens, et même deux. La vitesse est tout d'abord un vecteur, celui qu'il faut multiplier par une durée a pour connaître la position d'un point se déplaçant de manière rectiligne uniforme au bout d'un délai a. C'est aussi un scalaire, celui qui indique la distance parcourue au bout de la durée a, dans le cas d'un déplacement uniforme. On parle de vitesse curviligne pour différencier cette grandeur de la vitesse vectorielle. La vitesse curviligne correspond à la norme du vecteur vitesse. Souvent, le terme de vitesse, utilisé dans le langage courant, correspond à la vitesse curviligne, par exemple dans l'expression vitesse de 80 km/h, qui correspond à un scalaire et non à un vecteur.
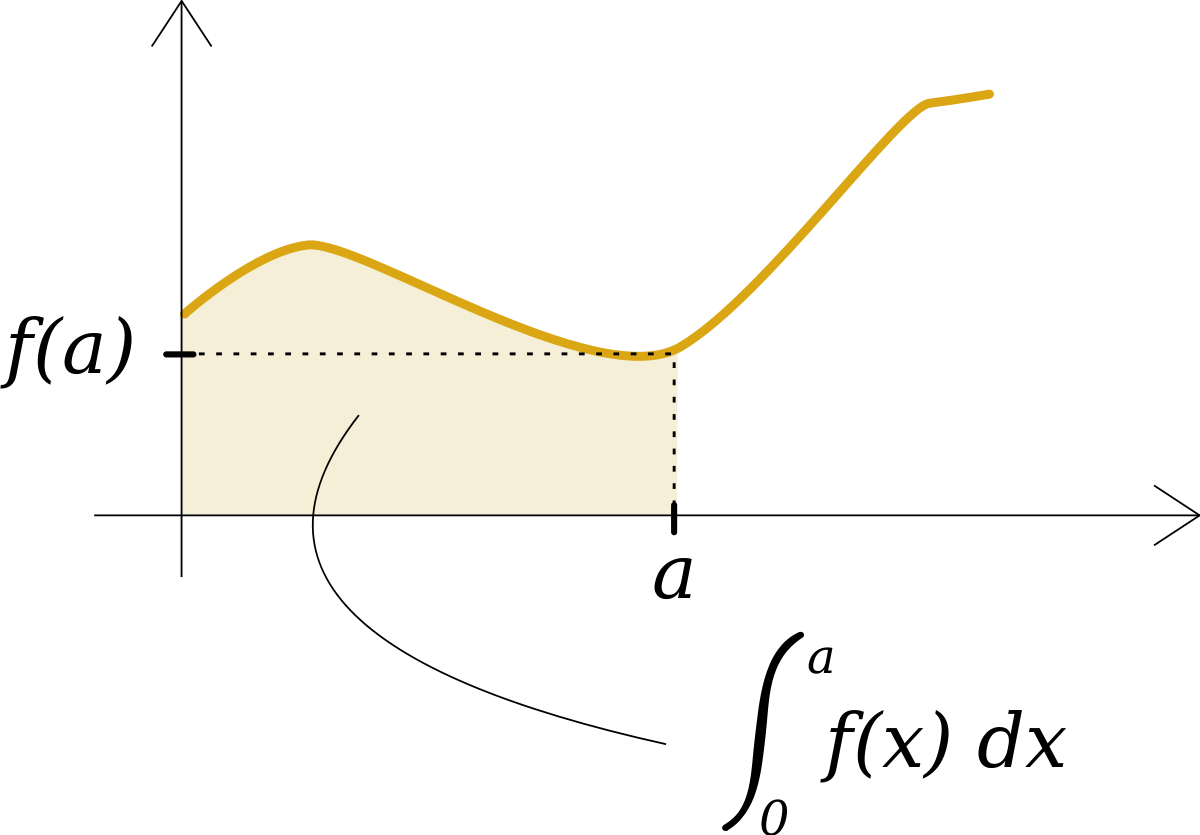
Cette définition permet une nouvelle manière d'appréhender la longueur d'un arc. Pour connaître cette longueur, il suffit de trouver une fourmi, supposée petite, se déplaçant toujours à une vitesse curviligne f constante, de lui faire parcourir l'arc. Si la durée du parcours de l'arc est égale à a, alors sa longueur est a.f. Si cette idée est fructueuse, elle demande à être aménagée. Modéliser le parcours d'un arc à vitesse constante est une question souvent plus difficile que le calcul de la longueur recherchée. Si la vitesse f est constante, la longueur peut être vue comme la surface d'un rectangle de longueur le temps a, nécessaire pour parcourir l'arc et de hauteur f. Si la vitesse n'est pas constante, on remplace la droite y = f dans un repère cartésien par la ligne d'équation y = f(t), où t varie entre 0 et a. La longueur de l'arc est égale à l'aire située entre les trois droites x = 0, x = a, y = 0 et la ligne y = f(t). On trouve l'aire illustrée en jaune sur la figure de droite.
Cette nouvelle approche prend forme à travers l'étude de la parabole semi-cubique, d'équation cy2 = x3. Vers 1660, ce problème est célèbre et intéresse de nombreux mathématiciens. La question du calcul de la longueur d'un arc, que l'on appelait alors problème de rectification était à l'époque considéré comme très difficile, voir souvent impossible. John Wallis publie la solution en 1659 et en attribue la paternité à Neil. Une des raisons de la célébrité de la preuve est qu'elle débouche sur une valeur constructible à la règle et au compas, naissance d'un fol espoir de résolution de la quadrature du cercle. Cette solution est reproduite par Van Heuraet la même année avec une méthode de rectification de la parabole à l'aide du calcul de la quadrature d'une hyperbole. Le problème de la quadrature d'une surface est celui consistant à déterminer son aire. En 1660 Pierre de Fermat généralise l'approche à toute courbe, qu'à l'époque on imagine comme toujours dérivable, au moins par morceau, même si la notion de dérivée n'est pas encore formalisée.
Le pas de géant est franchi entre 20 et 30 ans plus tard, Isaac Newton et Gottfried Leibniz découvrent le calcul infinitésimal et le théorème fondamental de l'analyse, indiquant la relation entre la dérivée et l'intégrale. La longueur L d'un arc parcouru durant une période de a à une vitesse curviligne égale à f(t) à l'instant t est égale à :
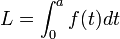
Définitions
Pour être précis, quelques définitions doivent être données. Ici, E désigne un espace euclidien de dimension n et R l'ensemble des nombres réels. Pour définir une longueur, il est utile d'associer un sens précis au mot arc paramétré de classe Cp, si p est un entier positif:
Définition d'un arc paramétré — Un arc paramétré de classe Cp est un couple (I, f) composée d'un intervalle I de R et d'une fonction de I dans un espace euclidien, p fois dérivable, dont la dérivée pième est continue et dont la dérivée première ne s'annule jamais.
Demander à la dérivée première de ne jamais s'annuler permet d'éviter des singularités qui ne sont pas l'objet de cet article. Cette définition fournit à la fois l'arc et une manière de le parcourir. Pourtant, géométriquement, parcourir un arc rapidement ou lentement, dans un sens ou dans un autre, ne modifie pas la nature de l'arc. Pour cette raison, on définit une classe d'équivalence entre les arcs paramétrés :
Définition d'arcs Cp italiques — Soient (I, f) (J, g) deux arcs paramétrés à valeurs dans E. S'il existe un difféomorphisme θ de classe Cp de I dans J tel que goθ soit égal à f on dit que les deux arcs paramétrés sont Cp italiques.
On parle aussi d'arcs équivalents au lieu d'arc Cp italiques. Avec cette définition, le parcours deux fois d'un cercle par un arc paramétré n'est jamais équivalent à un arc paramétré parcourant une seule fois le cercle. En effet, dans un cas tout point du cercle possède deux antécédents et dans l'autre cas un unique, un difféomorphisme ne peut exister. On peut maintenant énoncer la définition d'un arc géométrique :
Définition d'un arc géométrique de classe Cp — Un arc géométrique est une classe d'équivalence d'arcs Cp italiques.
Il devient possible de définir rigoureusement la longueur d'un arc géométrique :
Définition de la longueur d'un arc géométrique de classe Cp — La longueur d'un arc géométrique ayant pour représentant (I, f) est la valeur L de l'intégrale suivante, égale à un nombre positif ou à l'infini :
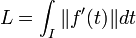
L'intégrale n'est pas nécessairement finie car l'intervalle I n'est pas nécessairement un segment. Par exemple, si I est égal à R et f à la fonction qui à t associe exp(i.t) à valeurs dans les nombres complexes identifiés au plan euclidien, l'arc géométrique parcourt un nombre infini de fois le cercle unité, sa longueur est infinie.
Pour que la définition fasse sens, il est nécessaire que les longueurs de deux arcs Cp italiques soient les mêmes. On le vérifie simplement. Si (I, f) et (J, g) sont deux arcs paramétrés Cp italiques et si le difféomorphisme θ vérifie goθ = f, alors l'intégration par changement de variable montre que :
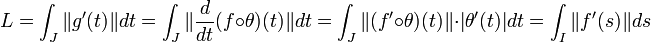
Formulation
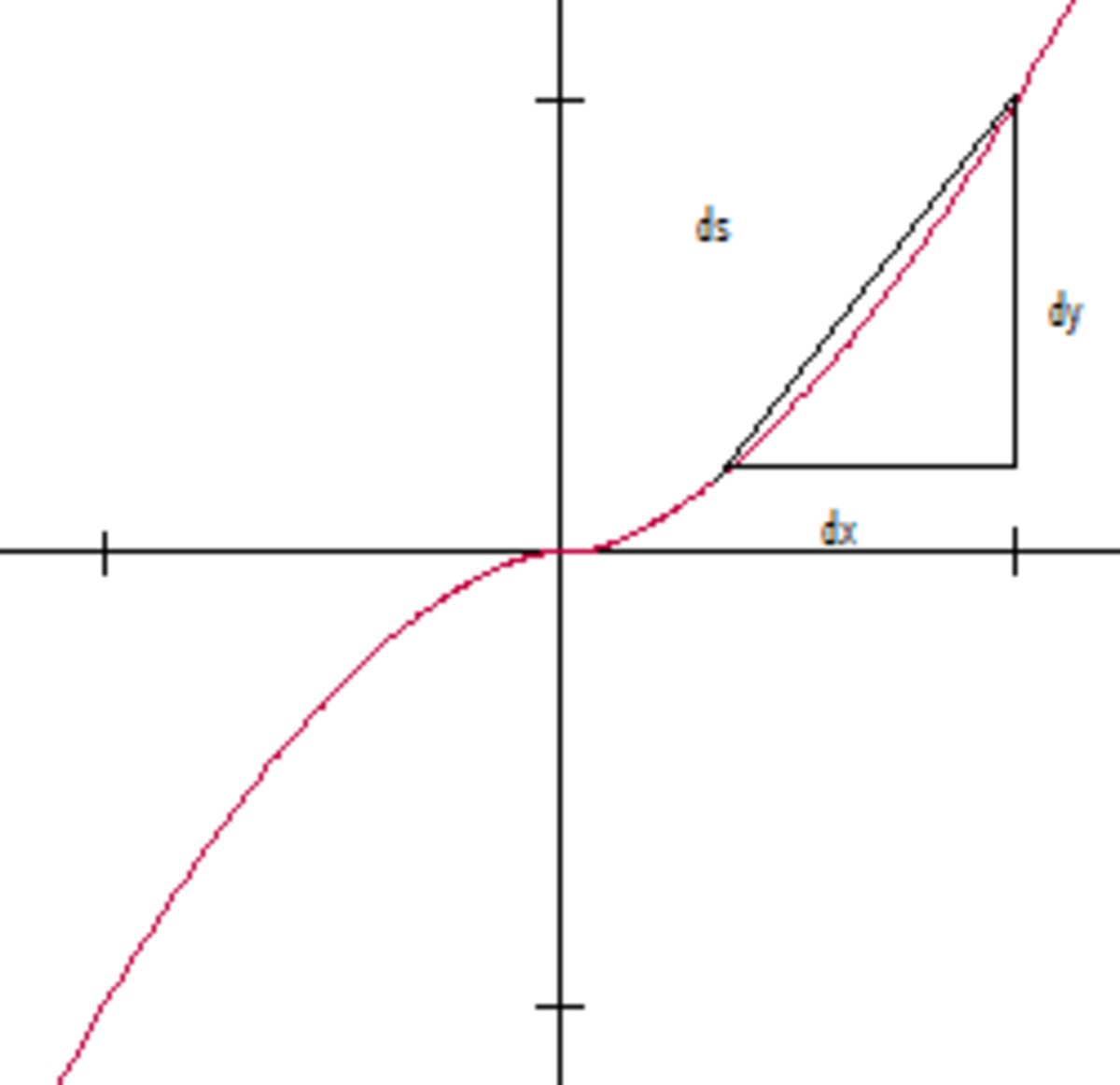
Si E désigne un plan euclidien, la fonction f peut s'exprimer à l'aide de deux fonctions coordonnées, de I dans R, notées ici x(t) et y(t). Si les coordonnées s'expriment dans une base orthonormale et si ]a, b[ désigne l'intervalle I, la formule précédente devient :
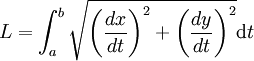
Sous cette forme, la longueur de l'arc trouve une autre justification intuitive que celle de la vitesse. Soit t et dt deux réels positifs tel que t et t + dt soient éléments de I. Notons (x, y) les coordonnées de l'image de t et (x+dx, y+dy) celle de t + dt. Cette situation est illustrée sur la figure de droite. Si dt est suffisamment petit, la courbe est proche de son approximation tangente. Identifier entre ces deux valeurs du paramètre l'arc avec son approximation linéaire tangente au point t ramène le localement le calcul à celui de la longueur ds de l'hypoténuse d'un triangle rectangle, qui se calcule avec le théorème de pythagore :
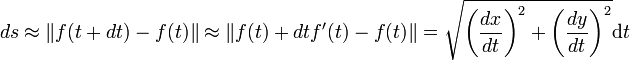
Il existe un cas particulier usuel, celui où la courbe est représentée par le graphe de l'équation y = f(x). Ici f désigne une fonction de classe C1 d'un intervalle I à valeur dans R. Pour revenir à une situation plus proche de la précédente, on peut considérer que la courbe est représentée par l'arc paramétré (I, F) où F est la fonction de I dans R2 qui à t associe (t, f(t)). En supposant toujours que ]a, b[ désigne l'intervalle I, on obtient :
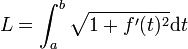
Il est parfois plus habile d'utiliser les coordonnées polaires pour exprimer l'arc paramétré, ce qui revient à utiliser les notations suivantes :
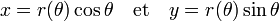
On en déduit :
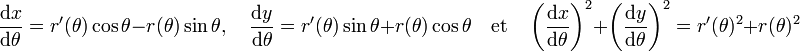
Ce qui permet d'établir la formule :
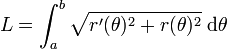
En dimension 3 et sous les mêmes hypothèses, la formule prend la forme :
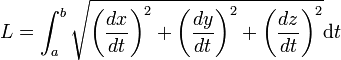
Exemples
Au XVIIe siècle, le problème de la rectification d'un arc est à la pointe de la recherche. Sans les outils du calcul différentiel, ces questions demandent une grande imagination pour y répondre. Elles deviennent beaucoup plus aisées une fois connue la dérivée et sa relation avec l'intégrale. Un exemple est celui de la chaînette, courbe plane qui correspond à la forme que prend un câble lorsqu'il est suspendu par ses extrémités et soumis à son propre poids. Il est résolu en 1691 à la fois par Leibniz, Huygens et les frères Bernoulli. Si ch désigne le cosinus hyperbolique et si a désigne un réel strictement positif, son équation est la suivante :
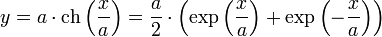
La longueur L0 de la chaînette entre le point d'abscisse 0 et celui d'abscisse x0 est donnée par la formule, si sh désigne le sinus hyperbolique :
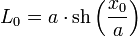
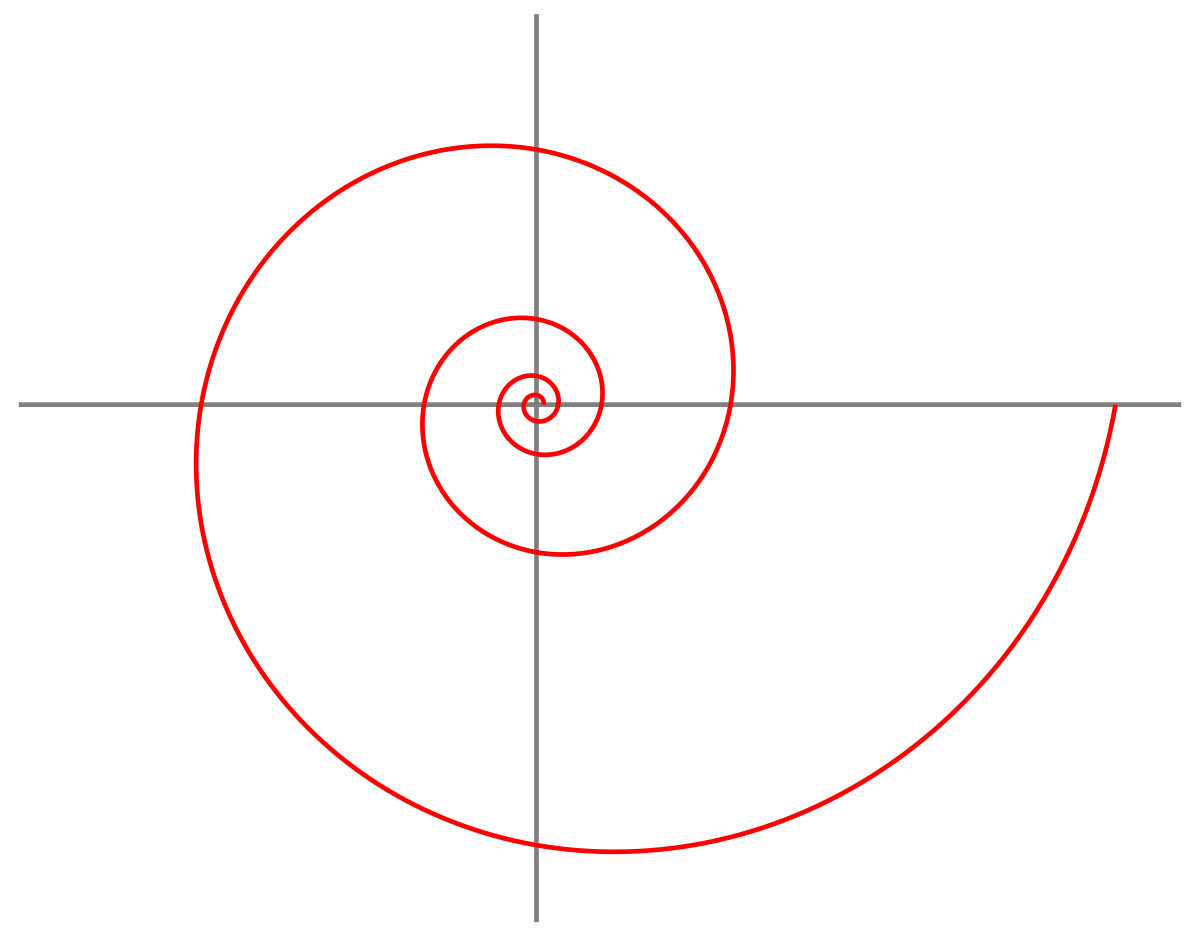
Le calcul de la longueur d'une spirale logarithmique est d'abord déterminé sans l'usage du calcul différentiel. Son usage permet une résolution du problème de manière très simple, surtout si le paramétrage proposé est polaire si a est un réel strictement positif et b est strictement supérieur à 1 :
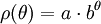
La longueur Lθ de la spirale entre le point origine et celui d'angle θ, qui peut être supérieur à 2.π, est donnée par la formule suivante :
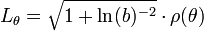
Un autre calcul est d'importance historique, celui de la parabole de Neil, qui correspond à la courbe d'équation y = ±a.x3/2, si a est un entier strictement positif. Sa rectification est réalisée avant la découverte du calcul différentiel. La nouveauté apportée réside dans le fait que, si L0 désigne la longueur de la partie positive de la branche située entre 0 et x0, le résultat intermédiaire suivant est utilisé :
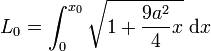
Une question de rectification est finalement liée à un problème de quadrature, c'est-à-dire au calcul d'une surface, base de la définition utilisée dans ce paragraphe. Au final, on trouve :
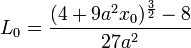
Cette démarche permet de résoudre le problème de la rectification de la parabole. Si l'on choisit le paramétrage suivant y = a.x2, avec a un réel strictement positif, la longueur L0 de la branche située entre 0 et x0 s'exprime sous la forme d'une quadrature d'hyperbole, que l'on sait réaliser déjà depuis plus de 20 ans :
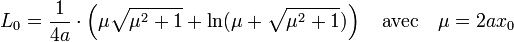
Si l'approche par la vitesse permet de résoudre aisément la question de la longueur de l'arche d'une cycloïde, égale à 8 fois le rayon du cercle, un problème en apparence aussi simple que de calculer la circonférence de l'ellipse en fonction des demi-axes conduit à des intégrales qu'on ne peut pas expliciter plus avant : on parle d'intégrales elliptiques de seconde espèce.
Les calculs sont analogues en dimension 3. L'article Loxodromie explicite un exemple.
-
- Rectification de la chaînette :
On utilise ici la paramétrisation par une fonction f, définie par f(x) = a.ch(x/a). On obtient les expressions :
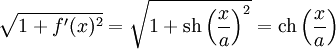
On en déduit :
![L_0 = \int_0^{x_0} \operatorname{ch}\left(\frac xa\right)\mathrm d x = \left[ a\cdot \operatorname{sh}\left(\frac xa\right)\right]_0^{x_0} = a\cdot \operatorname{sh}\left(\frac {x_0}a\right)](https://static.techno-science.net/illustration/Definitions/autres/e/e966d345b93f5d9e2e9d1e76d5dbf9f5_b3b3079c5398a4392f7e5a77ff403821.png)
-
- Rectification de la spirale logarithmique :
A l'aide des coordonnées polaires, on obtient :
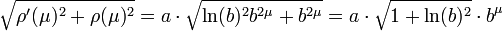
On en déduit :
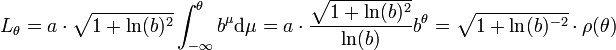
-
- Rectification de la parabole de Neil :
L'arc est paramétré par la courbe y = f(x), ce qui amène le calcul :
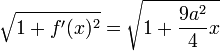
Puis, en utilisant le changement de variable u = 9a2/4.x :
![L_0 = \int_0^{x_0}\sqrt{1 + \frac {9a^2}4 x} \;\mathrm d x = \frac 4{9a^2}\int_0^{\frac {9a^2}4x_0}\sqrt{1 + u}\;\mathrm d u = \frac 8{27a^2} \left[ (1 + u)^{\frac 32}\right]_0^{\frac {9a^2}4x_0} =\frac {(4 + 9a^2x_0)^{\frac 32} - 8}{27a^2}](https://static.techno-science.net/illustration/Definitions/autres/9/94ae0d3303891e35579e13d569b4a983_fc399deaafd6f6a5819322748e71a4af.png)
-
- Rectification de la parabole :
La rectification de la parabole est un peu plus subtile. Avec les notations précédentes :
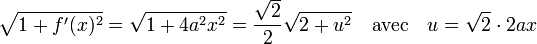
On en déduit :
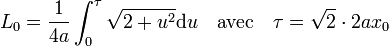
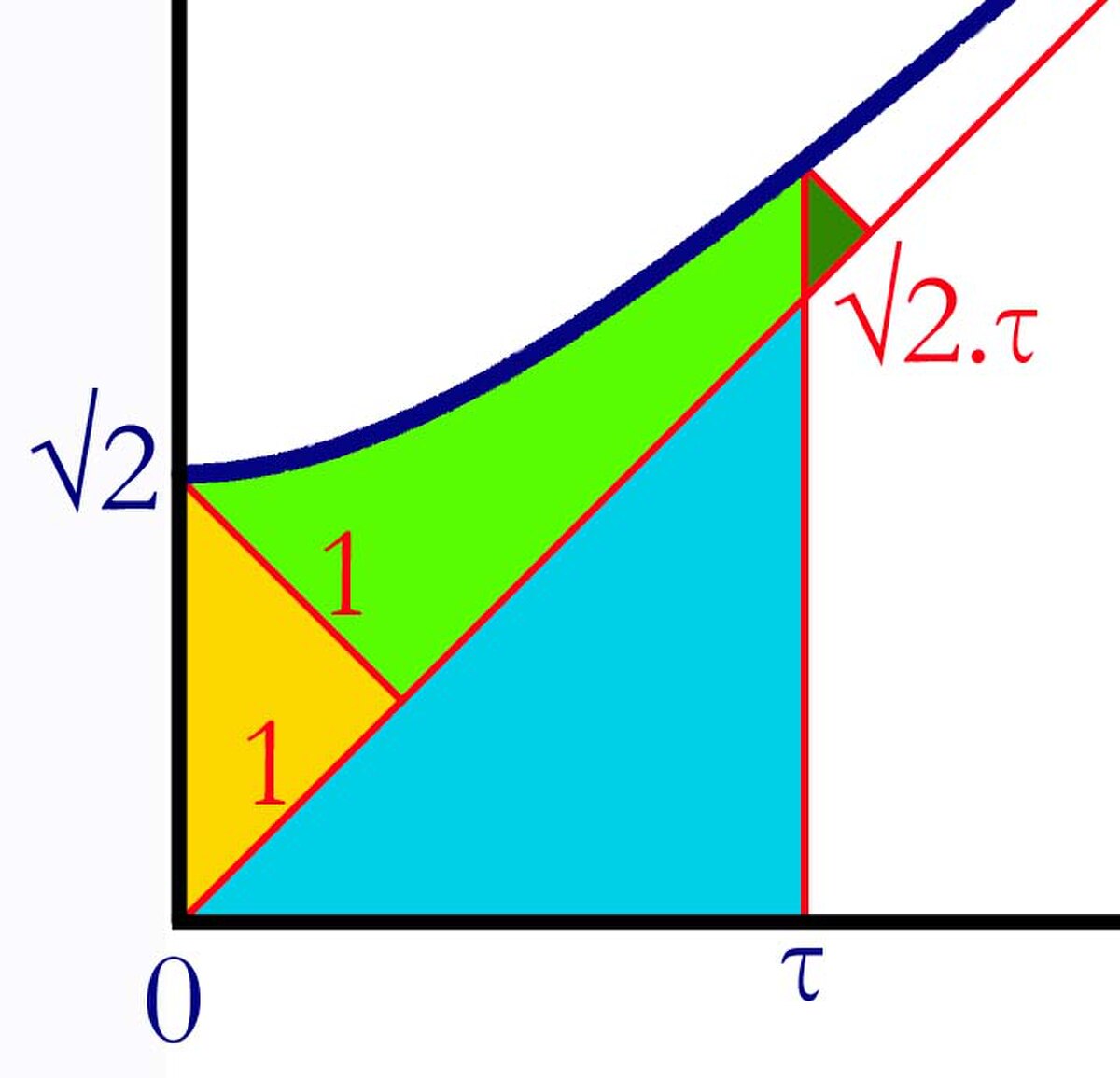
L'aire à déterminer est illustrée sur la figure de droite. Elle est comprise entre les deux droites d'équations x = 0 et x = τ, puis entre la droite y = 0 et la fonction dont l'équation est sous l'intégrale. Sans disposer des outils puissants de l'analyse, il est possible de calculer cet aire. On la découpe en trois zones, la jaune, la bleue et la vert claire.
La zone jaune correspond à un demi carré de côté 1, la bleue à un demi carré de côté τ. Déterminons la surface vf du triangle vert foncé. Pour cela, il suffit de calculer la longueur de sa diagonale vd :
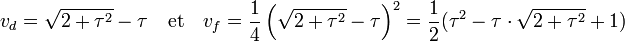
Il reste encore à déterminer l'aire de la zone vert claire vc, elle est égale à la différence entre l'aire de zone verte v et de la zone vert foncé. La zone verte correspond au logarithme de la distance qui sépare l'origine du sommet du triangle vert foncé le plus éloigné, on trouve :
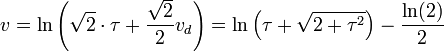
On en déduit :
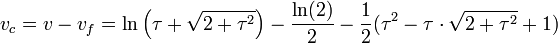
Ce qui montre que, si √2μ = τ:
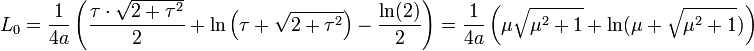
-
- Rectification de la cycloïde :
Un paramétrage usuelle de la cycloïde de rayon a est le suivant :
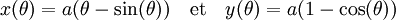
Ce paramétrage permet le calcul de la norme de la dérivée :
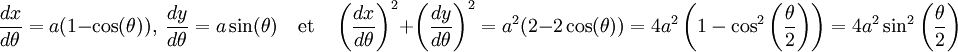
Si L désigne la longueur recherchée :