Longueur d'un arc - Définition
La liste des auteurs de cet article est disponible ici.
Contenu de Minkowski
Motivation
Minkowski s'intéresse surtout aux courbes fermés et simples car elles définissent une frontière d'un espace compact dans le plan euclidien. Les résultats qu'il établit sont particulièrement intéressants s'il peut les généraliser aux dimensions supérieures.
Les outils issus de la géométrie différentielle ne sont pas toujours très adaptés pour cela. Un exemple est donné par le théorème isopérimétrique, dans le cas général on cherche à démontrer un solide d'un espace euclidien de dimension n possède un volume plus petit que celui de la boule de même surface. Le terme de boule de rayon r désigne l'ensemble des points à une distance inférieure à r d'un point donné appelé centre. Il n'est pas trop complexe de montrer que la courbure moyenne en chaque point d'une surface, frontière d'un solide qui atteint l'optimum isopérimétrique, est nécessairement constante. En dimension 2, il est très simple de montrer que l'unique courbe simple et fermé de courbure moyenne constante est le cercle, une démonstration naturelle est l'œuvre d'Hurwitz et utilise l'inégalité de Wirtinger. En dimension 3, la démonstration est connue, mais elle est suffisamment technique pour ne dater que du début du XXe siècle. Le cas général n'est toujours pas démontré.
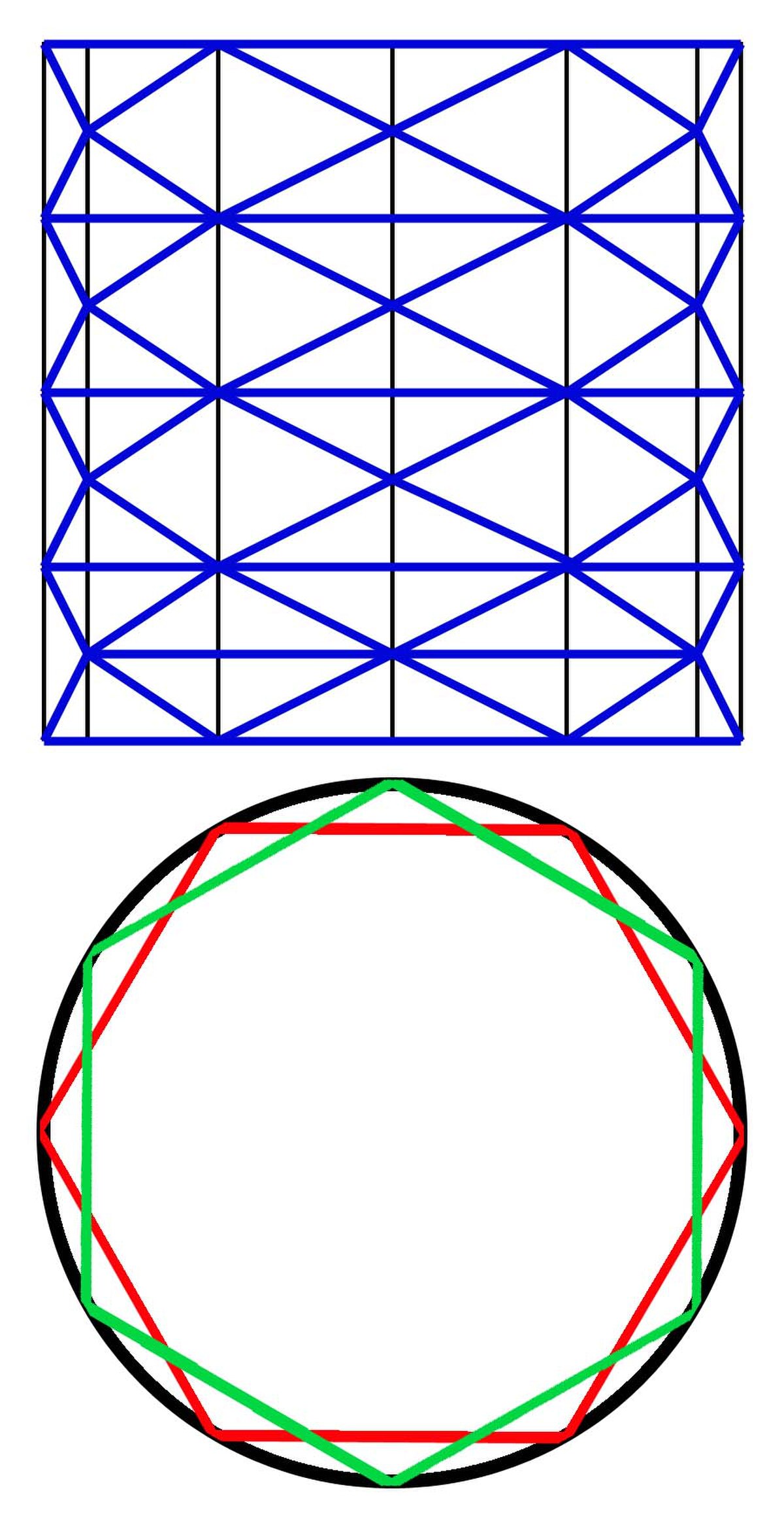
La définition de Jordan pour la longueur d'une courbe n'est pas adaptée non plus car elle ne se généralise pas directement aux dimensions supérieures. La généralisation naturelle consisterait à définir l'aire de la surface d'une portion de cylindre comme la borne supérieure de la surface d'un polyèdre dont les sommets se trouveraient sur la frontière du cylindre. L'exemple sur la droite illustre l'inconsistance d'une telle généralisation. le polyèdre utilisé est un lampion dont les sommets sont situés sur des hexagones parallèles, chaque fois décalés d'un douzième de tour. Si les plans des hexagones se rapprochent de plus en plus, la surface du polyèdre augmente jusqu'à l'infini.
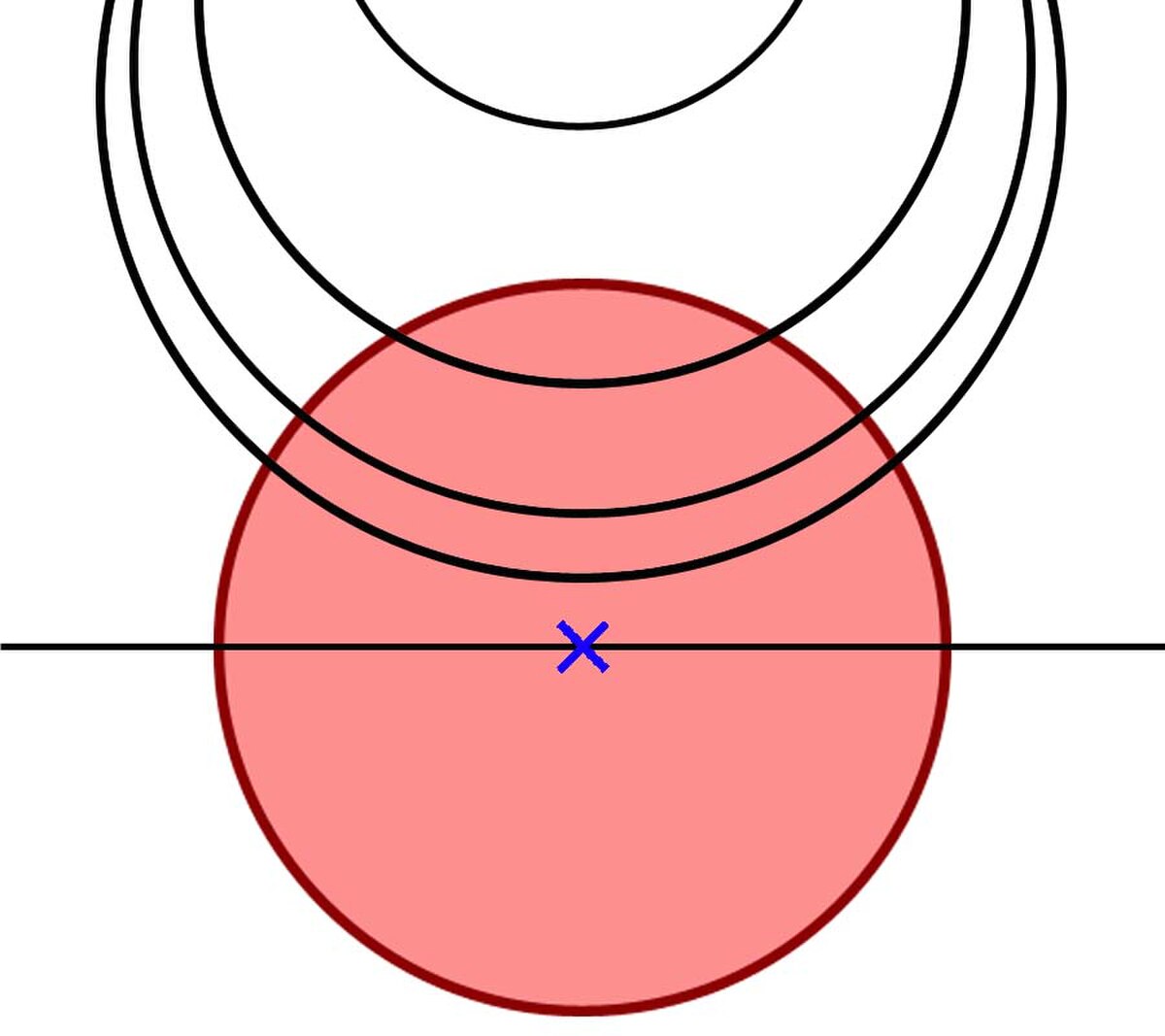
Minkowski trouve une solution pour définir la longueur d'un arc qui résiste au passage à une dimension supérieure. Son approche intuitive est différente de celles considérées jusqu'ici. Il ne s'appuie pas comme Jordan sur la longueur d'une ligne polygonale, mais directement sur la fonction volume de l'espace euclidien de dimension n. Cette fonction est en général définie par la mesure de Lebesgue. Pour une valeur ε, suffisamment petite, Il considère les points à une distance inférieure à ε de la courbe C qu'il étudie. Il obtient un ensemble, illustré en rose sur un exemple en dimension 2 sur la figure de gauche, la courbe C est représentée en bleu. Un tel ensemble est appelé un tube.
Si la valeur ε diminue, le volume du tube se rapproche du produit de la longueur de l'arc par le volume de la boule de dimension n - 1 et de rayon ε. Dans le cas du cercle de rayon r et en dimension 2, le tube est constitué de la zone de l'espace compris entre un cercle de rayon r + ε et un autre de même centre et de rayon r - ε. Son volume est exactement 2π.r que multiplie 2ε. En dimension 3, le tube est un tore, une fois encore son volume est exactement le produit de 2π.r par la surface d'un disque de rayon ε. Cette définition, si elle est un peu plus complexe à mettre en œuvre, se généralise aisément aux dimensions supérieures.
Si ε est un entier plus petit que r, la zone Cε est celle qui se trouve à l'intérieur d'un disque de rayon r + ε et à l'extérieur du disque ouvert de rayon r - ε. La surface Vol (Cε) est égale à :
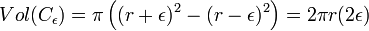
Or, 2π.r correspond à la longueur du cercle et en dimension 1, la boule de rayon ε est de volume égal à 2.ε en dimension 1. Le contenu de Minkowski est bien égal à la longueur du cercle.
Formalisme
Minkowski, avec Hausdorff, développent des outils permettant de mieux appréhender l'étude général des solides. L'ensemble étudié est celui des compacts non vides d'un espace euclidien E, de dimension n. La somme de Minkowski associent à deux ensembles A et B le solide A + B composé des sommes d'éléments de A et de B. Cet ensemble est équipé d'une distance, dite de distance de Hausdorff. Le tube étudié correspond à la somme d'un compact C, correspondant à la courbe dont on souhaite mesurer la longueur et de la boule de rayon ε, il est noté ici Cε.
Si la courbe C est simple et fermée et de classe C2, alors le volume du tube Vol(Cε) s'exprime en fonction de la longueur LC de l'arc C et du volume Vol(Bn-1(ε)) de la boule d'un espace euclidien de dimension n - 1 et de rayon ε, ceci à condition que ε reste suffisamment petit :
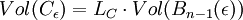
Si la courbe n'est pas fermée, l'égalité reste vraie si l'on ajoute le volume d'une boule de rayon ε en dimension n. En effet, deux demi boules vont s'ajouter, chacune à l'une des extrémités de la courbe, on obtient :
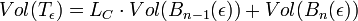
Quelle que soit la configuration précédente, on obtient une nouvelle manière de définir la longueur d'un arc :
-
- Le contenu 1 dimensionnel d'un ensemble C d'un espace euclidien de dimension n, noté M1(C), est la limite suivante, quand elle existe :
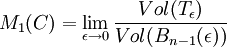
Cette définition est bien une généralisation de la longueur définie précédemment :
-
- Si C est l'ensemble d'arrivé d'un arc paramétré compact de classe C2, la longueur de C est égale à son contenu 1 dimensionnel.
Cette définition est particulièrement pertinente dans le cas de l'étude de la longueur de la frontière d'une surface S compacte en dimension 2 de frontière C. Si la frontière est paramétrable par un arc de classe C2, on dispose du théorème suivant, appelé formule de Steiner-Minkowski :
-
- La longueur LC de l'arc C est égale à la limite suivante :
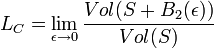
Le contenu de Minkowski permet de généraliser à de nombreuses surfaces cette formule.
Fixons les notations, E est un espace euclidien de dimension n, ([a, b], f) est un paramétrage curviligne de classe C2 d'un arc géométrique, fermé et simple et dont l'image est égale à C. Dire que le paramétrage est fermé revient à dire que f(a) est égal à f(b), dire qu'il est simple est équivalent à dire que si s et t sont deux éléments de ]a, b[, alors f(s) est différent de f(t). Enfin, dire que le paramétrage est curviligne revient à dire que la norme de la dérivée de f(t) est toujours égale à 1, si t est un élément de [a, b]. La valeur ε désigne un réel strictement positif, compris entre 0 et μ, où μ est un réel strictement positif à déterminer. Ht désigne l'hyperplan de E orthogonal à f(t) et Ba,μ la boule unité fermée de l'hyperplan Ha et de rayon μ. On note ut la dérivée de f au point t et vt le vecteur de norme 1 colinéaire à la dérivée seconde de f et de même sens. Dire que f est un paramétrage curviligne implique que ut et vt sont orthogonaux. Enfin, on note c(t) la courbure de f en t, la dérivée seconde de f en t est égale au produit de c(t) par vt.
La technique utilisée pour la démonstration consiste à construire un plongement ψ de [a, b]xBa,μ dans Cμ de classe C1. Ce plongement fournit le bon changement de variable pour calculer l'intégrale donnant l'aire de Cε. Pour construire ψ, on construit une application φt de classe C1 de [a, b] à valeurs dans les rotations de E, tel que tel que l'image de ua par φt soit égal à ut.
-
-
- Construction de φt :
-
- Equation différentielle :
- Une solution élégante consiste à construire φt comme la solution d'une équation différentielle linéaire. Pour cela, on définit une application χ d'un ensemble D dans L(E) l'ensemble des endomorphismes de l'espace E. Ici D désigne les couples (u, v) de vecteurs de E tel que u et v soient de normes égales à 1 et tel que u et v soient orthogonaux. L'endomorphisme χ(u,v) associe à u le vecteur v, à v le vecteur -u et le vecteur nul à tout vecteur orthogonal à u et à v. On remarque que pour tout vecteur z de E, le produit scalaire de z avec son image par χ(u,v) est nul. En effet, il est possible d'écrire z sous la forme α.u + β.v + w, où α et β sont deux scalaires et w un vecteur orthogonal à u et à v. On a bien, si <.,.> désigne le produit scalaire :
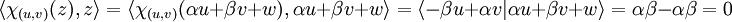
- Cette application nous permet de définir la fonction ψ, de [a, b] dans L(E), par :
![\forall t \in [a, b]\quad \psi_t = c (t) \chi_{(u_t,v_t)}](https://static.techno-science.net/illustration/Definitions/autres/8/86e12e5cc3c69589b4736fd75007e103_a99895d0c3e657ec0b4e24213195f818.png)
- L'application ψ est bien continue, elle est en effet composée d'applications continues. Il existe une petite difficulté si la courbure c(t) est nulle, car vt n'est pas défini, mais définir ψ comme nulle en ces points est clairement un prolongement par continuité, la norme de ψt étant égale à c(t). La norme choisie ici pour L(E) est celle qui, à un endomorphisme associe la borne supérieure de la norme de l'image de la boule unité. On considère l'équation différentielle suivante, sur [a, b] et à valeurs dans L(E):
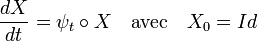
- La continuité de ψ et la compacité de [a, b] montrent que la fonction, qui à t associe la norme de ψ, atteint sa borne supérieure m. L'application qui à X associe la composée de ψ et de X est donc continue et m-lipschitzienne. Le théorème de Cauchy-Lipschitz garantit l'existence d'une solution unique φ à l'équation différentielle. Il est même possible de donner une expression explicite de φ :
![\forall t \in [a, b]\quad \varphi_t = \exp \left(\int_a^t \psi_{\tau} d\tau \right)\quad\text{avec, si}\quad m \in \mathcal L(E) \quad \exp(m)=\sum_{n=0}^{\infty} \frac {m^n}{n!}](https://static.techno-science.net/illustration/Definitions/autres/d/d9a86fb42da1dc2e566e813f7d1d74ca_60523d62ca3de710907a3d424a4efc5a.png)
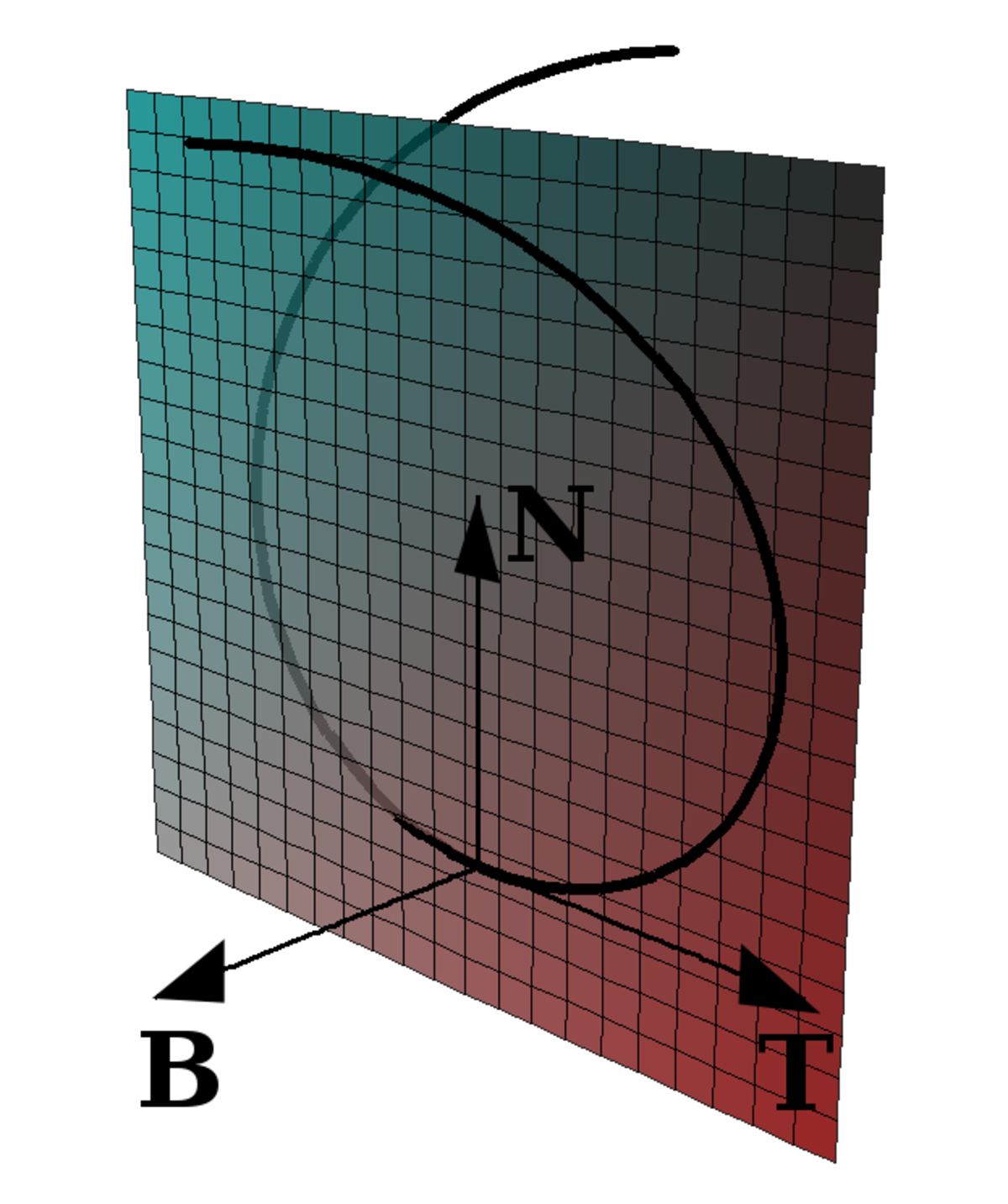
A l'exception du caractère un peu inhabituel des ensembles utilisés ici, la méthode proposée n'utilise qu'une équation différentielle linéaire très simple. L'application φ permet presque de définir un repère de Frenet. Il suffirait d'associer au point a une base de Frenet et la base de Frenet serait, au point t son image par φ. Ce résultat n'est vrai que si la courbe est birégulière, c'est-à-dire que la dérivée seconde de f s'annule jamais. Après le premier point d'inflexion, il n'existe aucune raison de penser que l'image de v0 soit encore colinéaire à la dérivée seconde de f. Il suffit maintenant de vérifier que φ est bien l'application recherchée.
-
- L'application φ est à valeurs dans un ensemble de rotations et l'image de ua par φt est égale à ut :
- Montrons tout d'abord que φ est à valeurs dans un ensemble de rotations. ce qui revient à montrer que si z est un vecteur de E, φt(z) est de même norme que z. Ce résultat est trivialement vrai si t est égal à a car φa est l'identité. Il suffit de montrer que la dérivée de la fonction, qui à t associe le carré de la norme de φt(z), est nulle, pour établir que φt est une isométrie :
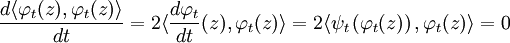
- Il reste à montrer que le déterminant de φt est égal à 1. Comme φt est une isométrie, son déterminant est égal à ±1. L'image de l'application qui à t associe det φt est un connexe car l'application est continue. Comme en a, l'application vaut 1, elle vaut 1 partout et le déterminant de φt est bien égal à 1.
- Montrons ensuite que φt(ua) est bien égal à ut. Pour cela, il suffit de vérifier que les deux arcs, qui à t associe φt(ua) d'une part et ut d'autre part ont même valeur initiale et satisfont à la même équation différentielle linéaire. L'unicité de la solution, garantie par le théorème de Cauchy-Lipschitz montre l'égalité. Par construction φa est égal à l'identité, les deux arcs ont donc bien même valeur initiale, vérifions maintenant que les deux arcs sont solutions de la même équation différentielle :
![\forall t \in [a, b]\quad \frac {d\varphi_t(u_0)}{dt} = \frac {d\varphi_t}{dt}(u_0) = \psi_t \circ \varphi_t(u_0) \quad\text{donc}\quad \frac {d\varphi_t(u_0)}{dt} =\psi_t \left( \varphi_t(u_0)\right)](https://static.techno-science.net/illustration/Definitions/autres/1/12bf7f6d550a1bc93ef9bbc01485c7a3_3f54eaedd63e0ec9d63eb0b14c4838a4.png)
- D'autre part :
![\forall t \in [a, b]\quad \frac {du_t}{dt} = c(t)v_t = c(t) \chi_{(u_t,v_t)} = \psi_t(u_t)\quad\text{donc}\quad \frac {du_t}{dt} =\psi_t(u_t)](https://static.techno-science.net/illustration/Definitions/autres/f/f5ac1e58709f68709e07af6b9ed6a258_62d976e236636272540c77eaefbd0e8f.png)
On en déduit que φt(Ha) est bien égal à Ht. En effet, Ha est l'orthogonal de ua, son image par φt est l'orthogonal de φt(ua) car φt est une rotation. Il suffit de remarquer que φt(ua) est égal à ut pour conclure.
-
- Injectivité de Γ :
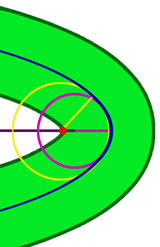
Pour que l'application Γ soit un plongement, il est nécessaire de bien choisir la valeur μ. Si elle est trop élevée, l'application Γ n'est pas nécessairement injective. Un exemple est donné sur la figure de droite. Le plus petit rayon de courbure est donnée par le point de cercle osculateur violet. La valeur μ est choisie plus grande que le rayon du cercle osculateur, appelé rayon de courbure. Le point rouge est élément de l'hyperplan orthogonal à la tangente du point de cercle osculateur violet, et il est à une distance égale à cette valeur de μ. Les points à une distance inférieure ou égale à μ de la courbe sont illustrés en vert. Le point rouge est aussi élément du plan orthogonal d'un autre point, illustré en jaune. Si μ est choisi plus petit que le plus petit rayon de courbure atteint par les points de la courbe, cette situation ne peut pas se produire. L'application Γ est alors localement injective.
-
- Injectivité locale de Γ :
- La fonction c(t) qui à t associe la courbure de l'arc au point f(t) est continue. Elle est définie sur un compact, elle atteint sa borne supérieure. Notons rm l'inverse de cette borne, qui correspond au plus petit rayon de courbure de l'arc. On suppose que μ est choisi plus petit que rm/2. l'objectif est de montrer que Γ est localement injective, c'est-à-dire que si t est un élément de [a, b], Γ est injective sur l'ensemble ]t-δ, t+δ[xBa,μ. La valeur δ correspond à un nombre réel strictement positif indépendant de t et à déterminer.
- Pour simplifier les notations, on suppose, quitte à translater l'intervalle [a, b], que t est égal à 0. On suppose de plus, quitte à modifier le repère, que f(0) est égal au vecteur nul. On va montrer qu'un point p image par Γ d'un point (0, p) de ]t-δ, t+δ[xBa,μ n'a pas d'autre antécédent dans cet ensemble. Dire que p est une telle image, revient à dire que sa norme est plus petite que μ, donc que rm/2 et que p est orthogonal à u0. On considère un autre antécédent de première coordonnée notée t et l'on va montrer que t est nécessairement plus grand qu'une valeur δ. Dire que t est un autre antécédent implique que p est dans le plan orthogonal à ut et passant par f(t). Ce qui montre l'égalité :
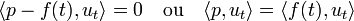
- La formule de Taylor-Lagrange montre l'existence d'une valeur τ1 comprise entre 0 et t, tel que :
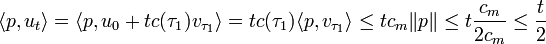
- Le même raisonnement montre l'existence de deux valeurs τ2 et τ3, aussi comprises entre 0 et t, tel que :
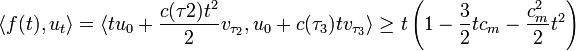
Si l'on choisit δ plus petit que min(1, 1/cm)/6, on est assuré que le terme <p, ut> est strictement plus petit que le deuxième produit scalaire, et l'injectivité locale, sur l'intervalle ]t-δ, t+δ[xBa,μ est bien garantie.
-
- Injectivité globale de Γ :
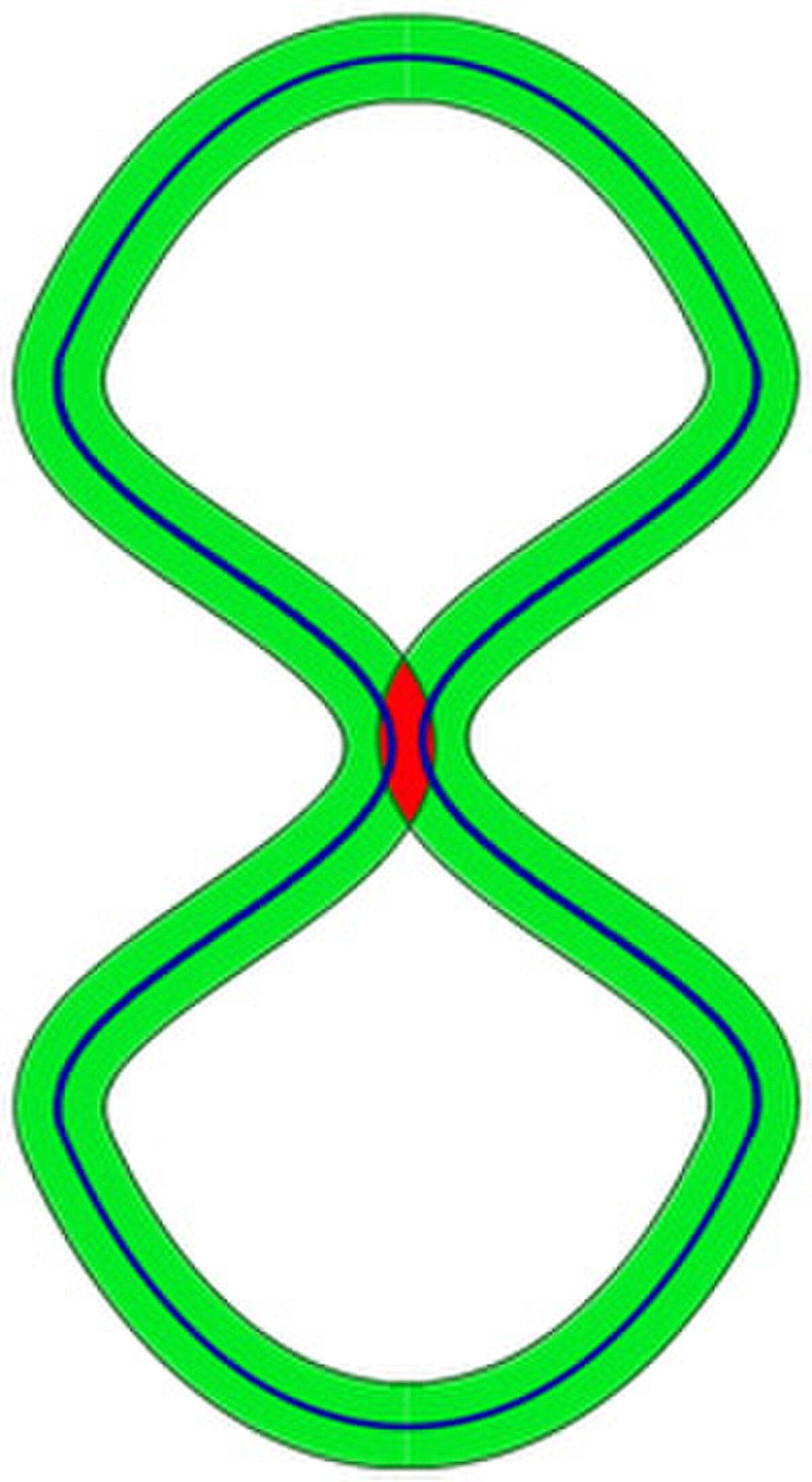
L'injectivité locale n'implique pas l'injectivité de Γ. L'illustration de droite montre la raison. Si la courbe est suffisamment pincée, un point d'abscisse éloignée peut être arbitrairement proche du point étudié. Il faut alors vérifier qu'une zone rouge, à l'image de la figure, n'existe pas si μ est bien choisi. Comme par hypothèse, l'arc ne contient pas de point double, la configuration désagréable serait celle de gauche, avec une infinité de brins de l'arc qui s'approchent de plus en plus du point critique. La compacité du segment [a, b], impliquant celle du graphe C empêche l'apparition de ce phénomène.
- Pour s'en persuader, considérons la fonction qui à t associe le minimum de la distance entre f(t) et l'image par f des intervalles [a, t - δ] et [t + δ, b]. Comme la fonction distance est continue et que l'union des segments [a, t - δ] et [t + δ, b] est un compact, ce minimum est atteint. Comme l'arc est simple, c'est-à-dire qu'il n'admet pas de point multiple, ce minimum est différent de 0. La fonction de [a, b] dans R qui à t associe le minimum défini précédemment est encore continue. Elle est encore définie sur un compact, ce qui implique qu'elle atteint encore son minimum μ1 qui n'est pas nul.
- Si la valeur μ est choisie plus strictement petite que μ1/2 (il faut diviser par 2 car la contrainte n'est pas que la zone verte ne doit pas rencontrer de manière indue la courbe C en bleu, mais que la zone verte ne s'intersecte pas avec elle-même) et que rm/2, les preuves précédentes garantissent l'injectivité de Γ.
Pour pouvoir effectuer le changement de variable dans le calcul du volume, il faut encore s'assurer que l'ensemble d'arrivé de Γ restreint à [a, b]xBa,ε, où ε est un nombre réel strictement positif et plus petit que μ est bien Cε. Elle est plus facile à vérifier.
-
- Surjectivité de Γ restreint à [a, b]xBa,ε dans Cε:
- Soit p un point de Cε. La fonction de C dans R, qui à un point associe sa distance à p est continue. Elle atteint son minimum en un point f(t), avec une distance inférieure à ε par hypothèse. Si h est un réel tel que t + h soit un élément de [a, b] la distance entre p et f(t+h) est plus grande que le minimum précédemment cité. On en déduit :
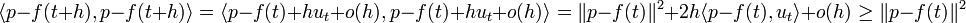
- La majoration est vraie pour les valeurs positives comme négatives de h, ce qui montre que p - f(t) est orthogonal à ut. Une autre manière de dire les choses est que p est dans l'image de Γ. Plus précisément, son antécédent est (t, φt-1(p- f(t))).
-
- Calcul du jacobien :
- Pour effectuer le changement de variable, il est utile de calculer le déterminant jacobien de ψ en un point (t, z). Pour cela calculons dans un premier temps la différentielle de ψ en ce point. Soit vt,a l'antécédent du vecteur normalisé de u't par φt, si la dérivée seconde de f n'est pas nulle et un vecteur de Ha de norme 1 et orthogonal à ua si la dérivée seconde est nulle. On note Kt,a l'hyperplan de Ha orthogonal à vt,a. On note (td, zd) un petit vecteur de Ba,μ tel que la somme du point (t, z) et de (td, zd) soit dans Ba,μ. Enfin, on utilise les notations :
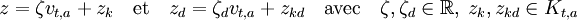
- On a :
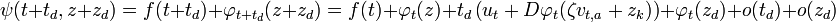
- On en déduit la différentielle :
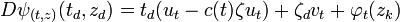
- Pour le calcul du déterminant, on remarque que la différentielle possède deux espaces stables, celui engendré par ut et vt, puis Kt,a. Sur l'espace Kt,a, la différentielle est une rotation son déterminant est égal à 1, le jacobien recherché est celui de l'espace vectoriel de dimension 2 engendré par les deux vecteurs ut et vt. Dans cette base, la matrice M est égale à :
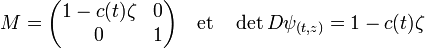
Le résultat n'est pas étonnant. Il signifie que si la courbure est localement nulle, l'application ψ ne modifie pas le volume. Le même phénomène se produit aux alentours de la courbe C. En revanche, si un petit volume est choisi avec une coordonnée ζ positive, c'est-à-dire dans la concavité de la courbure, alors le volume diminue. Il irait jusqu'à 0 si l'on se rapprochait du rayon de courbure, égal à 1/c(t), ce qui ne peut se produire avec le choix de μ, qui ne dépasse jamais la moitié du rayon de courbure. En revanche, dans la direction opposée, le volume augmente.
-
- Calcul du volume de Cε :
- On peut maintenant appliquer le changement de variable ψ :
![Vol (C_{\epsilon}) = \int_{C_{\epsilon}} 1 \mathrm d\sigma = \int_{[a,b]\times B_{\mu,a}} |\det D\varphi_{t,z}|\;\mathrm dt\mathrm d \zeta \mathrm d z_k = (b-a)\cdot Vol(B_{n-1}(\epsilon)) - \int_{[a,b]\times B_{\mu,a}} c(t)\zeta \;\mathrm dt\mathrm d \zeta \mathrm d z_k](https://static.techno-science.net/illustration/Definitions/autres/b/ba4a11263b0c003c5f0d6bd087001e23_97ac030c1e5439195736f562a6f013ab.png)
- Or le solide [a, b]x Ba,μ est symétrique par rapport à Ka et le volume de la surface coupée à l'ordonnée ζ est exactement le même que celle coupée à l'ordonnée -ζ. La deuxième intégrale est égale à 0. On trouve :
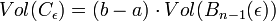
Le contenu 1 dimensionnel de la courbe C est égal à b - a, c'est-à-dire à la longueur de la courbe, car son paramétrage correspond à une abscisse curviligne. Dans le cas du cercle et en dimension 3, on retrouve une formule connue, le volume d'un tore. Dans le cas d'un courbe qui n'est pas fermé, la démonstration est exactement la même, il suffit d'ajouter les deux demi-boules aux extrémités.
Dans le cas d'une courbe, de classe C2 et admettant des points doubles, le contenu 1 dimensionnelle de Minkowski est encore égal à la longueur n'est pas très compliqué, mais l'égalité du produit précédent et du volume du tube n'est plus vérifiée. Le résultat est encore vrai pour les courbes de classe C1, les polygones ou les courbes fermées non vides compacts et convexes en dimension 2, mais les démonstrations sont différentes.
Courbe fractale
Dès 1872, Karl Weierstrass montre qu'une courbe peut avoir un comportement étrange, il construit un exemple d'arc, par définition continu, et nulle part différentiable. Plus tard, Péano construit sa courbe, dont l'image est l'ensemble des points d'un carré de côté 1. En 1904, le mathématicien suédois Koch trouve un exemple concret de courbe répondant au cahier des charges de Weierstrass, à travers un étrange flocon. Tous ces exemples correspondent à ce qui est maintenant appelé une fractale.
Cette famille de courbes, initialement considérées comme un peu pathologiques, s'avèrent essentiels pour une meilleure compréhension de certaines branches des mathématiques. L'étude d'un système dynamique comme celui de Lorenz porte sur une équation différentielle dont le comportement limite se situe à l'intérieur d'une zone géométrique définie par une telle courbe (pour être plus précis, la zone correspond à l'adhérence d'une telle courbe).
Pour l'analyse de telles courbes, un équivalent de la longueur s'avère nécessaire. Or pour la courbe de Péano, la définition différentielle n'a pas de sens et celle de Jordan donne l'infini. Si le contenu 1 dimensionnel de Minkowski donne aussi l'infini, il n'est pas très compliqué de l'adapter pour trouver une réponse qui fait sens. Si P désigne l'ensemble d'arrivé de la courbe de Péano :
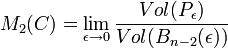
Ici, Pε désigne l'ensemble des points à distance inférieure de ε de P. L'astuce a consisté à diviser le rapport, non pas par le volume d'une boule n - 1 dimensionnel, mais n - 2 dimensionnel. Pour une nappe de classe C2 et de dimension 2, le contenu correspond à la mesure de la surface. Pour l'attracteur de Lorenz ou le flocon de Koch, aucun entier k ne permet de définir un contenu n - k dimensionnelle qui ne soit ni 0 ni l'infini. En revanche, il est possible d'utiliser une définition du volume d'une boule de dimension ζ qui fasse sens, même si ζ n'est pas un entier :
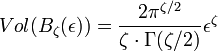
Ici Γ désigne la fonction gamma. Le contenu de Minkowski se généralise ainsi à des dimensions non entières. Cette dimension, qui permet de donner un sens à la longueur d'un arc, est appelée dimension de Hausdorff.