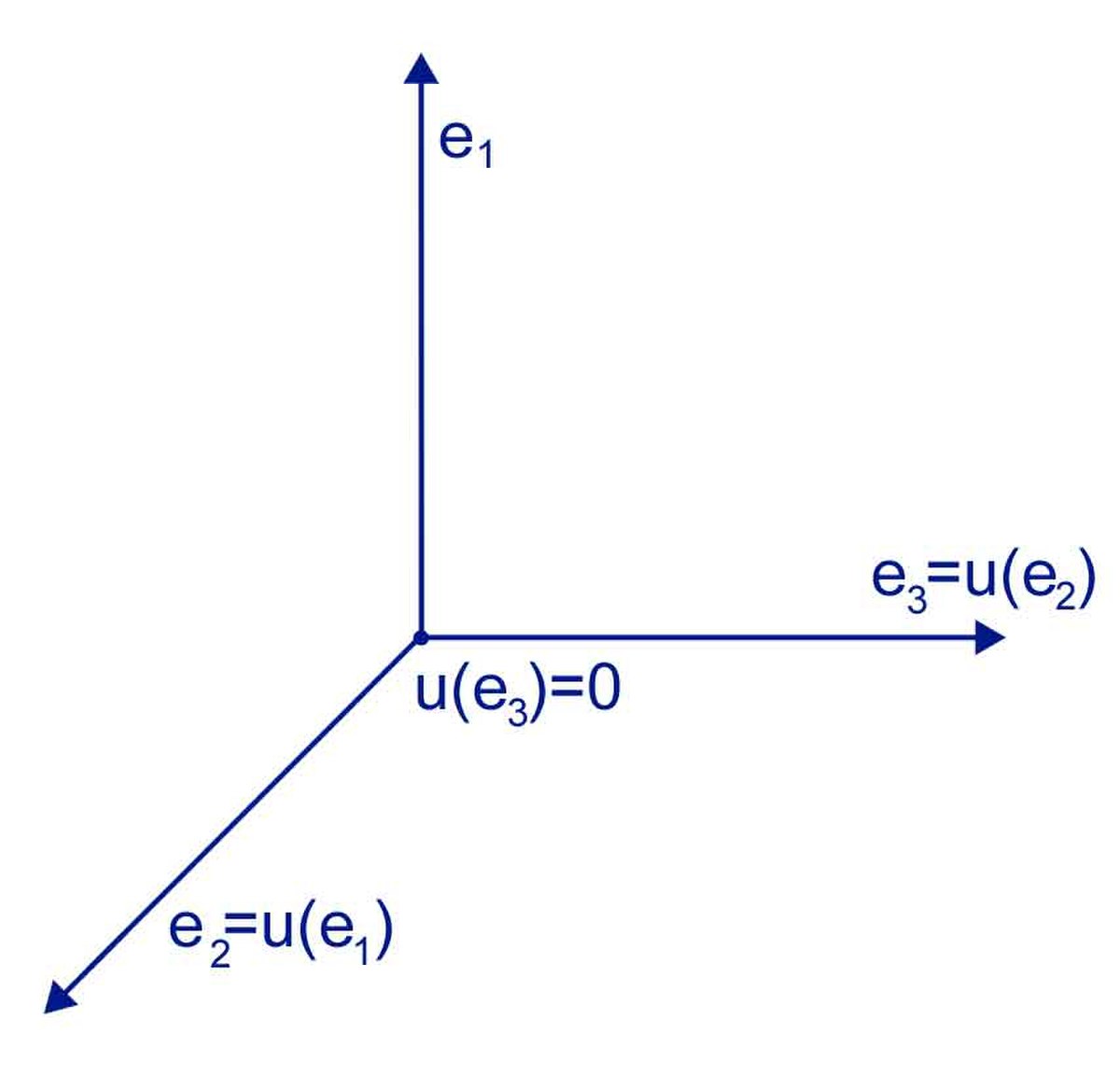
Endomorphisme nilpotent - Définition
Un endomorphisme nilpotent est un endomorphisme c’est-à-dire une application linéaire d'un espace vectoriel dans lui même, qui, composé par lui-même un nombre suffisant de fois, donne l'application nulle. Un exemple est donné dans l'illustration.
Le concept de nilpotence est important en mathématique. Il correspond à un cas particulier de diviseur de 0. On le trouve non seulement en algèbre linéaire mais aussi dans l'étude des groupe de Lie avec l'analyse des algèbres de Lie nilpotentes, mais aussi, par exemple, dans la théorie des anneaux.
En algèbre linéaire, les endomorphismes nilpotents sont importants car ils interviennent dans la réduction des endomorphismes, c’est-à-dire la représentation d'un endomorphisme quelconque sous une forme la plus simple possible. On en trouve des utilisations pratiques par exemple pour la résolution d'équations différentielles linéaires.
Un moyen de reconnaître le caractère nilpotent d'un endomorphisme est de multiplier la matrice qui le représente (dans une base de l'espace vectoriel concerné) par elle-même successivement, jusqu'à ce qu'une de ses puissances soit nulle.
Il existe un pendant à la notion d'endomorphisme nilpotent, il correspond aux matrices nilpotentes. Ces matrices offrent une approche plus concrète du concept et permettent une utilisation pratique sous la forme de calcul.
Définition
Soit
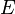
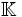
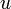
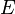
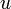
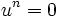
Soit x un vecteur, alors on appelle indice de x pour l'application nilpotente le plus petit entier p tel que up(x) = 0.
Intérêt du concept
Nilpotence et Réduction
Un enjeu important en mathématique est celui de la réduction, c’est-à-dire de la décomposition d'un concept en sous-concepts plus simples et qui décrivent l'intégralité du concept initial. Dans le cadre des applications linéaires la réduction est traitée dans l'article Réduction d'endomorphisme. En dimension finie, les endomorphismes nilpotents jouent un rôle important dans le cas ou
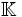
Si la clôture algébrique du corps n'est plus vraie, alors il est toujours possible d'étendre l'espace vectoriel sur un corps algébriquement clos. Cette technique est largement utilisée. Pour les réels, la physique n'utilise pratiquement uniquement que cette approche.
Applications
Puisqu'il est possible d'étendre à la clôture algébrique, la réduction des endomorphismes dans ce contexte joue un rôle essentiel en mathématique. Les endomorphismes nilpotents sont donc nécessaires à divers branches des mathématiques. En algèbre linéaire, ils interviennent naturellement dans la réduction de Jordan qui correspond à un cas important de réduction des endomorphismes. Les techniques utilisées sont celles des polynômes d'endomorphismes. Les conséquences se retrouvent sur la résolution de systèmes d'équations linéaires, dans la résolution d'équations différentielles linéaires où ils apparaissent comme des cas limite. En mathématique appliquée, ils sont importants pour la recherche d'algorithmes, on utilise alors essentiellement les matrices nilpotentes où des représentations simples sont alors nécessaires.
Propriétés
L'exemple illustre l'essentiel des propriétés des endomorphismes nilpotents. On y trouve des propriétés sur l'indice des endomorphismes et des vecteurs, des conditions nécessaires et suffisantes grâce aux polynômes. Des réductions avec une décomposition en espaces propres et l'existence d'une base réduite. Il existe aussi des propriétés calculatoires des matrices nilpotentes traitées dans l'article Matrice nilpotente.
Nilpotence et indice
L'indice d'un endomorphisme nilpotent possède deux grandes propriétés:
-
- L'indice d'un endomorphisme nilpotent est inférieur ou égal à la dimension de l'espace.
- Il existe un vecteur dont l'indice est celui de l'endomorphisme.
Nilpotence et polynômes en dimension finie
Les polynômes fournissent non seulement des conditions nécessaires et suffisantes pour la nilpotence, mais renseignent de plus sur l'indice.
-
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à
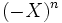
- Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à
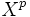
- Le polynôme annulateur d'un vecteur x est égal à
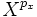
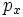
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à
Nilpotence et réduction en dimension finie
Le principe de réduction consiste à trouver une décomposition en somme directe de sous-espaces stables de l'espace vectoriel. Il en existe une pour les endomorphismes nilpotents. Et elle est compatible avec la réduction de Jordan. Cette approche est générale à l'analyse des endomorphismes. Dans le cas des endomorphismes nilpotents, elle est intimement liée à la notion de base réduite.
-
- Si
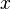
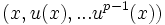
- Il existe une suite
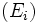
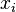
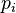
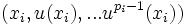
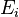
- La restriction de u à
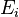
- La décomposition est maximale, c’est-à-dire qu'il n'existe pas de décomposition en sous-espaces vectoriels stables qui génèrent en somme directe l'espace entier et qui comprennent plus d'éléments que la décomposition précédente si aucun sous-espace vectoriel est réduit au vecteur nul.
- Si
Pour des raisons de simplicité des démonstrations, l'indice n'est pas celui suivi dans la présentation de l'article.
-
- Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à
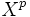
- Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à
Par définition de la nilpotence,
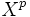
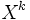
Or comme les polynômes annulateurs forment un idéal principal (voire polynôme minimal) le polynôme minimal divise donc
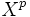
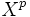
Réciproquement, dire que le polynôme minimal est égal à
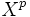
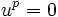
-
- Le polynôme annulateur d'un vecteur x est égal à
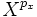
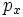
- Le polynôme annulateur d'un vecteur x est égal à
La démonstration est analogue à la précédente
-
- L'indice d'un endomorphisme nilpotent est toujours inférieur ou égal à la dimension de l'espace.
Cette proposition est une conséquence directe du résultat précédent. Le degré du polynôme minimal, égal à l'indice de l'endomorphisme, est toujours inférieur ou égal à la dimension de l'espace (voire propriété des polynômes minimaux).
-
- Il existe toujours un vecteur dont l'indice est celui de l'endomorphisme.
Cette proposition est encore une conséquence des polynômes minimaux. Il existe un vecteur dont le polynôme minimal est le polynôme minimal de l'endomorphisme. Ce vecteur est donc du même indice que l'endomorphisme.
-
- Si
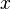
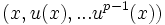
- Si
Considérons le polynôme minimal de
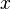
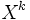
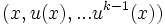
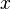
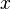
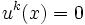
-
- Il existe une suite
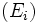
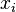
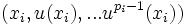
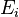
- Il existe une suite
Démontrons ce résultat sur par récurrence sur p l'indice de l'endomorphisme.
Si p est égal à 1. L'endomorphisme est nul et le résultat est trivial.
Supposons le résultat vrai pour k et démontrons le pour k+1. Soit u un endomorphisme d'indice k+1. Considérons alors la restriction de u à u(E). C'est un endomorphisme nilpotent d'indice k. Par hypothèse de récurrence, il existe une suite
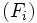
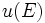
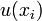
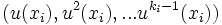
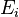
Montrons alors que la suite
![(u^j(x_i))_{i,j\in[0,k_i-1]}\;](https://static.techno-science.net/illustration/Definitions/autres/5/51811bc9045c1a9f2a4cb2ee80c3bf7c_138ebbabd5f828d046913f650e2e7297.png)
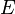
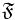
![(1)\qquad \sum_{i,j\in[0,k_i-1]} \alpha_{ij}u^j(x_i)=0\;](https://static.techno-science.net/illustration/Definitions/autres/1/11dd723291ebc8c5f7aa789d9e3486fc_e2cb7448bcf039a4b005f19e29a751ae.png)
Si nous appliquons l'endomorphisme u à cette égalité, en retranchant tout les termes nuls de la forme
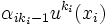
![(2)\quad \sum_{i,j\in[0,k_i-2]} \alpha_{ij}u^{j+1}(x_i)=0\;](https://static.techno-science.net/illustration/Definitions/autres/4/4131d488332c0c9d82b638defb9224a7_2d34cfc81fbd05cd779e0783920e26b2.png)
Cette combinaison linéaire est la combinaison linéaire d'une base de
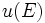
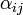
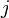
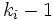
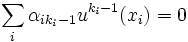
C'est une combinaison linéaire nulle d'éléments d'une base, les coefficients
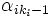
Montrons maintenant que cette famille est génératrice. Soit
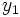
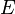
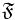
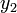
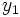
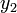
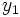
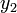
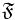
-
- La restriction de u à
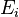
- La restriction de u à
La restriction de u à
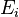
-
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à
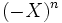
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à
La seule valeur propre est 0, donc sur sa clôture algébrique, le polynôme caractéristique est scindé et possède pour racine uniquement 0. Ce polynôme est donc une puissance de X, et de degré n. Son signe provient du signe du monôme de plus haut degré de tous les polynômes caractéristiques.
Applications en mathématiques
Matrice nilpotente
Les résultats théoriques obtenus à l'aide de l'analyse des endomorphismes nilpotents ont des conséquences importantes sur les matrices nilpotentes. Ces résultats sont traités dans l'article Matrice nilpotente.
Réduction des endomorphismes
Dans le cas où le corps est algébriquement clos et en dimension finie, les endomorphismes nilpotents jouent un rôle particulier dans la problématique de la réduction des endomorphismes. Le cas général, celui ou toutes les racines du polynôme minimal sont simples, correspond aux endomorphismes diagonalisables. Ce cas génère un ensemble d'endomorphismes partout dense. En revanche, en cas de racine multiple, alors il existe une composante nilpotente.
Cette décomposition joue un rôle important dans les calculs que l'on observe dans l'univers des matrices. Elle permet par exemple de prouver que toute matrice est trigonalisable et offre une forme particulièrement simple en bloc de Jordan.
De nombreux algorithmes relèvent directement de cette décomposition. Elle permet d'accélérer massivement la résolution d'un système d'équations linéaires.
Équation différentielle linéaire
La réduction de Jordan joue un rôle particulier pour les équations différentielles linéaires. Par exemple, dans le cas où les coefficients sont constants, alors le calcul de l'exponentielle d'une matrice dans le cas général est largement plus simple dans le cas d'une représentation matricielle réduite par la méthode de Jordan. Il est alors important de pouvoir calculer l'exponentielle d'une matrice nilpotente. Ce cas est exposé dans l'article Matrice nilpotente.
Groupes de Lie
Dans l'étude des groupes de Lie, on s'intéresse parfois à ce que l'on appelle groupes de Lie nilpotents. Comme pour tout groupe de Lie, leur structure est décrite par leur fibré tangent, qui est muni d'une structure d'algèbre de Lie. Les représentations de ces algèbres dans les endomorphismes s'obtiennent à partir d'endomorphismes nilpotents.