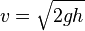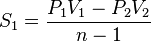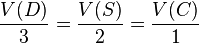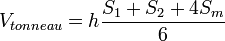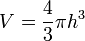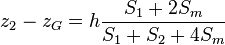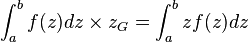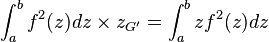Evangelista Torricelli - Définition

Evangelista Torricelli (né le 15 octobre 1608 à Faenza, en Émilie-Romagne - mort le 25 octobre 1647) est un physicien et mathématicien italien du XVIIe siècle.
Biographie
Evangelista Torricelli commença ses études dans sa ville natale, Faenza. Remarqué pour ses dons par les Jésuites, il fut envoyé à Rome. Dès 1626, il devient l'élève de Benedetto Castelli, ami fidèle de Galilée et auteur d'un travail d'hydraulique, en 1628, très au courant des travaux de Galilée. Rappelons qu'en 1632, le Dialoguo de Galilée paraît et suscite un grand émoi à Rome ; il vaut à son auteur son célèbre procès et son abjuration, le 22 juin 1633.
Torricelli disparaît alors de 1632 à 1641.
En 1641, Castelli, rendant visite à Galilée déjà aveugle, dans sa villa d'Arcetri, lui apporte un traité de Torricelli : le de Motu de 1641. À la demande de Castelli, qui s'occupe alors de la Lagune de Venise, Torricelli part à Arcetri en octobre 1641 et aidera Viviani durant les derniers mois de vie de Galilée.
Il le remplace ensuite comme mathématicien du Grand-Duc Ferdinand II de Médicis, ce qui le libère de tout souci matériel. Il est élu à l'Académie du Son (de blé), académie dont l'objectif est de purifier le langage comme on dégage le son de la mouture de blé. Cette élection le porte à examiner les arts plus que les mathématiques, ce qui lui vaut remontrances de ses amis, Bonaventura Cavalieri et les élèves de Castelli, Raffaello Magiotti et Nardi.
Torricelli est à l'acmé de sa carrière en 1644 : publication des Opera Geometrica, découverte du vide " grosso " via le baromètre à mercure.
1647 : à 39 ans, en pleine activité scientifique, la typhoïde l'emporte.
Beaucoup de ses travaux furent perdus ou publiés très tardivement, ce qui a amoindri son influence et sa renommée. On lui doit cependant :
- le " tube barométrique de Torricelli " en hydrostatique : P = ρgH
- la Formule de Torricelli en hydraulique :
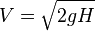
Son œuvre mathématique est pourtant considérable.
Torricelli et le baromètre (1644)
Torricelli est connu pour avoir mis en évidence, en 1644, la pression atmosphérique, en étudiant la pompe à eau de Galilée, ce qui lui permit d'inventer le baromètre à tube de mercure qui porte son nom. Une unité de pression, le torr, lui est dédiée. Elle correspond à la pression d'un millimètre de mercure. [Mais c'est le pascal qui fut retenu comme unité du système international en hommage à Blaise Pascal, qui poursuivit et développa les recherches dans ce domaine (1646-1648)].
Torricelli n'a jamais rien publié sur ce sujet, ni même revendiqué la priorité. Et Blaise Pascal, dans ses travaux, ne cite pas une fois Torricelli, mais, en 1651, déclare avoir refait en 1646-48, une expérience faite en Italie en 1644.
Il est vraisemblable que Torricelli a toujours voulu s'éloigner des démêlés avec l'Inquisition. Michelangelo Ricci lui écrit de Rome, le 18 juin 1644 : " Je crois que vous êtes déjà assez dégoûté par l'opinion inconsidérée des théologiens et par leur habitude de mêler constamment et immédiatement les choses de Dieu aux raisonnements concernant la nature. " Or les jésuites, en particulier Niccolo Zucchi, excluent le fait qu'il y ait vide dans la chambre barométrique : pour Constantini (Baliani e i Gesuiti, Firenze, 1969), c'est pour éviter un nouveau conflit avec les mathématiciens. Ceci pourrait expliquer le silence de Torricelli sur le sujet.
Origine du problème
Ce problème correspond à une considération très pratique : depuis longtemps l'approvisionnement en eau des villes a convaincu les fontainiers que les siphons dysfonctionnent à 18 brasses (soit 10,3 m). Le plâtre permettait d'élever la hauteur de la colonne d'eau, mais sans qu'on sache pourquoi.
Galilée, en 1590, est opposé à l'idée du vide " grosso ", mais sous l'influence de Jean-Baptiste Baliani concéda le vide entre molécules dans l'eau, enfin se résolut au vide " grosso " vers 1635.
Baliani en 1630 a la vision juste : La Nature n'a pas horreur du vide, seule la pression de l'air équilibre la pression de la colonne d'eau :
- P = ρgh
où P est la pression, ρ est la masse volumique du liquide en kg.m − 3, g l'attraction de la pesanteur en m.s − 2 et h hauteur en m en notation moderne. Et la pression de l'air est à évaluer par le " poids de l'air " à ses différents degré de ténuité.
En 1630, Galilée émet l'hypothèse que la cohésion de la corde d'eau est assurée par la résistance du vide intramoléculaire : trop haute, la corde casse sous son propre poids. Argumentation fausse reprise dans le Discorso. Remarque : on sait actuellement que la " pression interne de l'eau " est supérieure à 1000 bars !
Mersenne et Isaac Beeckman en discutent en 1628. Mersenne écrit à Galilée vers 1640 pour lui demander l'explication de la résistance à l'écartement de 2 lames de verre superposées.
En Italie, à Rome, Benedetto Castelli et Raffaello Magiotti décident d'étudier le problème des fontainiers ; Antonio Nardi, Gasparo Berti et Michelangelo Ricci aussi, avec le minime Emmanuel Maignan (partisan du vide grosso) et les jésuites Niccolo Zucchi et Kircher (opposés au vide grosso, pour des raisons théologiques) : Berti réussit et le montre aux Romains (avant fin 1641) : l'eau ne monte qu'à 10,3 m. Mais au-dessus, qu'y a-t-il ?
Contribution de Torricelli
Adoptant l'idée de Baliani, Torricelli a pour contribution essentielle celle de proposer le mercure de densité 13,6, qui devrait donc donner une hauteur de 10,3/13,6 = 0,76 m.
Expérience que Viviani réalise dans le courant du printemps 1644 :
- Réaliser la cuve et la remplir de vif-argent
- Prendre un ballon à long col (d'environ 1m)
- Le remplir à ras-bord
- Boucher avec le pouce et retourner sur la cuve
- Enlever le pouce
Le vif-argent s'écoule jusqu'à une hauteur de 76 cm, quel que soit le type de ballon ou son inclinaison. Par ailleurs, si de l'eau est versée sur le mercure, et qu'on retire le tube jusqu'à l'eau, celle-ci est " aspirée avec horrible violence. "
Le 11 juin 1644, Torricelli fait l'analyse critique de cette expérience avec Ricci : La nature n'a aucune horreur du vide. Le vide n'aspire pas : on peut à volonté faire coulisser le tube et réduire la chambre barométrique.
Il n'y a aucun effet sauf si on chauffe. (Il est donc, semble-t-il, impossible de réaliser un baromètre. Mais à cette époque, le verre n'était sans doute pas dégazé, et il devait s'établir une légère pression d'air dans la chambre. Peut-être aussi y restait-il de la vapeur d'eau des expériences antérieures.)
Après 1644
Mersenne tenta vainement (il faut avoir un tube de verre qui ne casse pas). Et ce furent les expériences de 1646-1648 de Petit, Florin Périer et Pascal qui résolvent magistralement le problème avec la montée au Puy de Dôme, que Mersenne ne vit pas car il meurt en 1648.
Le baromètre est né.
Qui le premier fit le calcul de la masse de l'atmosphère ? Soit la masse d'une couche de mercure de 0,76 m sur toute la surface de la Terre :
-
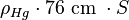
En tout cas, ce n'est pas dans les papiers de Torricelli, ni dans ceux de Baliani.
Torricelli hydraulicien, élève de Castelli
Le De Motu Aquarum fait partie du traité de 1644, Opera Geometrica, et il y est énoncé la loi de Torricelli. Sa traduction eut lieu en France, à l'intention de Fermat, en 1664, précédée de l'ouvrage de Castelli, sur les eaux courantes, et d'un discours sur la jonction des Mers. (Rappel : ce discours, qui doit dater des années 1630, il hantera Pierre-Paul Riquet (1609-1680) dès sa jeunesse.)
Torricelli est-il l'auteur de sa loi ?
est la formule qui fait connaître Torricelli dans le monde de l'hydraulique. Elle relie la vitesse v d'écoulement d'un liquide par l'orifice d'un récipient à la hauteur h de liquide contenu dans le récipient au-dessus de l'orifice, g étant l'accélération de la pesanteur.
- Antérieurement, Mersenne a écrit de nombreuses lettres à Peiresc en 1634. En 1639, il semble que Descartes le félicite pour sa loi qui calque " par anticipation " celle de Torricelli. Ces écrits sont conservés aux Arts et Métiers à Paris.
- Descartes, Mersenne, Gassendi écrivent beaucoup jusqu'en 1643 et après. Les difficultés sont bien cernées : niveau d'eau constant, perte de charge si retrécissement, problème de la buse de sortie, et bien évidemment le jet d'eau et la loi de 1638 de Galilée (4e journée). Hydraulica de Mersenne paraît en 1644 et Mersenne rencontra Torricelli en 1645. Clairement, si les vases communicants font remonter l'eau au niveau du lac, il est manifeste que le jet d'eau dirigé verticalement n'y remonte pas vraiment, et chacun voit bien ce que produit la modification de la buse dans un jet d'arrosage. La démonstration manifestement dépasse les physiciens de l'époque.
- Postérieurement, 1668, à l'Académie des Sciences de Paris, Christiaan Huygens et Jean Picard, puis Edme Mariotte reprennent le problème.
En 1695, donc après Newton (1687), Pierre Varignon raisonne ainsi :
- " La petite masse d'eau ρ.S.dx est éjectée par la force de pression S.ρ.g.h avec une quantité de mouvement ρ.S.dx.v pendant le temps dt : soit v² = g.h "
mais il y manque toujours le facteur 2.
En 1738, Daniel Bernoulli donne enfin la solution dans son Hydrodynamica. Leonhard Euler viendrait bientôt : tout deviendrait clair. Cette loi a donc fait couler beaucoup... d'eau.
Torricelli, élève de Cavalieri
Torricelli, grand admirateur de Cavalieri, dépassa le maître dans l'utilisation de la méthode des indivisibles, car pour la première fois, il va considérer des quantités homogènes : en sommant de " petites " aires, on obtient une aire, etc. La largeur des lignes vient résoudre les paradoxes de Cavalieri.
Torricelli et les indivisibles
Cavalieri est sans doute le premier à démontrer, à l'aide des indivisibles, que l’aire sous la courbe d'équation y = xn − 1 entre les points d'abscisses x1 et x2 est
-
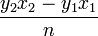
Fermat généralise cette relation pour n rationnel positif supérieur à 1 et n entier inférieur strictement à -1 en utilisant des séries.
Torricelli va généraliser le travail des indivisibles de Cavalieri à ce que la thermodynamique actuelle appelle un processus polytropique :
Soit PVn=cste,
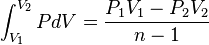
C'est le cas dit " hyperbolique " (avec n différent de 1 ; le cas n = 1 ne pourra s'obtenir qu'en utilisant les logarithmes)
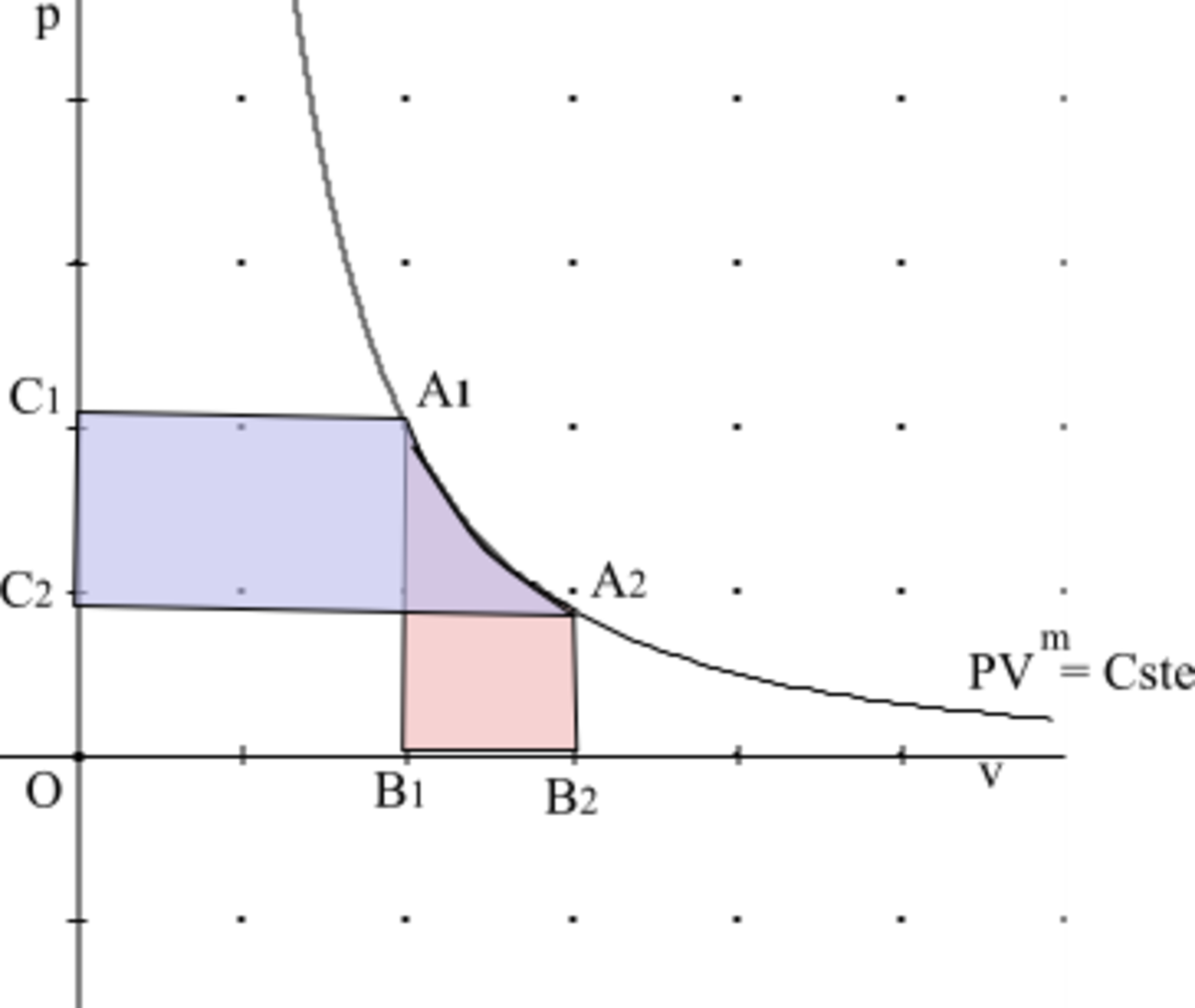
Appelons A1 et A2 les deux points sur la courbe polytropique, B1 et B2 leur abscisse ; C1 et C2 leur ordonnée. Le tour de force de Torricelli est de comparer les aires des trapèzes curvilignes S1 = aire(A1B1B2A2) et S2 = aire(A1C1C2A2). Il démontre que S2 = nS1. Ensuite il lui suffit de faire la différence des deux aires
- S1 − S2 = − (n − 1)S1
- S1 − S2 = aire(OB2A2C2) − aire(OA1C1) = P2V2 − P1V1
d'où
Pour démontrer l'égalité : S2 = nS1, Torricelli compare les aires des gnomons y.dx et x.dy. De nos jours, le calcul se fait aisément en différentiant PVn
- VndP + nPVn − 1dV = 0 d'où VdP = − nPdV
Mais le dire en 1646 reste un tour de force. Ce que vient de découvrir Torricelli, c'est que, dans cette figure infinitésimale, les aires des gnomons y.dx et x.dy sont à considérer et ce sont ces aires que l'on somme : il faut donc considérer les épaisseurs des " lignes de Cavalieri. "
Pour les volumes de révolution, il comprit aussi que les rondelles de salami ont un volume, et qu'il faut donc sommer les volumes infinitésimaux.
Il redémontre, grâce aux indivisibles, la célèbre relation d'Archimède, inscrite sur sa tombe, concernant le volume du bol (S) hémisphérique, celui du cylindre droit (D) de même rayon r et de hauteur r et celui du cône de révolution de rayon r et de hauteur r :
Il est également l'inventeur de la trompette de Gabriel, une figure géométrique qui présente la particularité étonnante de posséder une surface infinie mais un volume fini. C'est le résultat de la rotation d'une partie de l'hyperbole équilatère y=1/x, pour x>1, autour de l'axe (Ox).
Il démontre aussi la formule du volume du tonneau ou formule des trois niveaux (lettre à Roberval 1643):
- Soit un solide de révolution de méridienne une conique. Coupons-le en 2 niveaux z1 et z2. Soit z2 − z1 = h. Soit S1 l'aire du disque de cote z1, S2 celle du disque de cote z2, Sm l'aire du disque de cote moyenne
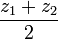
-
Il en déduit le volume du rond de serviette :
- Soit une sphère de rayon R. Ôter par perçage le cylindre, centré, vertical, de base circulaire, ce qui ne laisse qu'un volume annulaire, appelé vulgairement " rond de serviette ", de hauteur 2h.
-
Ce volume se calcule en ôtant au volume du tonneau de hauteur 2h le cylindre de rayon
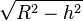
Calcul des barycentres
Torricelli s'intéresse aussi au barycentre des solides étudiés. Ainsi, dans la même lettre adressée à Roberval, précise-t-il la position du centre de gravité du tonneau :
- Soit un solide de révolution de méridienne une conique. Coupons-le en deux niveaux z1 et z2 et notons h = z2 − z1. Soit S1 l'aire du disque de cote z1, S2 celle du disque de cote z2, Sm l'aire du disque de cote moyenne
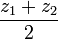
-
Enfin, généralisant une coupe de pierre en biseau que lui avait proposée Cavalieri, il publie le 7 avril 1646, la formule pour le centre de gravité (réécrite en notation moderne) :
- Soit x = f(z) l'équation de la méridienne d'une surface de révolution, limitée par les plans z = a et z = b. Alors le barycentre de la surface méridienne a pour cote zG vérifiant
-
- Et le barycentre G' du volume a pour cote zG' vérifiant
-
Torricelli avait-il connu les théorèmes de Guldin de 1643 ? En tout cas, leurs recherches se complétaient.
Torricelli cinématicien, élève de Galilée
La cycloïde
Admirateur de Galilée, élève doué de Cavalieri, il va poursuivre des idées qui existaient déjà chez Roberval.
Jean Itard (historien du Centre Koyré, Paris) a minutieusement mené l'enquête au sujet de la quadrature de la cycloïde :
Galilée aurait répondu qu'il avait vainement cherché, y compris en découpant un patron en carton et en le pesant. La compétition Roberval-Torricelli est plus serrée, et il est difficile d'y voir clair, car à l'époque, on déclarait avoir trouvé, mais on ne publiait pas, de peur que l'autre vous double : les questions de priorité seront le cauchemar du XVIIe.
Mais le résultat de l'enquête est là : priorité à Roberval, sans méconnaître les mérites de Torricelli.cf. cycloïde.
Diagramme horaire
En revanche, il est vraiment l'inventeur du diagramme horaire et du diagramme des espaces : il dit très clairement en toute généralité, puis sur des exemples simples, que si la vitesse du mobile est v(t), son abscisse sera
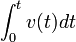
Et réciproquement, Torricelli parle du " théorème d'inversion ": si on possède x(t), la " tangente " donnera la vitesse :
-
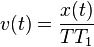
où TT1 est la sous-tangente, T est le point de l'axe des abscisses d'abscisse t, T1 est le point d'intersection de la tangente à la courbe au point d'abscisse t avec l'axe des abscisses.
Il en est donc au même niveau que Barrow en Angleterre. En tout cas, James Gregory, élève à Bologne, avec les continuateurs de l'œuvre de Cavalieri, sut en profiter.
Diagramme des espaces : la formule
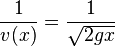
Parabole de sûreté
- Voir article détailé : Parabole de sûreté
C'est lui qui, pour la première fois invente la notion d'enveloppe, et trouve la solution complète de la chute libre " avec violence ", et la description complète de la parabole de sûreté, via une méthode peu connue.
Malheureusement, il ne compléta pas son travail : sans introduction de la résistance de l'air, la notion d'asymptote (cf. balistique extérieure) n'existe pas ; et son travail est la risée des artilleurs (les bombardieri).
Coordonnées polaires
Par ailleurs, par sa méthode des indivisibles courbes, il va pouvoir traiter les problèmes de courbes en coordonnées polaires, à une époque où Descartes venait tout juste de parler de coordonnées cartésiennes : il sait intégrer l'aire et la longueur des spirales r = θk ; mais surtout, il va découvrir la cochlée (cf. spirale logarithmique) et ses propriétés extraordinaires (Opere, III, p 368, p 477, Lettres à Ricci de 1646 et à Cavalieri(1598-1647)):
Soit une spirale logarithmique, l'arc issu de M s'enroule une infinité de fois autour de O mais sa mesure est finie : tracer la tangente en M. Y placer le point C de manière que le triangle OCM soit isocèle.
L'arc mesure OC+ CM.
L'aire balayée par OM est égale à l'aire du triangle OCM.
Bernoulli n'aurait pas dit mieux.
Torricelli, dynamicien ?
Il est encore bien tôt, avant 1647, de parler de dynamique. Néanmoins, quelqu'un étudiant la proto-dynamique serait certainement intéressé par l'évolution du concept de percussion depuis Galilée vers 1590 jusqu'aux leçons de Torricelli en 1644-1646 à l'Academia del Crusco. Un spécialiste y trouverait des phrases troublantes du type :
" La gravité est une fontaine d'où jaillissent continuellement des quantités de mouvement... Elles se conserveront et s'agrègeront ; quand le grave vient donner la percussion sur le marbre, il n'applique plus sa charge de 100 livres, fille d'un seul instant, mais les forces omnes(sommées) filles de dix instants. "
Si on remplaçait le mot instant par durée, ce texte serait d'une incroyable modernité.
Tragique destin
Le 5 octobre 1647, il écrivit à Cavalieri : " Je vais écrire un livre sur " des lignes nouvelles ". " Le 25, une typhoïde l'emportait. Et Cavalieri meurt peu après. Qui récupère ce " fatras d'idées " ? Une cassette, la fameuse cassette, léguée à Serenai ? Cette cassette contiendrait aussi la recette de fabrication de très bons verres d'optique : Torricelli en était un des maîtres.
John Wallis et Jacques Bernoulli se seraient régalés d'un tel trésor. Les recherches de filiation seront sans doute à chercher, soit vers l'école des Minimes (Mersenne ?), soit vers Stefano degli Angeli et son élève James Gregory, mais il est clair que cette mort prématurée et le travail de l'Inquisition vont affaiblir l'école italienne. Florence resta active ; néanmoins la flamme va passer dans une Angleterre florissante (Gregory, Wallis, Barrow), alors que Venise doit compter ses sous, pour sa guerre contre les Ottomans, et que l'Allemagne vient d'être ravagée par la guerre de Trente Ans (1618-1648).
Si héritage et continuation il y a, c'est peut-être chez Christiaan Huygens (1629-1695) qu'il faut chercher. Adolescent comblé (il est le fils de Constantijn Huygens, premier ministre de Hollande), il reçut de Mersenne, qui le connaissait via Descartes, maints problèmes transmis par Torricelli, qui lui servirent d'apprentissage dès l'âge de 16 ans (1645).