Claude Shannon - Définition
| Nom : | Claude Elwood Shannon |
|---|---|
| Naissance : | 30 avril 1916 Gaylord, Michigan, États-Unis |
| Décès : | 24 février 2001 (à 84 ans) |
| Nationalité : |
|
| Profession : | Ingénieur, Chercheur |
| Remarques : | père fondateur, de la théorie de l'information |
Claude Elwood Shannon (30 avril 1916 à Gaylord, Michigan - 24 février 2001) est un ingénieur électricien et mathématicien américain. Il est l'un des pères, si ce n'est le père fondateur, de la théorie de l'information. Son nom est attaché à un célèbre " schéma de Shannon " très utilisé en sciences humaines, qu'il a constamment désavoué.
Biographie
Il étudie le génie électrique et les mathématiques à l'Université du Michigan en 1932. Il utilise notamment l'algèbre booléenne pour sa maîtrise soutenue en 1938 au Massachusetts Institute of Technology (MIT). Il y explique comment construire des machines à relais en utilisant l'algèbre de Boole pour décrire l'état des relais (1 : fermé, 0 : ouvert).
Shannon travaille vingt ans au MIT, de 1958 à 1978. Parallèlement à ses activités académiques, il travaille aussi aux laboratoires Bell de 1941 à 1972.
Claude Shannon est connu non seulement pour ses travaux dans les télécommunications, mais aussi pour l'étendue et l'originalité de ses hobbies, comme la jonglerie, la pratique du monocycle et l'invention de machines farfelues : une souris mécanique sachant trouver son chemin dans un labyrinthe, un robot jongleur, un joueur d'échecs (roi tour contre roi), etc. L'un de ces "gadgets" présente toutefois un grand intérêt conceptuel, comme le montrent Philippe Boulanger et Alain Cohen dans Le Trésor des paradoxes (Éditions Belin, 2007) : "Claude Shannon voulut élaborer une " machine gratuite ", sans finalité : on la met en marche en appuyant, comme sur tout dispositif électromécanique, sur une touche " on " ; mais les choses prennent alors une tournure surprenante, car cette mise sous tension déclenche un mécanisme provoquant aussitôt l’arrêt du gadget en mettant l’interrupteur sur " off ! " Ce type de comportement insolite caractérise les situations ubiquitaires où la communication réside paradoxalement dans l'absence de communication, l'utilité dans l'absence d'utilité. Exemples : "La mode, c'est ce qui se démode" (Jean Cocteau); "Créer cette École (L’École Freudienne) afin de la dissoudre" (Jacques Lacan); "On se rend compte que l'on dort en se réveillant" (John Lennon); "Le bon fonctionnement de tout le système de l’épargne-logement suppose, paradoxalement, que certains ayants droit (les " bons frères ") renoncent précisément à faire valoir leur droit à un prêt au terme d’une période d’épargne" (Pierre Chaillol); "L'idéal révolutionnaire n’a pu que se troubler au moment de s’accomplir : la nécessité dont il se réclamait le condamnait à se perdre pour se réaliser, trahi et déformé moins par ses ennemis que par ceux-là mêmes qui ont voulu en assurer l’application" (Jean Starobinsky); "La virginité se perd en se prouvant" (Fernand Crommelynck). Un avatar géostratégique de cet automate paradoxal de Shannon consiste dans le concept de dissuasion nucléaire: les puissances nucléaires amassent des armes atomiques dans le but... d'interdire toute velléité d'emploi de ce type d'armes, en se neutralisant mutuellement: ça sert à ne pas servir!
Souffrant de la maladie d'Alzheimer dans les dernières années de sa vie, Claude Shannon est mort à 84 ans le 24 février 2001.
Son œuvre
Pendant la Seconde Guerre mondiale, Shannon travaille pour les services secrets de l'armée, en cryptographie, chargé de localiser de manière automatique dans le code ennemi les parties signifiantes cachées au milieu du brouillage. Son travail est exposé dans un rapport secret (déclassifié dans les années 1980 seulement), qui donne naissance après-guerre à un article, A Mathematical Theory of Communications (1948), qui fut repris en 1949 sous forme de livre avec un ajout de Warren Weaver, son supérieur dans les services secrets. Cet ouvrage est centré autour de la problématique de la transmission du signal.
Le schéma de Shannon
Pour décrire la communication entre machines, l'article de 1948 et le livre de 1949 commencent tous deux par un " schéma " qui connut dès lors une postérité étonnante en Sciences de l'information et de la communication, au point que Shannon s'en étonna et s'en dissocia. Le schéma modélise la communication entre machines en 5 éléments :
Ce schéma est la traduction " civile " d'un schéma préalable, utilisé dans le contexte militaire :
- source --> encodeur --> signal --> décodeur --> destinataire, dans un contexte de brouillage.
Adéquat à décrire la communication entre machines, ce schéma ne modélise qu'imparfaitement la communication humaine[réf. nécessaire]. Pourtant, son succès est foudroyant, et il a participé largement à la création d'un champ disciplinaire, les sciences de l'information et de la communication. L'une des explications de ce succès est le fait qu'il se fond parfaitement dans une approche béhavioriste des médias. De plus, ce schéma dit canonique donne une consistance et une apparence de scientificité.
Shannon : l'unité de mesure
Dans l'article comme dans le livre, il popularise l'utilisation du mot bit qui mesure l'unité élémentaire d'information numérique, bien qu'il n'en soit pas l'inventeur (John Tukey fut le premier à utiliser le terme).
Le bit est une unité de mesure désignant le nombre de chiffres binaires nécessaires pour coder une quantité d'information.
Pour coder 2 états (pile ou face), 1 Shannon (ou 1 bit) est nécessaire : 0 ou 1
Pour coder 4 états, on doit utiliser 2 Shannon (2 bits) : 00, 01, 10, 11.
5 bits minimum sont indispensable pour coder les 26 lettres de l'alphabet, car :
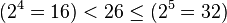
Plus généralement, soit P le nombre d'états possibles, n le nombre de bits :
P = 2n
n = log2(P)
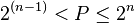
La relation de Shannon
Dans le domaine des télécommunications, la relation de Shannon permet de calculer la valence (ou nombre maximal d'états) en milieu perturbé :
Soit S le signal, N le bruit :
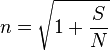
On a alors le débit maximal :
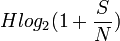
Ce résultat est indépendant de la vitesse d'échantillonnage et du nombre de niveau d'un échantillon (la valence).
Entropie au sens de Shannon
Un apport essentiel des travaux de Shannon concerne la notion d'entropie. Si l'on considère N événements de probabilité p1, p2... pN, indépendants les uns des autres, alors leur entropie de Shannon est définie comme :
Entropie =
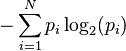
Il a par ailleurs :
- établi un rapport entre augmentation d'entropie et gain d'information ;
- montré l'équivalence de cette notion avec l’ entropie de Ludwig Boltzmann en thermodynamique.
La découverte du concept ouvrait ainsi la voie aux méthodes dites d'entropie maximale (voir probabilité), donc au scanner médical, à la reconnaissance automatique des caractères et à l'apprentissage automatique .
Anecdotes
- En 1981, Claude Shannon a commencé à écrire un article intitulé Scientific Aspects of Juggling, sur l'art de la jonglerie. Cet article était prévu pour être publié dans Scientific American, mais ce ne fut finalement pas le cas. Néanmoins, cette ébauche a servi de base à la formalisation des mouvements de jonglerie par le siteswap.[1]


















































