Histoire des polynômes - Définition

L'histoire des polynômes se confond avec celle de l'algèbre et celle de la résolution d'équations. Ils sont les outils privilégiés utilisés pour résoudre les problèmes tels que la résolubilité des équations, la constructibilité et le dernier théorème de Fermat.

Les fondements

Les mathématiques grecques sont essentiellement arithmétiques et géométriques. Les résolutions d'équations se font pratiquement sans symbolisme et avec une référence fréquente à l'aspect géométrique. On voit apparaître chez Diophante (250) un début d'écriture algébrique : l'inconnue y est nommé Le Nombre et une lettre ξ lui est attribuée.

Durant leur séjour chez les mathématiciens de langue arabe, les mathématiques se détachent progressivement de la contrainte géométrique. C'est la naissance de l'algèbre que l'on attribue traditionnellement à al-Khawarizmi dans son ouvrage Abrégé du calcul par restauration et comparaison. Il y décrit et résout les 6 équations canoniques du second degré ainsi que les méthodes pour s'y ramener. Il y distingue: la racine (X) , le carré (X²) et le nombre seul. Avec les travaux d'Abu Kamil, les calculs ne se font plus à l'aide seulement de rationnels mais les nombres réels positifs y prennent toute leur place. On voit apparaître alors une généralisation des opérations qui ne vont plus s'appliquer seulement aux nombres mais aussi aux inconnues. L'étude des équations se poursuit avec celle des équations cubiques chez Omar Khayyam et Din al-Tusi ( XIII ^e siècle). Dans les ouvrages d'Ibn al-Banna (1321), les polynômes de degré n sont représentés par la suite de leurs coefficients. La contrainte d'une homogénéité géométrique (X est une longueur, X² est une aire) disparait. Les raisonnements se font presque entièrement dans le domaine de l'algèbre.

En Europe, la recherche d'une symbolique se développe. Michael Stifel (1487-1567) utilise une inconnue privilégiée qu'il répète autant de fois qu'il le faut pour indiquer le degré. Cohabitent à cette époque, plusieurs symboles pour le plus (p ou +) et le - (m ou -) et le = (=, [ , S). En 1484, Nicolas Chuquet invente l'exposant : l'inconnue à la puissance 5 s'écrira I⁵. Cette notation sera reprise par Bombelli, Simon Stevin et Descartes. Viète (1540-1603) développe le calcul littéral, représente les inconnues par des voyelles et les paramètres par des consonnes et introduit les notations de la somme, du produit, du quotient, et de la puissance : B in A quadratum, plus D in A, aequari C se traduit ensuite par Descartes en bx² + dx = c. Tout est alors en place pour que se développe l'étude générale des polynômes.

Théorème fondamental de l'algèbre

Dès cette époque, on cherche à découvrir les relations existant entre un polynôme et ses racines (nombres, formes, etc.). Viète met en évidence les relations existant entre les coefficients d'un polynôme et ses racines.

Le nombre de racines d'un polynôme pose problème. Les racines sont d'abord cherchées parmi les réels positifs puis parmi tous les réels. L'invention des nombres complexes par Bombelli (vers 1572) va permettre de trouver des racines à toute équation_du_second_degré. La question suivante se pose alors : un polynôme de degré n possède-t-il toujours n racines ? René Descartes l'affirme sans le prouver. Bombelli, formalisant le calcul sur les complexes, met en évidence l'écriture pour les racines d'un polynôme. Jean Le Rond d'Alembert prouve en 1746 que toutes les racines doivent avoir la forme précédente. Cependant, il faut attendre Carl Friedrich Gauss (1777- 1855) et une incursion dans le domaine de l'analyse et la topologie pour prouver que tout polynôme de degré n à coefficients dans possède exactement n racines dans . C'est le théorème de d'Alembert-Gauss ou théorème fondamental de l'algèbre.

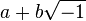
Résolution générale des équations de degré n

On pourrait croire que le théorème d'existence des racines achève l'étude des polynômes. Cependant, un problème persiste : quelles méthodes peut-on employer pour les trouver? La résolution de l'équation du second degré, puis celle du troisième degré avec les formules de Cardan-Tartaglia (milieu du XVI^e) laisse présager qu'une méthode générale existe. Les équations du quatrième degré tombent grâce à Ludovico Ferrari (1522-1565). Reste le grand champ des équations de degré supérieur ou égal à 5. Des tentatives de changement de variables, pour se ramener à des degrés moindres sont menées en particulier par Walter von Tschirnhaus (en 1689), Leonhard Euler et Étienne Bézout.

Cependant, c'est dans une autre direction que la solution sera trouvée. Déjà, des résultats intéressants étaient connus sur racines et coefficients : les coefficients s'expriment, en fonction des racines, sous forme de polynômes symétriques. En 1770, Alexandre-Théophile Vandermonde étudie les permutations des racines dans l'expression des coefficients. C'est la naissance d'une nouvelle branche de l'algèbre : l'étude des permutations qui conduira Évariste Galois à construire la notion de groupe de permutations et de groupe en général. On peut citer dans cette voie les études de Paolo Ruffini, en 1813 et celle d'Abel en 1824 et 1826. Mais c'est à Évariste Galois que revient l'honneur de faire tomber la conjecture. Les équations de degré 5 et au-delà ne sont pas toujours résolubles par radicaux.

Nombres algébriques

La connaissances des polynômes à coefficients dans semble être complète. Mais qu'en est-il des polynômes à coefficients dans ? Quels sont les réels ou les complexes qui peuvent être exprimés comme solution d'une équation de degré n à coefficients entiers ? L'étude des nombres algébriques est née, dominée par deux problèmes célèbres: celui des nombres constructibles à la règle et au compas et celui du dernier théorème de Fermat.

La question des nombres constructibles à la règle et au compas est un problème qui préoccupe les mathématiciens depuis l'époque d'Euclide. Quatre questions résistent encore au XVIII^e siècle : la trisection de l'angle, la duplication du cube, la quadrature du cercle et la constructibilité des polygones réguliers. C'est par le biais des polynômes et des extensions quadratiques (partant des nombres rationnels, on agrandit progressivement l'ensemble en y ajoutant des solutions d'équations du second degré à coefficients dans , puis à coefficients dans l'ensemble que l'on vient de créer et ainsi de suite) que la solution sera trouvée. Gauss décrit les polygones constructibles (Théorème de Gauss-Wantzel) et Pierre-Laurent Wantzel fait tomber les deux autres conjectures (la quadrature du cercle résistera quelques temps) et termine la démonstration de Gauss.

Le dernier théorème ou conjecture de Fermat - existe-t'il des solutions entières à une équation du type xⁿ+ yⁿ = zⁿ pour des degrés autres que 1 et 2 ?- nargue les mathématiciens depuis le XVII^e siècle. Nombreux sont ceux qui vont tenter de la résoudre par l'algèbre. Euler s'y casse les dents. L'école allemande de la fin du XIX^e siècle avec Richard Dedekind, Ernst Kummer, David Hilbert, Emmy Noether va développer et approfondir le travail sur les polynômes, construisant la notion d'anneau, d'idéal, de corps, de nombres algébriques sans pour autant résoudre le problème. Cependant, il font ainsi faire aux mathématiques algébriques un saut considérable.

On peut à juste titre dire que les problèmes précédents, moteur des recherches sur les polynômes, ont contribué à la naissance et développement de l'algèbre générale.

Sources

• Une histoire de la science arabe Ahmed Djebbar
• Histoire des mathématiques Jacques Bouveresse, Jean Itard, Émile Salé
• Le dernier théorème de Fermat Simon Singh