Anneau noethérien - Définition

Classe des anneaux noethériens

La plupart des opérations algébriques conservent la noethérianité. Rappelons et complétons les exemples ci-dessus :

• les corps et les anneaux principaux sont noethériens ;
• tout quotient et produit direct fini d'anneaux noethériens est noethérien ;
• tout anneau de polynômes à un nombre fini d'indéterminées sur un anneau noethérien est noethérien. Ainsi toute algèbre de type fini sur un anneau noethérien est noethérienne ;
• tout localisé d'un anneau noethérien est noethérien ; plus généralement, si M est un A-module noethérien, tout localisé S^-1M est un S^-1A-module noethérien. (En effet, pour tout sous-module N de S^-1M, on a N = (S^-1A)(N ∩ M) ; on en déduit que toute suite croissante (N_n) de sous-modules de S^-1M est stationnaire, puisque la suite (N_n ∩ M) l'est.)
• le complété formel (en) d'un anneau commutatif noethérien pour la topologique I-adique (I un idéal de A) est noethérien ;
• Si un anneau noethérien est fini sur un sous-anneau (c'est-à-dire qu'il est de type fini comme module sur le sous-anneau), alors ce dernier est noethérien (Théorème d'Eakin) ;
• tout anneau est réunion croissante de sous-anneaux noethériens.

Par contre, en général,

• un sous-anneau d'un anneau noethérien n'est pas noethérien (par exemple l'anneau de polynômes à une infinité d'indéterminées à coefficients dans un corps n'est pas noethérien, mais c'est un sous-anneau de son corps des fractions qui est noethérien);
• un produit tensoriel d'anneaux noethériens n'est pas noethérien (prendre L le corps des fractions rationnelles à une infinité d'indéterminées à coefficients dans un corps K et considérer le produit tensoriel . Ce dernier n'est pas noethérien, alors que K et L le sont).

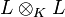
Exemples

Premiers cas

Tout corps est manifestement noethérien, par absence d'idéaux non triviaux. Tout anneau principal est aussi noethérien car chaque idéal est engendré par un unique élément, ainsi Z, K[X] l'anneau des polynômes à coefficients dans un corps est noethérien. En revanche, lorsque c'est possible, il est plus simple de les étudier à l'aide d'une division euclidienne ou, ce qui est toujours possible, d'utiliser le théorème fondamental de l'arithmétique dans le cadre d'un anneau factoriel.

Tout anneau fini est noethérien, on trouve leur présence, par exemple dans le cadre de la géométrie algébrique ou de la théorie algébrique des nombres.

Polynômes et séries formelles

Un anneau de polynômes n'est pas toujours principal, Z[X] est un exemple déjà cité. Un anneau de polynôme en plusieurs indéterminées Q[X, Y] n'est pas non plus principal, l'idéal des polynômes de degré supérieurs ou égal à 1 nécessite deux générateurs, les indéterminées X et Y.

Le théorème suivant, découvert par David Hilbert en 1888 est parfois nommé Théorème de la base de Hilbert :

• Soit A un anneau commutatif noethérien, l'anneau de polynômes A[X] est noethérien.

Il se généralise aisément (par récurrence) au cas de plusieurs indéterminées :

• Soient A un anneau commutatif noethérien et n un entier naturel, l'anneau de polynômes A[X₁, ...,X_n] est noethérien.

En revanche, un anneau de polynômes sur un nombre infini d'indéterminées n'est jamais noethérien (quel que soit l'anneau de coefficients) : la suite d'idéaux dont le n^ième est engendré par (X₁, ...,X_n) est croissante mais non stationnaire.

Comme exemple d'utilisation, on peut imaginer en géométrie une surface algébrique S définie comme l'ensemble des racines d'une famille infinie de polynômes à plusieurs indéterminées et sur un anneau noethérien. Le théorème de la base de Hilbert indique qu'il suffit de considérer une famille finie de polynômes pour définir S. En effet, l'ensemble des polynômes s'annulant sur S forme un idéal.

Soit J un idéal quelconque de A[X] ; l'objectif est de montrer que J est de type fini, ce qui prouvera que A[X] est noethérien.

Soit (D_n) la suite d'idéaux de A définie par :

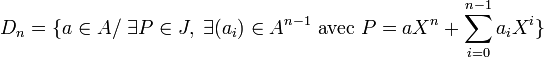
Cette suite (D_n) est croissante (car ) donc constante à partir d'un rang r (car A est noethérien). La réunion de tous les D_n est donc égale à D_r.

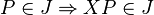
Pour chaque entier n, l'idéal D_n est de type fini (car A est noethérien) donc possède une famille génératrice finie (a_n,i) (le second indice,i, parcourt un ensemble fini I_n). Pour chacun de ces a_n,i, soit P_n,i un polynôme de J de degré n et de coefficient dominant égal à a_n,i.

Montrons que la famille finie (P_n,i), doublement indexée par n inférieur ou égal à r et par i dans I_n, engendre J. Cette assertion signifie que tout polynôme Q de J s'exprime comme combinaison linéaire à coefficients dans A[X] de cette famille (P_n,i).

Si Q est nul, c'est immédiat. Sinon, on se ramène à ce cas par récurrence sur le degré d de Q : supposons que la famille engendre tous les polynômes de J de degré strictement inférieur à l'entier naturel d (pour d=0 c'est acquis, le seul polynôme de degré < 0 étant le polynôme nul). Soient q le coefficient dominant de Q et s=min(r,d). Alors q appartient à D_d=D_s. Il existe en conséquence une famille (μ_i) d'éléments de A telle que

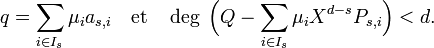
L'hypothèse de récurrence montre que Q est engendré par la famille (P_n,i), ce qui termine la démonstration.

Par un argument similaire (portant sur les coefficients non nuls de plus bas degré au lieu des coefficients dominants), on démontre le théorème suivant (qui se généralise de même à plusieurs indéterminées) :

• Soit A un anneau commutatif noethérien, l'anneau de séries formelles A[[X]] est noethérien.

Anneau d'entiers

Plusieurs exemples d'anneaux noethériens proviennent de l'arithmétique via l'étude d'équations diophantiennes, même si leur utilisation dépasse maintenant largement ce cadre. Un exemple simple est donné par le théorème des deux carrés de Fermat, qui fait intervenir l'anneau des entiers de Gauss. C'est un cas particulier d'anneau d'entiers quadratiques. Ce sont tous des anneaux de Dedekind, en particulier ils sont noethériens. Plus généralement :

Soient

A un anneau commutatif intègre,

K son corps des fractions,

L une extension finie séparable de K, et

B l'anneau des éléments de L entiers sur A.

Si A est noethérien et intégralement clos alors B est un A-module de type fini.

(L'article Élément entier montre que B est un anneau. Clairement, il contient A et il est commutatif unitaire et intègre.) Remarquons que d'après cet énoncé, B est noethérien à la fois en tant que A-module et en tant qu'anneau.

Ce résultat est lourd de conséquences, par exemple en théorie algébrique des nombres. La démonstration proposée ici utilise un outil appelé forme trace, utilisé aussi pour définir le discriminant d'un anneau d'entiers algébriques. Une démonstration plus simple est proposée dans le cas particulier des entiers quadratiques dans l'article Idéal de l'anneau des entiers d'un corps quadratique.

Notons n = [L:K] le degré de l'extension ; l'objectif est de montrer que B est isomorphe à un sous-module de Aⁿ.

Dans un premier temps, remarquons que B contient un sous-module isomorphe à Aⁿ. En effet, le théorème de l'élément primitif montre l'existence d'un élément x de L tel que L soit égal à K[x]. Il existe même un élément y de B tel que L=K[y], car x est algébrique sur K donc est solution d'une équation de degré n de la forme

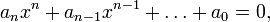
où les a_i appartiennent à K ou même (quitte à les multiplier par le produit de leurs dénominateurs) à A. L'élément y = a_nx est alors entier sur A, puisque

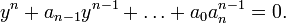
Ainsi, le A-module A[y] est inclus dans B et est isomorphe à Aⁿ.

Soit <.,.>_L/K la forme trace de L sur K, c'est-à-dire la forme bilinéaire symétrique sur le K-espace vectoriel L, qui à deux éléments de L associe la trace de l'endomorphisme de multiplication par  :

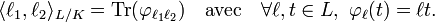
• L'extension est séparable, la forme trace est en conséquence non dégénérée (cette propriété est démontrée dans l'article Forme trace).
• De plus,

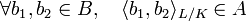
(car si l'élément b=b₁b₂ est entier sur A alors ses conjugués aussi donc la trace de φ_b aussi, donc elle appartient à A puisque A est supposé intégralement clos).

D'après ces deux propriétés, l'application ψ définie par

est un morphisme injectif de A-modules, de B dans le dual de A[y] (ce dual est l'ensemble des formes linéaires du A-module A[y]). Or le A-module A[y] est isomorphe à Aⁿ, donc son dual aussi.

On en déduit que le A-module B est isomorphe à un sous-module de Aⁿ, lequel est noethérien puisque A l'est. Ainsi, B est de type fini.